略谈现代逻辑的起点：命题逻辑

万尤栋

公元前4世纪，亚里士多德集古希腊逻辑学之大成创立的古典二值、词项逻辑已达到相当完善的程度，后来为麦加拉和斯多葛学派发展的命题逻辑和蕴涵式研究，则可视为现代逻辑的一个起点。至1847年布尔首先实现代数与传统形式逻辑的结合而命题演算出现，1879年弗雷格建立第一个谓词演算系统后，现代逻辑把两个演算造成系统，使推理的严密性、科学性和复杂性达到传统逻辑无可比拟的程度；而20世纪30年代德国G.甘岑提出的自然推理，则不从给定的公理出发，却能精确地把日常推论转化为逻辑结构。由此可知，把握源头，深入研究命题逻辑，是把握现代逻辑科学的必经途径。

作为推理基本要素的命题，是具有真值的语句，其在二值逻辑中具有唯一的真值。对于建立在简单命题基础上的命题逻辑（演算），似应着重把握：一是命题形式。包括：1.命题的符号化。通过“¬、∧、∨、→、↔”等语句联结词，把简单命题结合成复合命题。命题逻辑规定，具有一定结构形式的穷长符号串（可以空）称为命题形式或合式公式。2.通过命题形式，确定命题与其常项（特指）或变项（非特指，通常以p、q、r，…，或p ₁ ，p ₂ ，p ₃ ，…，p _n …表示）间的逻辑关系：由n个不同变项组成的复合命题可共有2 ⁿ 种不同的赋值，而一个命题形式若对每一种真值指派都为真，则称重言式；都为假，则称矛盾式；若至少有一种真值指派为真，则称可满足的。3.等值演算。即对变项的每一组真值指派，都使给定的两个命题形式A与B的值相等，则A B（为元语言符号式即表示对象语言的等价式A↔B，类似的还有 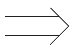表示→以作区别）。命题逻辑对一些反映逻辑规律的重要定律以等值形式给出（共20式），其通常也是布尔（逻辑）代数的主要组成部分。如第（18）式为“等价（律）”，（p↔q） （p → q）∧（q → p）。4.范式。除真值表方法外，可用求范式的方法比较两个命题形式，或确定一命题形式的类型是重言式，或矛盾式，或是可满足的。二是推理规则。包括自然推理规则和公理系统L的推理规则。

自然推理，可从任意给定的前提出发，依据推理规律，用给定的推理规则或图式进行推理。举其要义：一、重言蕴涵式。当且仅当（A ₁ ∧ A ₂ ∧…∧ Ak）→ B（K ≥ 1），为重言式时，则称命题B为前提A1，A2…，Ak的逻辑结论。常用以描述正确的推理形式而一般称之为推理定律的有9个重言蕴涵式，加上前述20个重要等值式根据第（18）式等价关系式可各自分解为两个蕴涵式（共40式），其也都是重言式，都可作为公共的前提用在任意证明之中。二、所谓证明，乃是描述从前提推得结论的过程，是一个有内在联系的命题形式序列。构造严谨逻辑结构的证明，不仅要按推理定律确定每一步前提与结论间的关系，而且应遵循并运用有关推理规则。三、常用的有5个推理规则，即在证明的每一步上，都可以引入前提，所得结论都可引用为后继证明的前提，重言式中的任意命题变项都可用其他命题形式（处处）代入后仍得重言式，命题形式中的任何部分都可用与之等值的命题形式来置换（未必处处进行）其结果仍与原式等值；而分离规则为，若已知有A → B和A，则可推得B，若已知A → B和A为真，则得到的B也真。四、图式推理。乃省略证明所用定律的步骤，直接将前后件联系起来，则可得到推理定律与分离规则合而为一的图式推理，常用的有附加、化简、假言推理、拒取式、析取三段论等5种，每种都和一个推理定律相对应。五、有效证明与前提的一致性。每一步均由推理规则或图式得到，则证明与结论均有效，其仅与证明本身的构造方式有关而与前提的真假无关；当一个推理诸前提的合取式为可满足式时，则前提是一致的，其不会推出矛盾的结论；而诸前提的合取式为矛盾式时，则是不一致的，往往会推出矛盾的结论，但推理仍然是有效的。

所谓公理系统，乃只从给定的公理和规则出发，推导出一系列定理而形成的演绎系统。欧几里得的《几何原理》就是一个古典的公理系统；但由命题的重言式组成的现代公理系统，比古典系统更形式化、更严谨，但其公理的选择却是相对的，不像古典系统的公理一定比其他命题更为直观。命题逻辑有无限多重言式，有些反映了演绎推理的规则，欲无遗漏地包含于一个系统中以便从整体上加以考察，则必须借助公理系统。命题逻辑公理系统L，其定义：（一）字母表P ₁ ，P ₂ ，P _n ，…：¬，→；（二）合式公式①对每个i ≥ 1，Pi是合式公式；②如果A、B是合式公式，则（¬A），（A→B）也是；③合式公式仅由①或②形成。（三）公理（以公理模式形式给出，其中A，B，C表示任意合式公式）：（L1）（A→（B→A）；（L2）（A→（B→C））→（（A→B）→（A→C））；（L3）（（（¬A）→（¬B）→（B→A））。（为书写方便，最外层括号及（¬A）类型的括号均可省略）（四）推理规则：从A和（A→B）可以推得B，简称MP规则。L中的证明，是一个由合式公式A ₁ ，A ₂ ，…，A _n 组成的有穷非空序列，使对每个i（1 ≤ i ≤ n）Ai或是公理，或是序列前面的两个公式A _j ，Ak（j，k<i）应用MP规则直接推出的结论，则该序列称作A _n 在L中的证明，且A _n 为L的定理，记作上 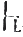A _n 。一般为缩短冗长的证明，L系统还引进一些类似推理规则的元定理，主要是演绎定理和可由之导出的称为“假言三段论规则”的HS规则，从而提供了定理证明的新途径。系统构成后，一般尚需对其推演能力，即对该系统的可靠性、一致性和完备性问题做出证明，从而考察：所推出的定理是否都是重言式？是否会推出矛盾的结果？以及，所有重言式是否都能从该系统推出？因在L系统的演算中，是以L的所有合式作真值指派的，故在L上的赋值可有无穷多种，而不是n个特定命题变项只有2 ⁿ 种真值指派，但其值域仍然是{0，1}，故在对“赋值”和“重言式”做出更严格定义的基础上，对L推理能力可做出证明，L是一个理想的命题逻辑的公理系统。

命题逻辑是以简单命题为基础即作为基本对象考察的，若对构成简单命题的个体词、谓词、量词诸成分作深层分析，而考察其命题形式与逻辑关系，则无能为力。对此，需要引进一阶逻辑（狭谓词逻辑），其亦具有自然推理和公理系统演算两种推理形式，其与命题逻辑共同构成整个现代逻辑的起点与基础，在诸多逻辑分支学科中有广泛应用，兹不赘述。

以上对命题逻辑要义之阐述，力求较全面系统又不失简明性，对尚未展开论述的诸多重要之点，作附列资料补充，以供研究参阅。

附列资料：

1.等值演算20律

（1）双重否定律p⇔¬（¬p）

（2）∨的幂等律p⇔（p∨p）

（3）∧的幂等律p⇔（∧p）

（4）∨的交换律（p∨q）⇔（q∨p）

（5）∧的交换律（p∧q）⇔（q∧p）

（6）∨的结合律［（p∨q）∨r］⇔［p∨（q∨r）］

（7）∧的结合律［（p∧q）∧r］⇔［p∧（q∧r）］

（8）∨对∧的分配律［p∨（q∧r）］⇔［（p∨q）∧（p∨r）］

（9）∧对∨的分配律［p∧（q∨r）］⇔∨（p∨r）］

（10）反演律¬（p∨q）⇔（¬p∧¬q）

（11）反演律¬（p∧q）⇔（¬p∨¬q）

（12）零律（p∨1）⇔1

（13）零律（p∧0）⇔0

（14）同一律（P∨0）⇔P

（15）同一律（P∧1）⇔P

（16）排中律（P∨¬P）⇔1

（17）矛盾律（P∧¬P）⇔0

（18）等价（p↔q）⇔（p→q）∧（q→p）

（19）蕴涵（p→q）⇔（¬P∨q）

（20）归谬（p→q）∨（→¬q）⇔¬p

以上各式中的p，q，r等变项，均可用任意的命题形式A，B，C分别代入，等值式仍然成立。

2.关于范式的几个概念和定理

（1）简单析（合）取式是仅由命题变项p，q，r，…或其否定¬p，¬q，¬r，…的析（合）取组成的合式公式

（2）定理 一个简单析取式是重言式当且仅当它至少同时含有一个命题变项P及其否定¬P；一个简单合取式是矛盾式当且仅当它至少同时含有一个命题变项P及其否定¬P

（3）析取范式 是简单合取式的析取；合取范式 是简单析取式的合取

（4）定理 任意给定的命题形式A，都有与之等值的析取范式和合取范式

（5）求命题形式A析（合）取范式的步骤：

①消去A中（若有）的联结词→，↔［以等值式（18）（19）可以实现］

②¬的内移或消去［可由等值式（1）将双重否定号消去，由反演律可将括号外¬号内移］

③应用分配律求得简单合取式的析取，或简单析取式的合取

（6）定理 一析取范式是矛盾式当且仅当它与其中的每个简单合取式是矛盾式；一合取范式是重言式当且仅当它其中的每个简单析取式是重言式

（7）几个命题变项的极小（大）项，是对每个Pi（q≤i≤n）以Pi或¬Pi的形式恰好出现一次，但两者不能同时出现，出现时固定在左起第I个位置上的简单合（析）取式；对于n个命题变项，可组成2n种不同的极小（大）项

（8）主析（合）取范式 是仅由极小（大）项组成的析（合）取范式

（9）定理 命题逻辑任意给定的命题形式A都有与之等值的主析（合）取范式

（10）求法步骤 先求出A的析（合）取范式，再按步进行：

①展开［用等值式A⇔→ A∧（pi∨¬pi）⇔（A∧pi）∨（A∧ ¬pi）或A⇔→A∨（pi∧¬pi）⇔（A∨pi）∧（A∨¬pi），把不含有某命题变项Pi的简单析（合）取式，置换成含有此项的式子］

②消去［把重复出现的简单合（析）取式、矛盾式（重言式）及简单合（析）取式中重复出现的命题变项消去］

③排序［把简单合（析）取式中的命题变项，按每一字典顺序p，q，r，…或p ₁ ，p ₂ ，p ₃ ，…统一排序；再按顺序排列式中的极小（大）项］。经有限步等值演算，总可得到与A等值的主析（合）取范式

（11）定理 命题逻辑中与任意给定的命题形式A等值的主析（合）取范式是唯一的

（12）由以上有关定理可知，两命题形式等值当且仅当它们对应的主析（合）取范式相同

3.常用的重言蕴涵式（9式）

另外，前20个等值可各自分解成的两个蕴涵式共40式。

（1）附加P⇒（p∨q）

（2）化简（p∧q）⇒p，q

（3）假言推理［（p→q）∧p］⇒q

（4）柜取式［（p→q）∧¬q］⇒¬p

（5）析取三段论［（p∨q）∧¬p］⇒q

（6）假言三段论［（p→q）∧（q→r）］⇒（p→r）

（7）等价三段论［（p↔q）∧（q↔r）］⇒（p↔r）

（8）构造性二难推理［（p→q）∧（r→s）∧（q∨r）］⇒（q∨s）

（9）破坏性二难推理［（p→q）∧（r→ s）∧（¬q∨¬s）］⇒（¬p∨¬r）

4.常用推理图式（5式）

（实际运用横线及“∴”号可省略）

（1）附加

（2）化简

（3）假言推理

（4）柜取式

（5）析取三段论

5.演绎定理和HS规则

定义 令Γ是L中的合式公式集（可能空）：L的一个有穷非空合式公式序列A1，…，An是Γ的一个推演，如果对每个i（1≤i≤n）有三者之一成立：

（1）Ai是L的公理

（2）Ai是Γ中的合式公式

（3）Ai是序列前面两个公式用MP规则直接推得；则合式公式An称作Γ在L中的一个结论，记作

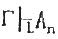
演绎定理 如果说Γ∪ {A} 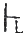B，则Γ 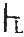（A → B）；其中，A，B为L的任意合式公式，Γ为L的合式公式集（可能空）。（可令B的推演长度为K，对K=1，K=n+1，按B是Γ定义中的三种情况或B是A等用L的定理及M规则作归纳证明）

HS规则{（A→B），（B→C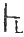）} （A→C）。（可由MP规则和演绎定理证得）

6.关于“赋值”的严格定义及L的推理能力（证明简述）

赋值定义 L的赋值函数V其定义域是L的合式公式集，值域是{0，1}；要求对L的合式公式A，B有：（1）V（A）≠ V（¬A）；（2）V（A→B）=0，当且仅当V（A）=1且V（B）=0（两条要求保证一个赋值不会自相矛盾）

重言式定义 对L的每个赋值V有V（A）=1：可满足式定义，存在V使V（A）=1；矛盾式 定义对所有V，V（A）=0

L的可靠性定理 L的每个定理都是重言式（可用归纳法，设长度K=1，则A为公理，定理成立；设1≤K≤n结论成立；再以赋值定义可反证得K=n+1时，A为重言式）

定义 L的扩充是由改变或扩大L的公理集，使L的定理仍保留为定理所得的公理系统；L的扩充是一致的，即如果没有L的合式公式A，A和（¬A）都是扩充的定理

L的一致性定理 L是一致的（可由可靠性定理及赋值定义反证）

定理 令L*是L的一致扩充，并且令A是L的合式公式但不是L*的定理。L**是由L*附加上（¬A）作为公理得到的L的扩充，则L**也是一致的（可以归谬法对所给条件反证）

定理 令L是L*的一致扩充，则存在着L*的一致的完全的扩充（可证一致的、完全的）

定理 如果L*是L的一致扩充，则存在着使得L*每个定理取值为1的赋值

L的完备性定理 如果A是L上的合式公式并且是重言式，则 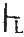A。（可据一致性的有关定理和赋值要求反证）（由该定理可知，A是L中的定理，当且仅当它是L的重言式，此正是理想的命题逻辑公理系统应具备的性质）

注释：

[1]马玉珂：《西方逻辑史》，北京：中国人民大学出版社1985年第1版。

[2]陈进元：《命题逻辑与一阶逻辑》，转引自《现代逻辑科学导引》上册，北京：中国人民大学出版社1987年第1版。

[3]周昌宗：《逻辑方法》，转引自《现代逻辑科学导引》下册，北京：中国人民大学出版社1987年第1版。 IHGLdrWeO+sq8VQiQ4v9lj03fwrh+x4PYY3+0YG24XfJQTTfQG4ThumvGdws57up