




在我与路易斯共事的那一年,一位名叫阿米塔巴·森(Amitaba Sen)的年轻博士后发表了两篇论文,让许多人感到兴奋和困惑。因为阿米塔巴·森正在尝试从超引力中创造一个量子理论,所以我们带着极大的兴趣阅读了他的两篇论文。论文中嵌入了几个引人注目的方程,其中爱因斯坦的引力理论被一套比爱因斯坦用过的更简单、更漂亮的方程表达了出来。我们几个人花了很多时间讨论,如果找到一种方法将量子引力建立在这些简单得多的方程上,将会怎样。但那会儿我们什么都没做。
唯一认真对待阿米塔巴·森的方程的人是阿布海·阿希提卡。他是经典相对论的支持者,在职业生涯早期,在这方面做过重要贡献,但后来他把研究重心偏向了量子引力理论。阿布海倾向于数学方法,他发现阿米塔巴·森的方程包含了爱因斯坦广义相对论重新表述的核心,在此基础上,一年后他真的建立了广义相对论的新表述。两个影响由此产生:它极大地简化了这个理论中的数学,并且用数学语言进行了表述,而这种数学语言与QCD中用过的语言非常接近。这正是将量子引力转化为一门真正的学科所需要的。在这门学科中,量子引力在时间上可以进行计算,从而在普朗克尺度上对空间和时间结构做出明确的预测。
在我刚刚成为耶鲁大学的助理教授时,我曾邀请阿布海在耶鲁大学做了一个演讲。那天来听演讲的学生中有一位来自哈佛的研究生,名叫保罗·伦特恩(Paul Renteln),他刚好也在研究阿米塔巴·森的论文。我们很清楚,阿布海的方程是进一步研究的关键。演讲之后,我载阿布海去哈特福德(Hartford)机场。在纽黑文(New Haven)和哈特福德之间一个小时的车程中,我的车有两个轮胎都漏气,不过阿布海仍然赶上了他的航班。但是最后一小段路,他不得不搭便车,而我则在路边等待救援。
那天一回到家,我就立刻坐了下来,开始应用阿米塔巴·森和阿布海的新形式体系,也就是我和路易斯在重新构建弦理论的失败尝试中发展出来的方法。几周后,在圣巴巴拉的理论物理研究所开始了为期一个学期的量子引力研讨会。我又非常幸运,就在耶鲁大学刚刚聘用我之后,我说服了学校领导让我在那里待上一个学期。我一到那里就找来了两个朋友,特德·雅各布森和保罗·伦特恩一起做事。我们很快就发现,如果用一些非常像电超导体的图景来表示引力场的通量线,就能描绘出一个非常简单的空间量子结构的图像。起初我和保罗一起工作,为了避免连续空间的无穷性,我们借鉴了威尔逊的格点。然后,我们发现爱因斯坦方程的新形式暗示了关于圈如何在格点上相互作用的非常简单的规则。但是我们遇到了和10年前一样的问题:如何消除由于使用一个固定格点而强加的背景。
特德·雅各布森建议我们试着跟随波利亚科夫的思路继续研究,并尝试在没有格点的情况下开展工作。我已经在第3章描述了这个结果。第二天,我们站在黑板前,盯着一个从来没有想过、也没有人想过要去寻找的东西,那就是量子引力理论完整方程的精确解。
我们所做的就是把建立量子理论的常用方法应用到阿米塔巴·森和阿希提卡发现的广义相对论方程的简单形式上去。这些方法引领我们提出了量子引力理论的方程式。这些方程最初是在20世纪60年代由布赖斯·德威特和约翰·惠勒写下的,但我们发现了一些更简单的新形式。我们必须代入这些方程来描述空间和时间几何的可能量子态。当时由于一时冲动,我尝试了路易斯和我一起研究出来的东西,也就是直接采用波利亚科夫表达式来建立这些态,描述电场的量子化圈。我们发现,只要圈不相交,它们就满足方程(如图10-1所示)。
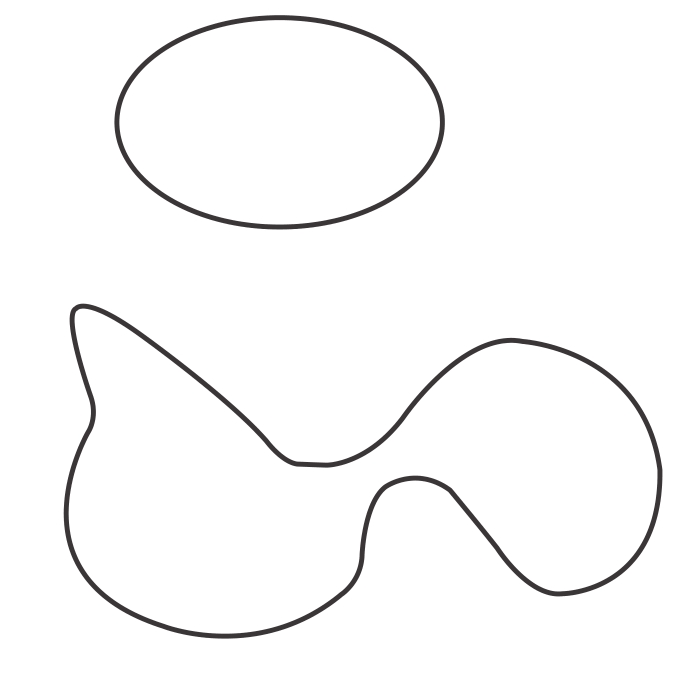
图10-1 空间几何的量子态
在圈量子引力理论中空间几何的量子态用圈来表示。只要圈之间没有交叉点或扭结,这些量子态就是量子引力方程的精确解。
我们花了几天的时间找到了更多的解。并且发现,即使圈相交,只要遵守某些简单的规则,我们仍然可以将它们结合起来,做出解。事实上,我们可以写出无穷多个这种态,并且所要做的就是画出圈,并在它们交叉的时候应用一些简单的规则。
我们和其他人花了很多年的时间才弄明白我们在那几天里所发现的东西的真正含义。但其实在一开始,我们就知道自己掌握了一个量子引力理论,这个理论开创性地给出了一个关于普朗克尺度物理学的精确描述,其中空间只不过由一组离散的基本对象之间的关系组成。这些对象仍然是威尔逊和波利亚科夫的圈,但它们不再存在于格点,甚至是空间里。相反,它们的相互关系定义了空间。
完成这个理论还差一步。我们必须证明我们的解是独立于背景空间的。这需要证明它们附加解决了微分同胚约束,并且表达了理论与背景的独立性。矛盾的是,我们很容易地解出了这些方程,即惠勒-德威特方程,而事实上,这些方程应该很难解才对。一开始我很乐观,但事实证明,要创造出能同时满足这两组方程的量子态是不可能的。解决一个问题很容易,但两全其美就比较难了。
第二年回到耶鲁大学,我们和路易斯·克兰一起花了很多时间来解决这个问题,但还是无果而终,因此我们确信这是不可能的。这件事令人非常沮丧,因为显而易见,如果想要摆脱背景依赖,就会得到一个只有圈和圈的拓扑关系的理论。圈在空间中的位置无关紧要,因为空间中的点没有内在的意义。重要的是圈如何相交,此外,它们如何打结和连接也很重要。
有一天,当我坐在圣巴巴拉的家的花园里时,我意识到了这一点。量子引力可以被简化为一种圈相交、打结和连接的理论。这样就可以得到一个普朗克尺度上的量子几何的描述。从我与保罗和特德的研究中,我也知道,我们所发现的爱因斯坦方程的量子版本可以改变圈相互连接和打结的方式,因此圈之间的关系可以动态变化。尽管我曾考虑过交叉的圈,但我从未想过圈是如何打结或连接的。
我进去给路易斯·克兰打了电话,问他数学家们是否知道圈如何打结和连接。他说,是的,有一个领域专门研究这个问题,叫作扭结理论。他还提醒我,我曾在芝加哥与扭结理论的一位重要思想家路易斯·考夫曼(Louis Kauffman)共进过几次晚餐。所以,最后一步是摆脱理论对圈在空间中的位置的依赖。这样,我们的理论就简化为对节点、连接和扭结的研究,美国主要的相对论学家之一詹姆斯·哈特尔(James Hartle)在不久之后就开始这样称呼它。但这并不容易,我们在一年多的时间里都没能迈出这一步。我们和路易斯,以及其他人一起努力,但还是没能做到。
在圣巴巴拉研讨会的最后一个会议上,我们首次提出了自己的新成果。在那里,我遇到了一位年轻的意大利科学家卡洛·罗韦利,他刚刚获得了博士学位。那时,我们没有聊很多,但不久之后,他就写信来询问是否可以来耶鲁大学参观我们的实验室。那年10月,他来到了路易斯的公寓,住进了其中一个房间。他到的第一天,我就告诉他,我们无事可做,因为我们的工作完全陷入了困境。这项工作看起来很有前景,但路易斯和我已经发现最后一步毫无希望。我对卡洛说,欢迎他留下来,但考虑到工作的前景惨淡,他可能更愿意回到意大利去。那段时间确实很尴尬。然后,我想找点事谈,就问他是否喜欢航海。他说自己是一个狂热的水手,所以我们放下了一整天的科学研究,直接去了港口。耶鲁大学帆船队在那里留有船只,我们登上其中一艘帆船。整个下午,我们都在船上谈论我们交过的女朋友们。
第二天我没有见到卡洛。第三天,他出现在我的办公室门口,说:“我找到了所有问题的答案。”他的想法是对这个理论再做一次重新表述,这样基本的变量就变成了圈。问题是到那时为止,几乎所有的理论不仅都依赖于圈,还依赖于圈周围的场。卡洛发现,正是由于对场的依赖,才使研究无法进行下去。他还找出了如何摆脱这种依赖的方法,就是他的导师、帝国理工学院的克里斯托弗·艾沙姆发现的一种方法。并且,卡洛已经发现,只要把这种方法应用到圈中,就能得到我们需要的东西。我们只用了一天的时间就给出了完整的描绘。最后,我们构建出了一个理论,一种纯粹的圈理论,波利亚科夫曾把它称为伟大的梦想,它用方程简单地描述了真实世界的一个方面,并且这些方程可以精确地解出来。当用它来构建爱因斯坦的引力理论的量子版本时,这个理论仅仅依赖圈之间的关系,即它们如何相交、连接和打结。在几天之内,我们就证明了所有的量子引力方程都可以构造无限多的解,就像有一种方法可以解决所有可能的打结方式。
几周后,我们去了锡拉丘兹大学(Syracuse University),阿希提卡和阿米塔巴·森就是在那里的研究中心有了新发现,卡洛举办了关于量子引力新理论的第一次研讨会。在去机场的路上,我们被一个开着豪华轿车的家伙追尾了。人没有受伤,我的旧道奇飞镖的后保险杠也几乎没有刮伤,但那个撞我们的家伙的玛莎拉蒂却被撞坏了。尽管如此,我们还是赶上了飞机。第二天卡洛发高烧,但他依然把研讨会挺了过去。研讨会的最后,是长时间的、感激的沉默。阿希提卡说这是他第一次看到可能是量子引力理论的东西。几周后的伦敦,在去印度参加会议的途中,我在克里斯托弗·艾沙姆面前举办了关于新理论的第二次研讨会。
在印度,当我把会议组织者介绍给卡洛时,两种古老的文化相遇了。卡洛冲动地跳上飞机就来了,事实上他并没有收到邀请。那位尊贵的绅士看了看他的长发、凉鞋和衣服(这是他一个人在孟买的后街闲逛了两天淘到的),气急败坏地嚷道:“卡洛先生,你没有收到我的信说会议结束了吗?”卡洛微笑着回答说:“没有,但你没有收到我的吗?”然后他被安排住在酒店里最好的房间,返回罗马时,被安排坐在印度航空航班上的头等舱。
这便是圈量子引力理论的诞生。我们花了好几年的时间,先是与卡洛合作,后来加入了一个由朋友和同事组成的不断壮大的群体,阐明了我们发现的量子引力方程的解的意义。一个明确的研究结果是,我们发现量子几何是离散的。我们所做的一切研究都是以离散的力线为基础的,就像在超导体的磁场中一样。如果把它转换成引力场的圈图,这就意味着任何表面的面积都是以基础单位的离散倍数表示的。最小的单位是普朗克面积,即普朗克长度的平方。这意味着所有的表面都是离散的,每个表面都有有限的面积,体积也是如此。
为了得到这些结果,我们必须找到一种方法来消除困扰场的量子理论的所有表达式的无穷性。我的直觉源自过去与朱利安·巴伯的谈话,以及与路易斯·克兰的合作,我认为这个理论不应该有无穷性。许多物理学家也推测无穷性是基于普朗克尺度的关于空间和时间结构的一些错误假设。从较早的研究工作中,我清楚地看到错误的假设是指假定时空的几何结构是固定的、非动态的。在计算几何尺寸(如面积和体积)时,我们必须用正确的方式消除固定结构的任何可能的影响。做到这一点的方式太过技术性,在这里无法解释。但最终事实证明,只要提出的是一个有意义的问题,就不会有无穷性。
根据我的经验,一位科学家只会有几个好想法。好的想法很少而且会间隔很久,需要经过多年的准备。更糟糕的是,一旦有了好想法,就注定要经过多年的艰苦努力去研究它。当我在一个汽车修理厂的嘈杂房间里坐了一个小时,等着我的车修好的时候,我试图计算一些量子几何的体积,并突然想到面积和体积可能是离散的。我的笔记本上满是杂乱的积分,但突然间我看到了一个计算公式。我在假设结果是实数的基础上开始计算一个量,但发现在某些单位中,所有可能的答案都是整数。这意味着面积和体积不能取任何值,而是以固定单位的倍数出现。这些单位对应着最小的面积和体积。我把这些计算结果拿给卡洛看,几个月后,我们在意大利东北部山区的特伦托大学一起工作时,卡洛提出了一个论点,即面积的基本单位不能近似为零。这就意味着如果我们的理论是正确的,则无法避免这样的结论:空间有一个原子结构。
我之所以清楚地记得我们在特伦托的工作,还有另一个原因。前一年,一个名为贝恩德·布鲁格曼(Bernd Bruegmann)的学生带着非常不安的表情来到我的办公室。他的论文的主题是把量子引力的新方法应用到格点上的QCD,看看质子和中子的性质是否会出现。在这样做的同时,他还做了优秀科学家应该做而我们没有做的事情,那就是彻底查阅文献。然后,他发现了一篇方法与我们非常相似的论文,已经被我们从未听说过的两个人——鲁道夫·甘比尼(Rodolf Gambini)和安东尼·特里亚斯(Anthony Trias),应用于QCD,他们在蒙得维的亚(Montevideo)和巴塞罗那(Barcelona)工作。
科学家也是人,我们都需要觉得自己的工作很重要。对科学家来说,几乎最糟糕的事情莫过于发现有人在你之前就有跟你同样的发现。唯一更糟糕的是,有人发表了你在此前已经发表了的发现,却没有给你足够的承认。我们发现的方法的确是用来处理圈量子引力领域而不是QCD领域的问题的,但是我们也无法回避,其很接近鲁道夫·甘比尼和安东尼·特里亚斯应用于QCD的方法,并且他们的应用早于我们很多年。尽管他们已经在主要期刊《物理评论》( Physical Review )上发表了文章,但不知何故,我们并未看到。
我们怀着沉重的心情做了唯一能做的事,那就是坐下来给他们写一封道歉信。直到有一天下午在特伦托,卡洛接到一个巴塞罗那打来的电话时,我们才听到他们的消息。他们终于收到了我们的信。他们知道我们在特伦托,问我们明天是否还在。晚上,他们驾车穿越了意大利北部和法国,找到了我们。我们一起度过了美好的一天,向彼此展示各自的工作,谢天谢地,我们的研究是互补的。他们把这个方法应用于QCD,而我们把它应用于量子引力。安东尼·特里亚斯说了很多话,而鲁道夫·甘比尼则坐在房间后面,一开始几乎什么也没说。但我们很快发现,鲁道夫是一流的创造性科学家。在接下来的几个月里,他迅速发明了一种新的方法,可以在圈量子引力理论中进行计算。
此后,鲁道夫一直是量子引力领域的领军人物之一,经常与宾夕法尼亚州立大学的乔治·普林(Jorge Pullin)以及他自己在蒙得维的亚培养的一个优秀的年轻团队一起工作,他们发现了更多量子引力方程的解,并解决了一些重要的问题。
必须指出的是,尽管鲁道夫·甘比尼性情安静,但在国家被军事独裁彻底摧毁后,他或多或少地独自肩负着委内瑞拉和乌拉圭的物理学的复兴重任。当我第一次访问蒙得维的亚时,我意识到了这意味着什么。那是隆冬时节,我们和鲁道夫·甘比尼以及他的小组在一个破旧的修道院里做物理研究,没有暖气,也没有电脑,我们只能靠不断地喝在煤气灯上烧着的茶来取暖。现在,乌拉圭大学的科学系都建在现代化的建筑和设施中,这些建筑和设施都是用鲁道夫在业余时间筹集的资金建造的,同时他不断地有新的想法,进行新的计算。
圈量子引力理论带来的最美丽的结果之一是发现圈的态可以出现在非常美丽的图景中,即自旋网络。自旋网络实际上是30年前由罗杰·彭罗斯(Roger Penrose)发明的。彭罗斯也受到空间必须是纯粹关系的观点的启发。但他能够直接进入问题的核心,而不是像我们一样试图从一些现有的理论中推导出关系空间图。他更有勇气,寻求可能是量子几何理论基础的最简单的关系结构。他想出的便是自旋网络。自旋网络只是一个图(如图10-2、10-3、10-4和10-5所示),其边缘由整数标记。这些整数来自量子理论中粒子的角动量允许的值,它等于一个整数乘以普朗克常数的一半。
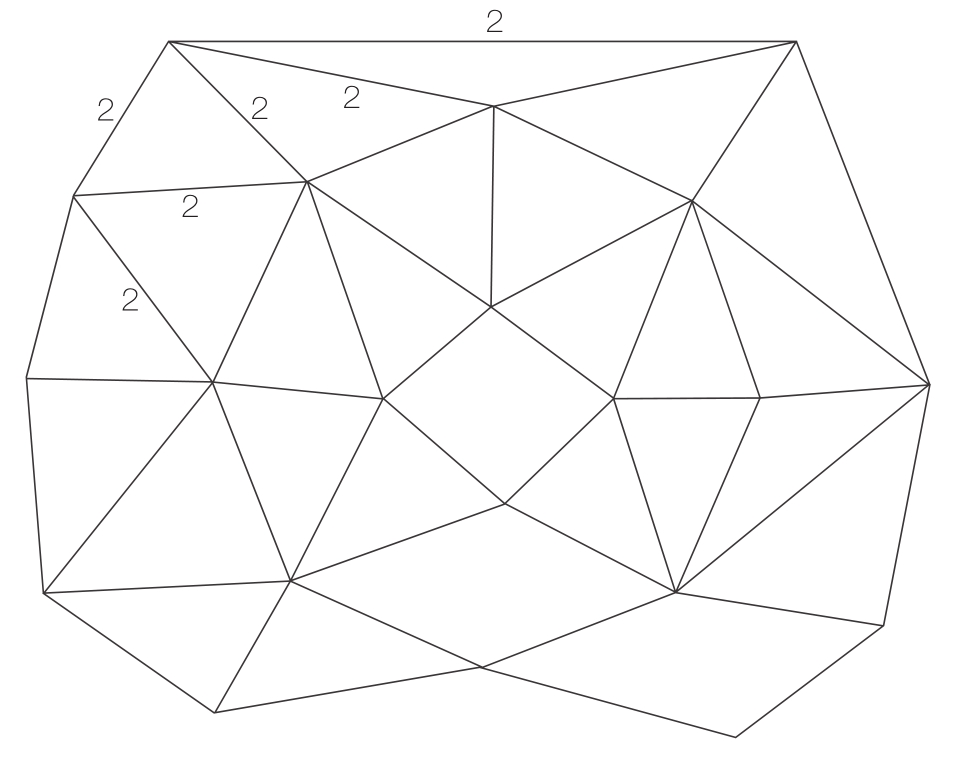
图10-2 自旋网络示意图
由罗杰·彭罗斯发明的自旋网络也代表了空间几何的量子状态。它由一个图形和边线上的整数组成。这里只显示了少部分数字。
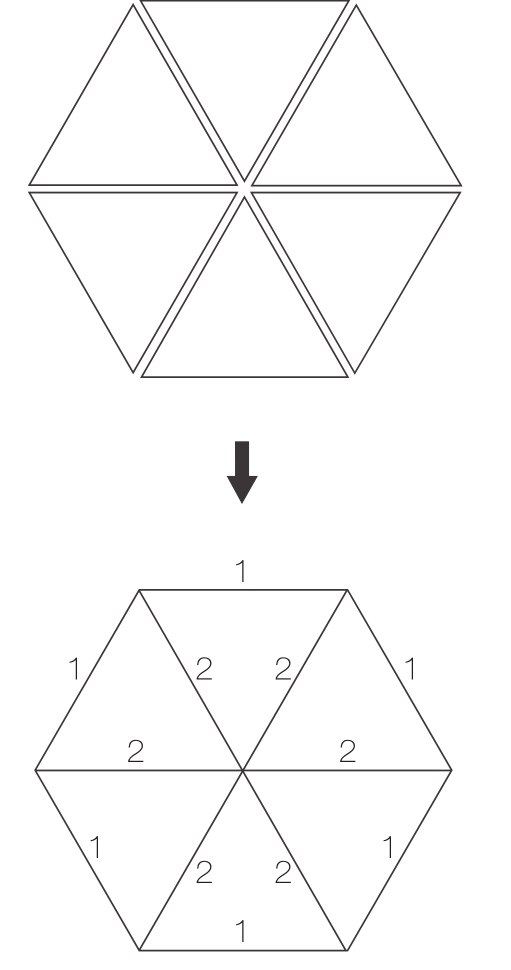
图10-3 对圈进行组合而形成的自旋网络
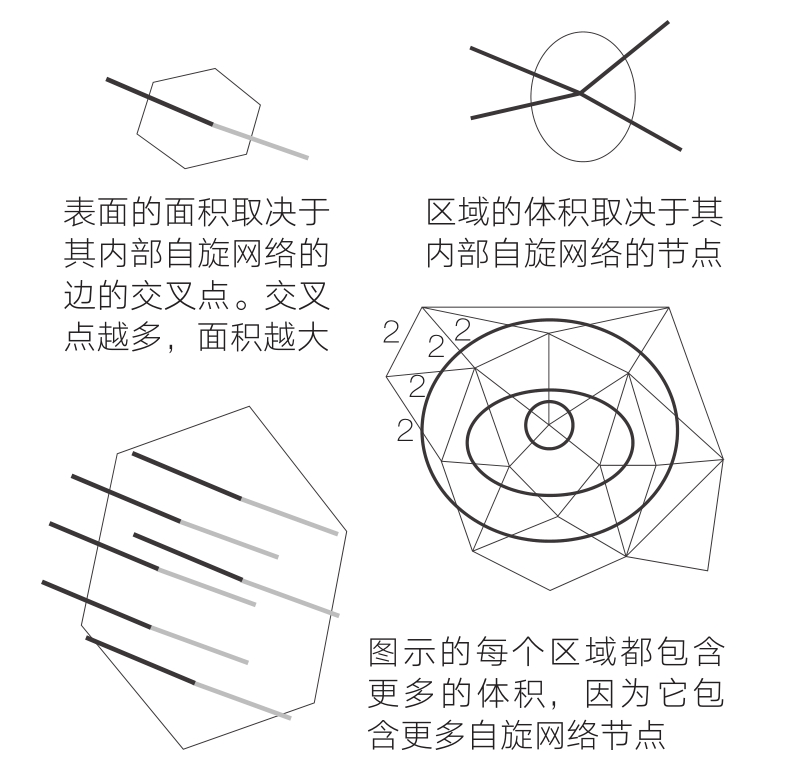
图10-4 有多个节点的自旋网络
圈量子引力理论预测的空间的量子化。自旋网络的边缘携带着离散的面积单位。表面的面积来自其自旋网络的边的交叉点。最小的面积来自一个交叉点,大约是10 -66 平方厘米。自旋网络的节点携带离散的体积单位。最小的体积来自一个节点,大约是10 -99 立方厘米。
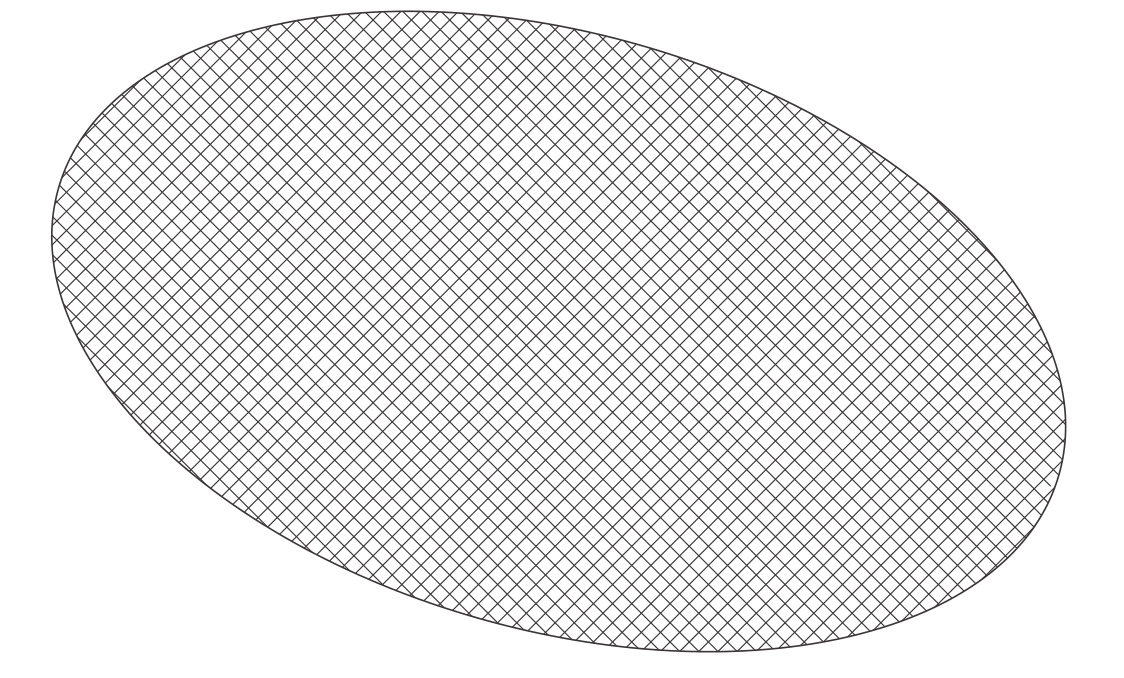
图10-5 代表量子几何的大规模自旋网络
一个非常大的自旋网络可以代表一个量子几何,它从比普朗克长度大得多的尺度上看起来是平滑和连续的。因此我们说经典的空间几何是由一个非常大且复杂的自旋网络编织而成的。在自旋网络图中,空间只不过看起来是连续的,但实际上是由构成自旋网络的节点和边缘组成的。
我早就知道彭罗斯的自旋网络应该纳入圈量子引力理论,但我一直避免工作中掺杂自旋网络。当彭罗斯在他的演讲中描述自旋网络时,它们总是看起来很复杂,仿佛只有彭罗斯才能在自旋网络中进行计算而不出错。要用彭罗斯的方法计算,你必须把一长串数字加起来,每一个都是+1、0或-1。如果你忽视了一个符号,你就死定了。不过,在1994年访问剑桥大学期间,我遇到了彭罗斯,并向他请教如何计算他的自旋网络。我们有幸一起做了一个计算,并且我认为自己也掌握了窍门。这足以让我相信自旋网络可以计算出量子几何的各个方面,比如最小的体积。然后我向卡洛展示了我所学到的东西,我们用那个夏天剩下的时间把我们的理论翻译成了彭罗斯的自旋网络的语言。
在做这项工作的时候,我们发现每个自旋网络都为空间几何提供了一个可能的量子态。其中,自旋网络每条边上的整数都对应于这条边所承载的面积单位。并且,自旋网络的线承载的是面积单位,而非一定数量的电或者磁通量。自旋网络的节点也有一个简单的含义,即对应量化的体积单位。如果用普朗克单位来衡量,一个简单自旋网络中包含的体积基本上等于网络的节点数。为了弄清楚这幅图,我们花费了很多心血。彭罗斯的方法是无价的,但正如我所预料的那样,使用起来并不容易。在此过程中,我们对理查德·费曼曾经说过的一句话深有感触:一位优秀的科学家会努力工作,并且不惜犯任何可能的错误来找到正确的答案。
我在科学领域最糟糕的时刻可能是在华沙的一次会议上,有一位名叫雷娜塔·罗尔(Renate Roll)的年轻物理学家上台发言,她在伦敦的时候也曾是克里斯托弗·艾沙姆的学生,她在发言的最后指出我们在最小体积方面的计算是错误的。经过一番争论,事实证明她是对的,后来我们发现计算的错误最终来源于一个符号的错误。但幸运的是,我们的基本框架和结果都是站得住脚的,并得到了数学物理学家的证实,他们用严格的数学定理支持了我们所发现的结果。数学物理学家的工作表明,量子几何的自旋网络图不只是一些人想象的产物,而是直接结合量子理论和相对论的基本原理而来。
圈量子引力的方法现在是一个蓬勃发展的研究领域。许多较早的想法也已经被纳入其中,如超引力和量子黑洞的研究。人们发现了量子引力的其他方法之间的联系,比如阿兰·孔涅的非交换几何方法、罗杰·彭罗斯的扭量理论和弦理论。
我们从这次经历中体会到,当具有不同教育背景的人们跨越国界联合起来的时候,科学进步的速度会有多快。理论物理学家和数学物理学家之间的关系并不总是融洽的。这就像第一次探索边疆的侦察兵和紧随其后的农民之间的关系,前者用篱笆把土地围起来,而后者则使土地肥沃起来。数学家们就像农民一样,需要把所有东西都固定下来,并确定一个想法或结果的确切界限,而物理学家就像侦察兵,其想法往往有些疯狂和野性。每个人都倾向于认为自己做了工作的重要部分。不过,我们和弦理论学家都知道的一点是,尽管他们的工作和思维方式不同,但数学家和物理学家学会相互交流和合作是很重要的。与广义相对论的境遇相同,量子引力既需要新的数学知识,也需要新的概念、思想和计算方法。如果我们取得了真正的进展,那是因为人们的共同努力可以创造出任何人都不可能独自想出的东西。
最后,圈量子引力给出的空间绘景最令人满意的地方是其完全相关性。自旋网络并不存在于空间中,相反,是它们的结构生成空间。实际上,自旋网络只不过是一种关系结构,该结构由节点上的边缘如何联系在一起决定。同样被编码的还有关于这些边如何扭结和连接的规则。同样令人满意的是,经典几何和量子几何之间有着完全的对应关系。在经典几何中,区域的体积和表面的面积取决于引力场的值。它们被编码在一些复杂的数学函数集合中,统称为度规张量(metric tensor)。而在量子几何中,几何图形由自旋网络的选择编码而成。这些自旋网络与经典描述相对应,在任何经典几何中,你都可以找到一个自旋网络描述相同的几何(如图10-5所示)。
在经典的广义相对论中,空间的几何形状随时间而演化。例如,当引力波经过一个表面时,这个表面的面积会随时间而振荡。实际上这里也有一种等效的量子图,其中自旋网络的结构可能随着引力波的通过而随时间演化。图10-6显示了自旋网络随时间演化的一些简单步骤。
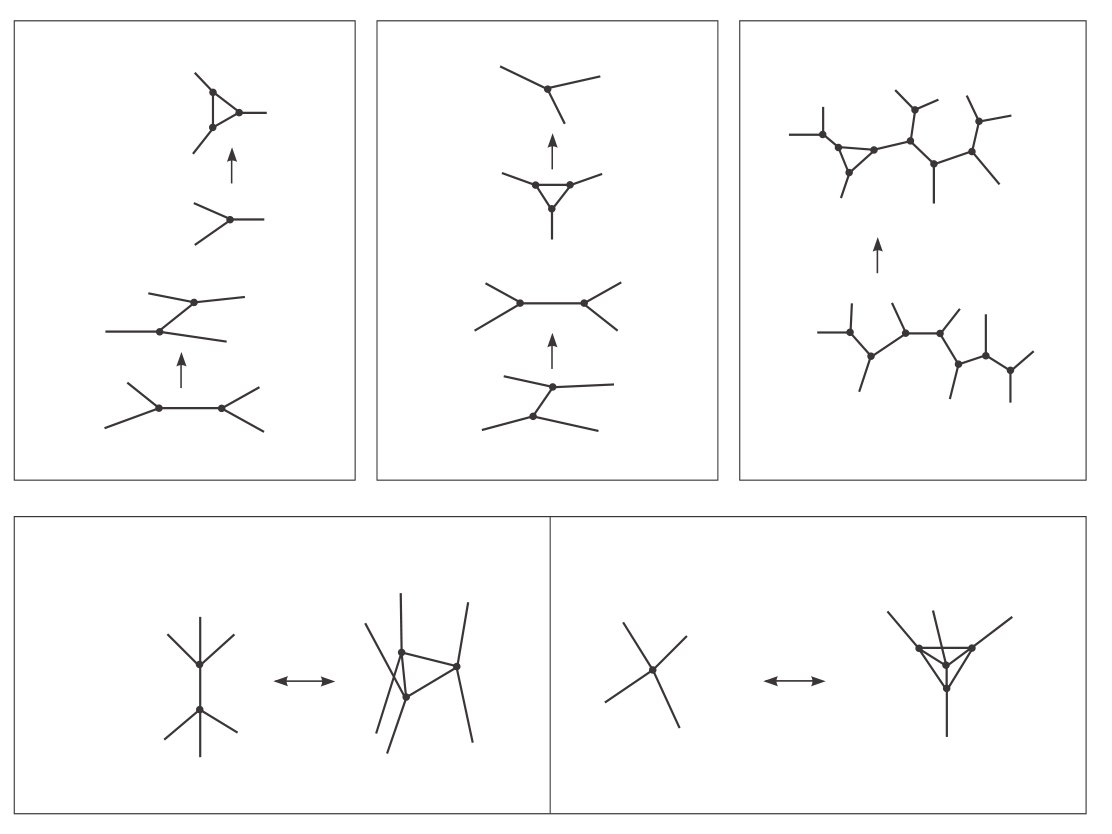
图10-6 一个自旋网络随时间演化的简单步骤
每一个都是空间几何的量子跃迁,这是爱因斯坦方程的量子理论类比。
如果让一个自旋网络演化,我们就会得到一个离散的时空结构。这个离散时空的事件是图10-6中所示形式发生变化的过程。实际上我们可以画出演化的自旋网络图,它们看起来就像图10-7到10-9。一个演化的自旋网络很像一个时空,但它是离散的而不是连续的。
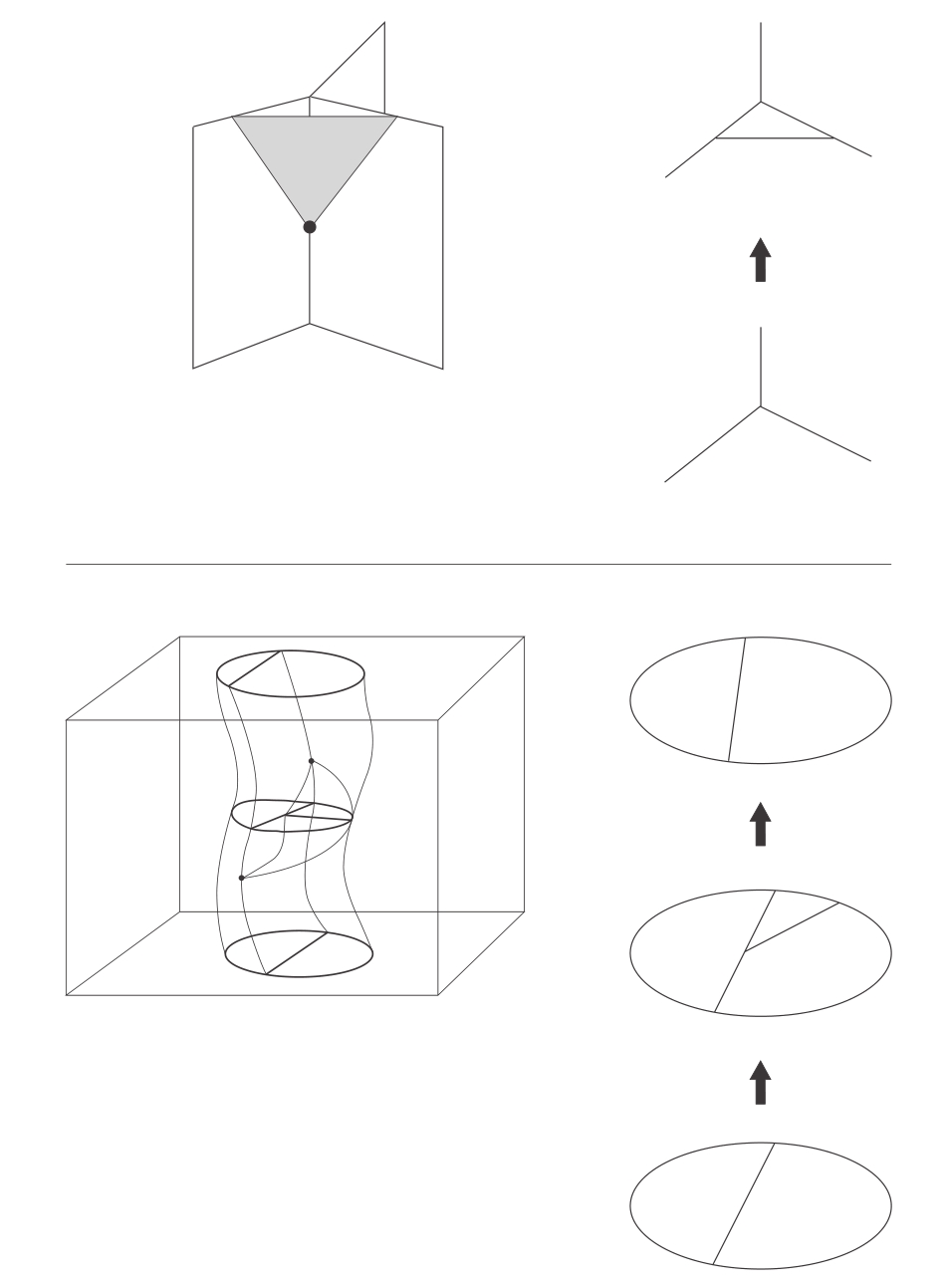
图10-7 两张量子空间的照片
量子时空中的每一个事件都是空间量子几何中的一个简单变化,对应图10-6所示的一个移动。根据圈量子引力理论,如果我们以10 -43 秒的时间尺度和10 -33 厘米的长度尺度来考察,这就是时空的样子。上图显示了一个基本的移动。下图显示了两个基本运动的合运动。
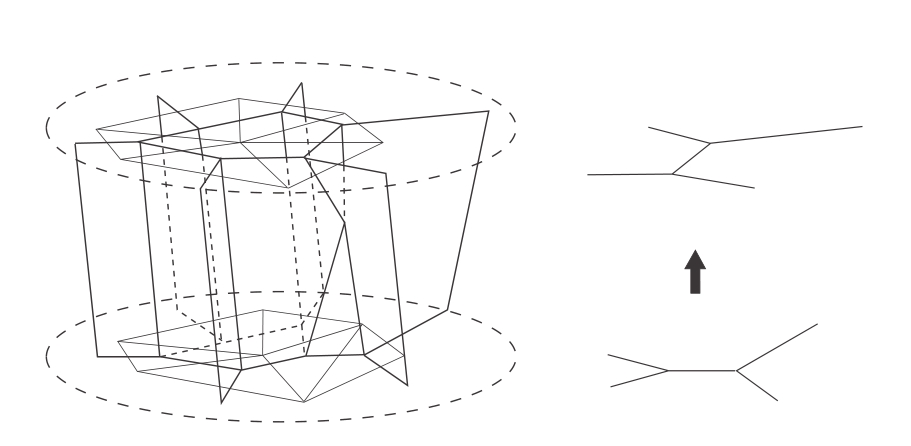
图10-8 量子跃迁
这是自旋网络中量子跃迁的另一个基本步骤,以及它的时空绘景。
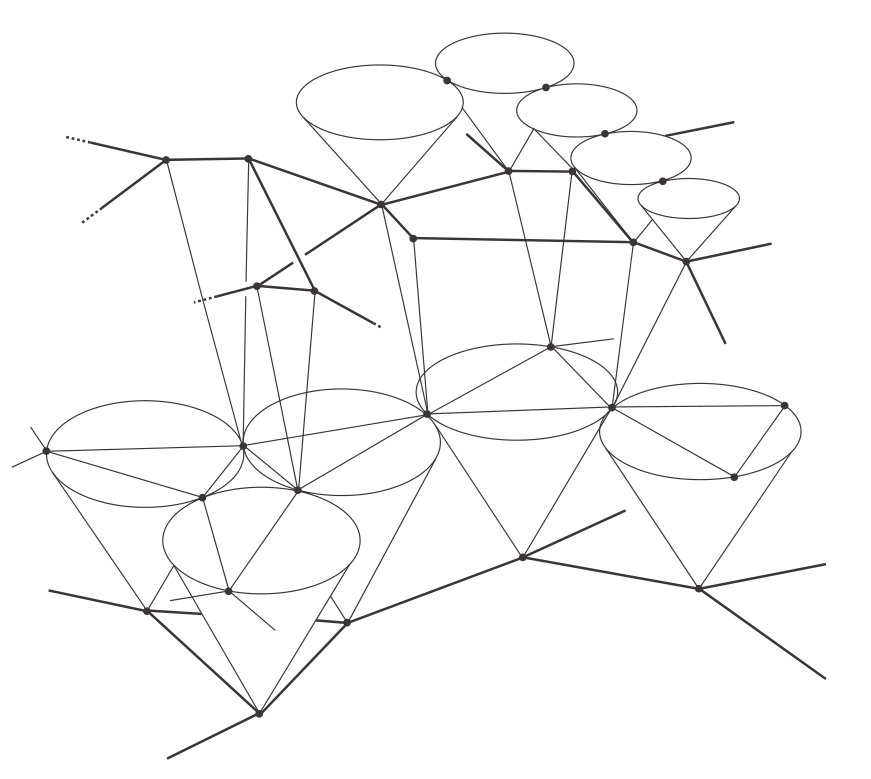
图10-9 自旋网络改变的事件的因果未来
另一张量子时空的图片,展示了自旋网络改变的事件的因果未来,用第4章介绍的光锥绘制。
我们能知道事件之间的因果关系是什么,所以自旋网络有光锥。但自旋网络还有更多的特性,因为我们可以通过自旋网络画出对应于时间矩的切片。
就像相对论一样,有许多不同的方法来切割一个演化的自旋网络,以便将其看作随着时间演化的一系列态。因此,圈量子引力理论给出的时空绘景与相对论的基本原理一致,即空间没有事物,只有过程。
约翰·惠勒曾说过,在普朗克尺度上,时空不再是平滑的,而是类似于泡沫,也就是他所说的时空泡沫。在向惠勒致敬时,数学家约翰·贝兹(John Baez)建议将演化中的自旋网络称为自旋泡沫(spin foam)。自20世纪90年代中期以来,有关自旋泡沫的研究如雨后春笋般涌现。目前有几个不同的版本正在研究中,分别是迈克·赖森伯格(Mike Reisenberger)、路易斯·克兰和约翰·巴雷特(John Barrett),以及福蒂尼·马可波罗-卡拉马拉这几位科学家的研究成果。卡洛·罗韦利、约翰·贝兹、雷娜塔·罗尔和许多其他对圈量子引力做出贡献的人现在都在从事自旋泡沫的研究。所以这是目前非常活跃的一个研究领域。图10-10展示了一个以自旋泡沫理论为基础的,只有一个空间和一个时间维度的世界的计算机模拟。这是简·安布杨(Jan Ambjorn)、科斯塔斯·阿纳格诺斯托普洛斯(Kostas Anagnostopoulos)和雷娜塔·罗尔的作品。这些宇宙非常小,每条边对应一个普朗克长度。但它们并不总是平滑演化,相反,宇宙的大小不时地突然跳跃,这就是几何的量子涨落。多年后,我们才得到一个真正的时空几何量子理论。
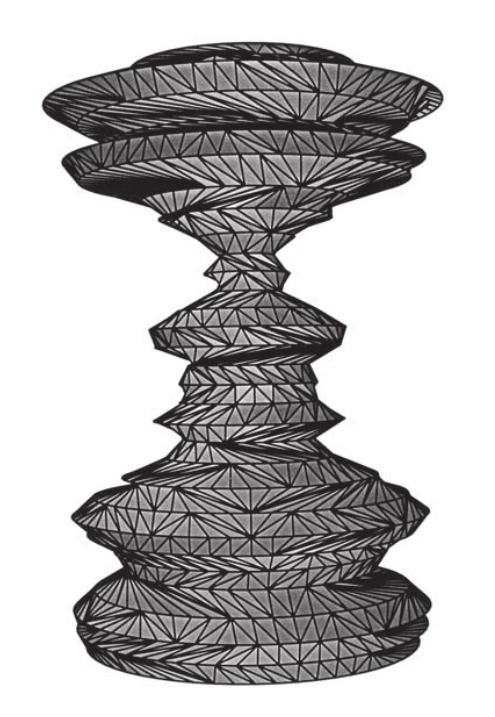
图10-10 量子时空的计算机模型
模型展示了一个只有一个空间和一个时间维度的宇宙。所示的结构存在于10 -33 厘米和10 -43 秒的尺度上。我们看到,由于不确定性原理,量子几何涨落非常剧烈。与原子中电子的位置一样,对于这么小的宇宙,宇宙大小的量子涨落非常重要,因为这些量子和宇宙本身一样大。
这个理论是正确的吗?目前,我们还不知道。不过,旨在测试该理论对面积和体积的离散性以及对时空几何的其他度量所做出的预测的实验终将会验证它。但我想强调的是,尽管它直接遵循了广义相对论和量子理论的结合,圈量子引力并不需要是一个完整的论述才是正确的。特别是该理论的主要预测,如面积和体积的量子化,其正确与否并不取决于许多细节的正确性,而是基于量子理论和相对论中最一般的假设。这些预测并没有限制世界上还有什么,有多少维度,或者基本对称是什么。而且,这些预测完全符合弦理论的基本特征,包括额外维度和超对称的存在。我没有理由怀疑它们的真实性。
当然,最终还是要靠实验来验证。但我们真的能指望在普朗克尺度上对空间结构进行实验验证吗?普朗克尺度可是比质子还要小20个数量级。直到不久之前,大多数人仍然怀疑能否在有生之年看到这样的实验。但现在我们知道自己太悲观了。富有想象力的年轻意大利物理学家吉乔瓦尼·阿米力诺-卡米利亚(Giovanni Amelino-Camelia)指出,他有一种方法可以检验“在普朗克尺度上空间几何是离散的”这一预测。在他的方法中,整个宇宙被他当作了一个工具。
当一个光子穿过一个离散的空间时,它会受到一些经典物理所预测的影响而偏离路径。这些偏差是由光子的相关波在被量子几何的离散节点散射时产生的干涉效应引起的。对于我们能探测到的光子,这些效应非常非常小。然而,在阿米力诺-卡米利亚之前,没有人想到光子在长距离传输时这些效应会累积,并且我们能够探测到穿过可观测宇宙大部分区域的光子。因此,他提出通过仔细研究卫星拍摄的非常剧烈的事件的图像,有可能用实验方法发现空间的离散结构,例如那些产生 x 射线和γ射线爆发的事件。
如果这些实验确实证明了空间在普朗克尺度上具有原子结构,那么这必将成为21世纪早期最令人兴奋的科学发现之一。通过研究这些新方法,我们可以看到空间离散结构的图像,就像我们现在能够研究原子阵列的图像一样。如果我在前两章中描述的工作是相关的,那么,我们将看到威尔逊和波利亚科夫的圈有序排列成彭罗斯的自旋网络。