加减法互相还原,乘除法也互相还原,这就是还原算的靠山。
“因为三加五得八,所以八减去五剩三,而八减去三剩五。又因为三乘五得十五,所以三除十五得五,五除十五得三。这是小学生都已知道的了。说得神气活现些,那便是, 加减法互相还原,乘除法也互相还原,这就是还原算的靠山。 ”马先生这样提出要点来以后,就写出了下面的例题。
例一: 某数除以2,得到的商减去5,再3倍,加上8,得20,求某数。
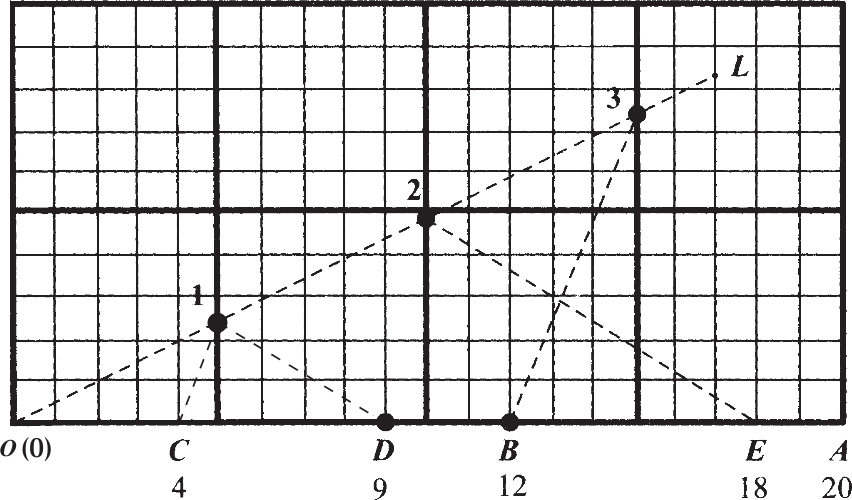
图60
马先生说:“这只要一条线就够了,至于画法,正和算法一样,不过是‘倒行逆施’。”
自然,我们已能够想出来了。
(1)取 OA 表20。
(2)从 A 点“反”向截去8得 B 点。
(3)过 O 点任画一直线 OL 。从0起,在上面连续取相等的三段得01,12,23。
(4)连3 B ,作1 C 平行于3 B 。
(5)从 C 点起“顺”向加上5得 OD 。
(6)连1 D ,作2 E 平行于1 D ,得 E 点,它指示的是18。
这情形和计算时完全相同。
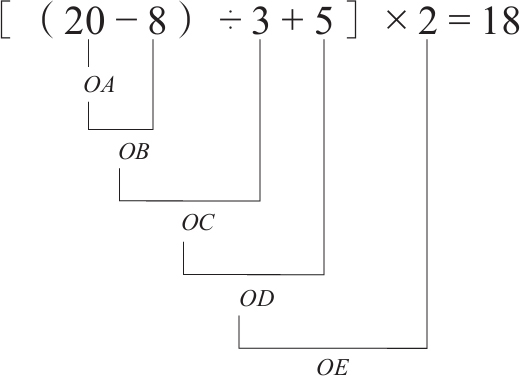
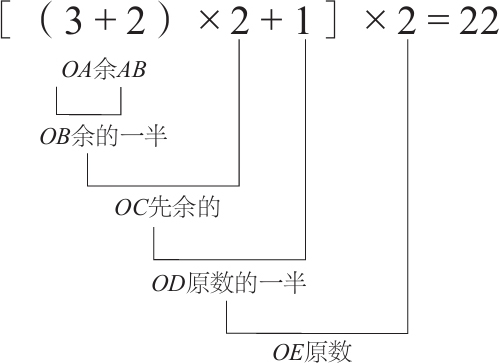
例二: 某人有桃若干个,拿出一半多1个给甲,又拿出剩余的一半多2个给乙,还剩3个,求原有桃数。
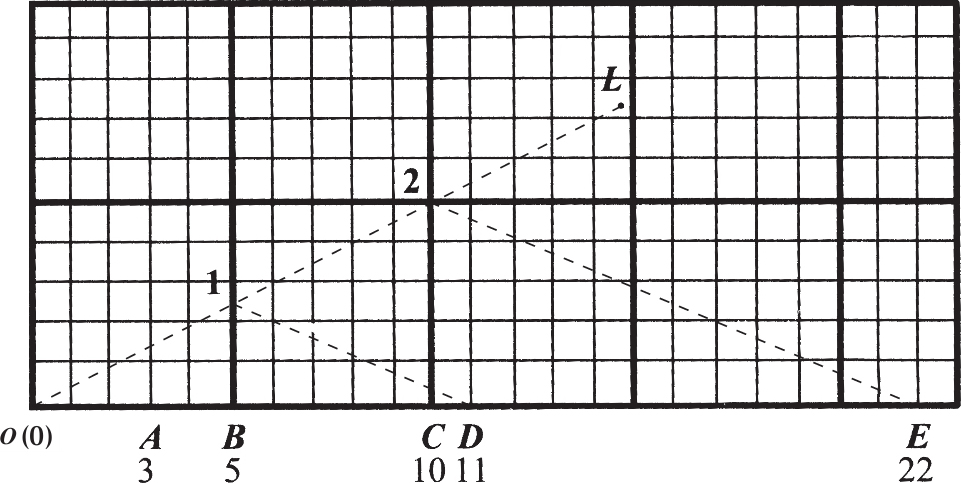
图61
这和前题本质上没有区别,所以只将图和算法相对应地写出来!