




威廉·配第导师一席话,让台下的学生有些摸不着头脑。“利息”这个概念大家都知道了,那“复利”又是什么呢?竟然能让诺贝尔奖的奖金永远都发不完?
王一也苦思冥想了良久,明明记得专业课导师提过的,怎么就是没印象呢?
威廉·配第导师似乎很满意大家这种困惑的表情,接着说道:“诺贝尔在全世界20个国家开办了约100家工厂,在弥留之际,诺贝尔立下了遗嘱,将自己的财产变作基金,每年用这个基金的利息作为奖金,奖励那些在前一年度为人类做出卓越贡献的人。大家记住,诺贝尔奖本金是3100万瑞典克朗。”
接着,他转身在黑板上写下这样一串数字:
1901年,奖金15万瑞典克朗;
1980年,奖金100万瑞典克朗;
1991年,奖金600万瑞典克朗;
1992年,奖金650万瑞典克朗;
2000年,奖金900万瑞典克朗;
2001年,奖金1000万瑞典克朗;
……
王一和大家一样,眼睛随着威廉·配第导师写下的数字越瞪越圆,不少学生都计算出,诺贝尔奖金发放的总额,早已远远超过诺贝尔遗产的本金数额。
威廉·配第导师笑着说:“如果没有复利,诺贝尔奖早已不复存在了。1953年,诺贝尔奖的资产只剩下300多万美元。加上通货膨胀的影响,这些钱只相当于1901年的30万美元。”
大家明知道诺贝尔奖并没有破产,但心还是不由自主地揪了起来,十分专注地看着威廉·配第导师。威廉·配第吊足了大家的胃口,满意地接着说:
“诺贝尔基金会的理事们求教于经济专家,用一种新的资产管理方式,一举挽回了诺贝尔奖的破产危机。不仅如此,到2000年之后,诺贝尔奖的总资产已经增长到超过5亿美元了。”
这时,王一听见有同学说:“我知道了!您是想说经济学上的‘72法则’!”威廉·配第导师向那位学生投去赞许的目光,然后向其他学生解释道:
“‘72法则’,就是用72除以回报率,可以估算出本金增减所需的时间,反映出复利的结果。举个例子吧,假如你将投入100万元,年利率是10%,那么,你的100万元增长到200万元,大约需要72÷10,也就是7.2年时间。”
威廉·配第导师一边说,一边把复利计算公式写到了黑板上: F = P (1+ i ) n 。
“其中, P 就是我们的本金,也就是那100万元;而 i 则是利率,也就是10%; n 为持有期限。”威廉·配第狡黠地眨了眨眼睛,“诺贝尔的财富真的很令人羡慕啊,而这也是利滚利最好的例证。”(如图1-3所示)
说到这儿,威廉·配第导师喝了口茶,满意地看着台下学生们瞠目结舌的样子。王一将威廉·配第导师的话好好消化了一番,才发现原来经济学这么有趣,难怪有这么多人都为经济学着迷。
威廉·配第导师补充道:“复利最大的魅力就在于,它不仅是本金产生利息,利息也能产生利息,就像滚雪球一样,越滚越大。”
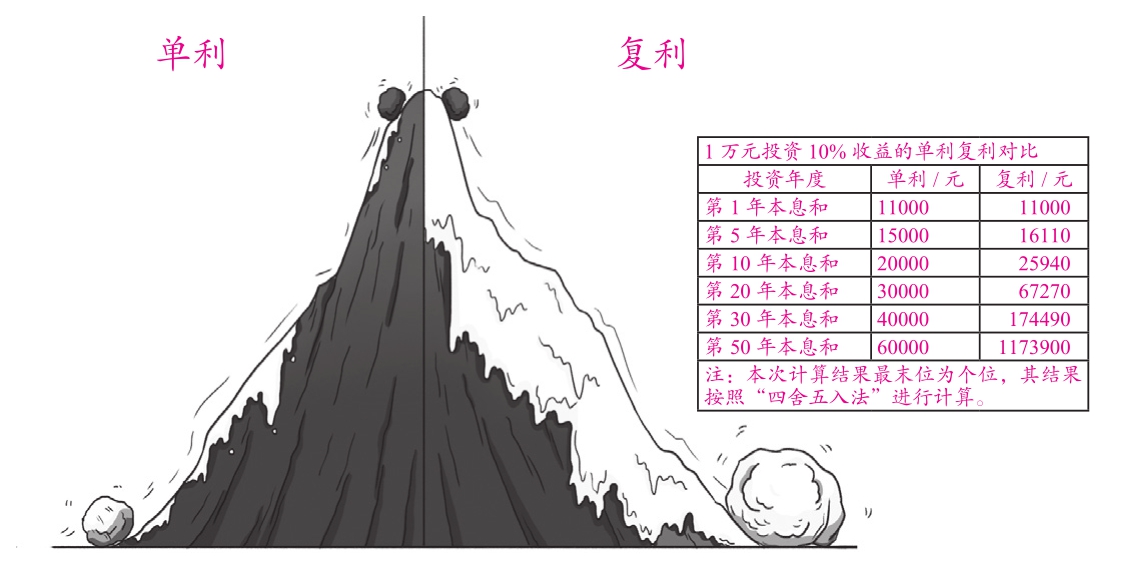
图1-3 单利与复利对比
威廉·配第导师耸耸肩,轻松地说:“躺着也能挣钱,这是一件真事。其实你也有希望登上富豪榜。也许你们当中有人会问:我怎么不知道还有这种好事呢?因为,你不懂复利。”
很多人包括王一,大家都认为致富的先决条件是庞大的本金,其实并非如此。“不积跬步,无以至千里;不积小流,无以成江海”就是这个道理。说白了,只要懂得复利,一粒米也能变成大粮仓。
威廉·配第导师让大家思考了一下自己的话,然后说:“我出一个问题,考考大家是否真的听懂了复利这个概念:有两个人,第一个在23岁的时候,每年投资1万元,直到自己45岁,按照年复利率15%的收益增长;另一位在32岁才开始投资,他每年投资2万元,同样是15%的复利率。当二人都到45岁时,谁的钱更多?”
王一听到有些学生小声说“投资两万元的更多”,也有人说“先投资的人钱更多”,但更多的学生则是拿出笔和本,仔细地计算着二人的所得。
最后,大家纷纷给出了答案:先投资的人赚得更多。
威廉·配第导师满意地笑了:“很好,看来你们都认真听讲了。先投资的人,在他45岁时,通过复利能得到约138万元,而后投资的人,到他45岁时只能获得68.7万元。这就是复利的时间力量。”
这个问题让王一想到了自己的姐姐,她也是早早就搞投资赚利息,拿了家里的100万元做抵押理财,年利率是10%,一年后,对方付给他姐姐110万元。然后,他姐姐又拿110万元继续做理财,依旧是10%的年利率。
第二年,这110万元的利息变成了11万元,本息加起来是121万元。七年后,他姐姐的理财本息已经达到了194.8万元,接近最初本金的两倍。第12年的时候,她的本息已经达到了314万元,是最初的3倍多,这就是复利的魅力。
威廉·配第导师打断了王一的回忆,接着对大家说:“5万元,相信每个家庭都会有这些储蓄。如果将这5万元投入到一项每年获10%利率的投资上去。按照复利计算,30年后,当初的5万元资产将变成: F =50000×(1+10%) 30-1 ,也就是将近80万元。这难道不诱人吗?”
威廉·配第导师的例子,让台下的学生们两眼放光,也让王一想到了爱因斯坦的一句话:“宇宙间最大的能量是复利,世界的第八大奇迹是复利,复利的威力比原子弹更可怕。”
“当然了,经济学是聪明人的游戏,复利的确是暴利,但是,”威廉·配第导师笑着说,“作为我的学生,你们可一定要分清暴利和伪装成暴利的骗局,如果你们被传销集团骗去,可不要说是我的学生哦。”
王一和其他学生立马要求道:“导师,快给我们讲讲经济学里的骗局吧!传销到底是怎么回事呢?”