下载掌阅APP，畅读海量书库
立即打开
神经元兴奋总是伴随膜电位的变动（感受器电位、轴突动作电位和突触电位等）。变动的速度有快有慢、持续可长可短，但其基本机制相同，都以神经膜对离子通透性的变化为基础。
同其他可兴奋膜一样，轴突膜内外侧之间在离子组成上虽有相似之处，但却存在着显著的浓度差和电位差。这种差异为产生动作电位提供势能。
轴突静息电位为60～90mV（外正内负）。在负脉冲作用下，高阻抗的轴突膜两侧产生电压差。弱刺激引起的电压差与刺激脉冲的大小成比例并呈指数式升降，一旦刺激强度达到临界值，即使迅速切断电流，轴突膜两侧也可自动地产生一个更大的、外负内正的电变化——动作电位。
在将轴突膜视为欧姆电阻的情况下，利用电压钳技术，可在许多不同的膜电位水平测出Na
+
电流和K
+
电流的数值。根据欧姆定律可计算出各个水平时膜的电阻值（
R
），并以其倒数（1
/R
）或用有关离子所受的推力（
ε
m
-
ε
i
）去除离子电流（
I
i
）所得的商数——电导（
g
i
），作为轴突膜离子通透性的直接指标。Hodgkin学派主要证明的事实是：
g
Na
、
g
K
均随
ε
m
变化，是
ε
m
的函数，并均在正电位时饱和，达最大值；
g
Na
、
g
K
的最大值（
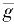Na
、
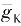）乘以随时间变化、由0到1的无量纲的因数（
m
、
h
、
n
），可以得到电压固定期间任一瞬间的
g
Na
、
g
K
值（
g
Na
＝
·
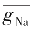m
3
h
，
g
K
＝
·
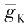n
4
），并得知其为时间的函数。根据离子电导值及其与时间经过特征有关的时间常数和速度常数，Hodgkin、Hux-ley整理出一系列常微分方程。