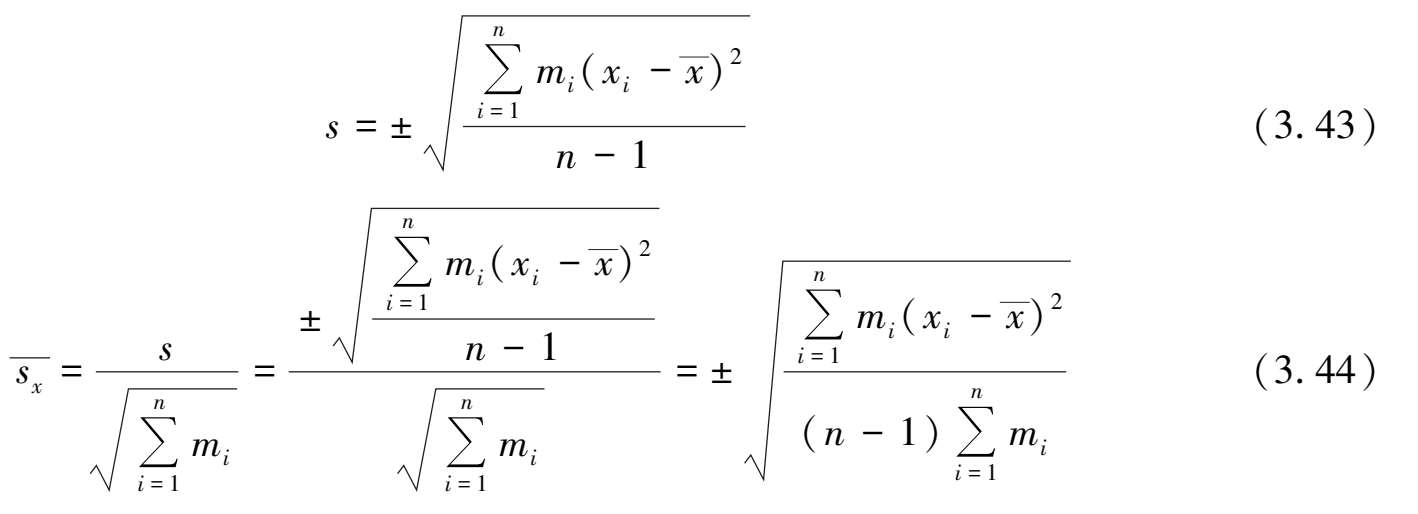在测量中,使待测量与标准量直接比较而得到测量值称为直接测量。通过仪器直接测试读数得到的数据,如测温度、压力;测长度、质量;电流、电压值。
对于实验中的单次测量值,即一次测量度数值,其误差分析有两种方法:
①仪器上没有说明误差范围,按其最小刻度的 1 /2 作为误差。
例如,如图 3.3 所示,用直尺测量某一物体。直尺的最小刻度为 1 mm,表明该直尺有把握的最小测量长度是 1 mm,所以其绝对误差为 1 /2 = 0.5 mm。
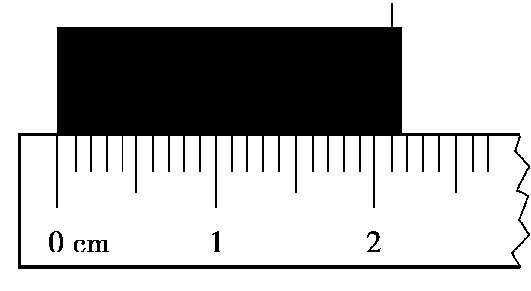
图 3.3 用直尺测量某一物体
②仪器上有误差范围,按给定的误差范围分析计算。
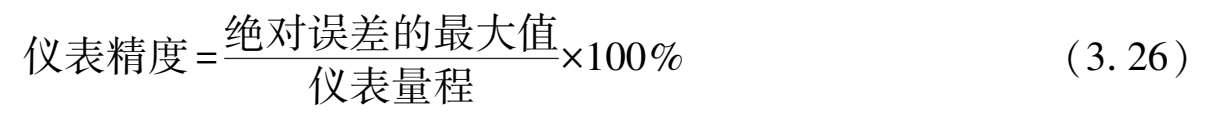
例如,某仪器精度为 0.5 级(±0.5%)(相对误差)当量程 3.2 mg时,绝对误差最大值为:
实际值:测量值±0.016 mg。
重复多次测量值误差,通常采用算术平均误差。
①算术平均误差:是测量值与算术平均值之差的绝对值的算术平均值,表示为:

式中Δ x ——算术平均误差;
x i ——测量值;
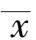 ——全部测量值的平均值;
——全部测量值的平均值;
n ——测量次数。
求算术平均误差时,偏差可能为正也可能为负,所以一定要取绝对值;算术平均误差可以反映一组实验数据的误差大小,但无法表达出各实验值间彼此符合程度。
②标准偏差:标准差也是一种平均数,标准差能反映一个数据集的离散程度。各数据偏离平均数的距离(离均差)的平均数,也称为均方差,用 σ 表示。当实验次数为有限时,把 n 个残差求平方和,除以 n -1 再开方,就称为测量列的标准偏差。当实验次数 n 无穷大时,称为总体标准差 σ ,它常用来表示实验值的精密度:标准差越小,实验数据精密度越好,其定义为:
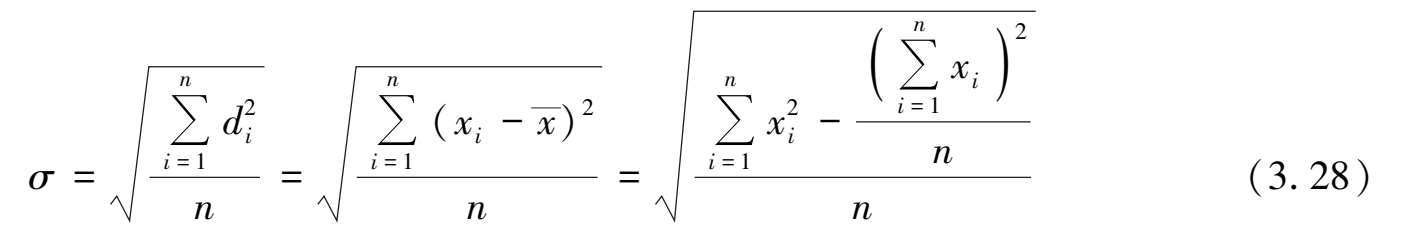
标准差与每一个数据有关,而且对其中较大或较小的误差敏感性很强,能明显反映出较大的个别误差。
【例3.6】 两次测试的偏差分别为:+4,+3,-2,+2,+4;+1,+5,0,-3,-6,求它们的算术平均误差及偏差。
解 :算术平均误差:
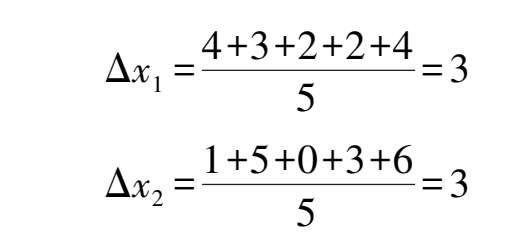
偏差:
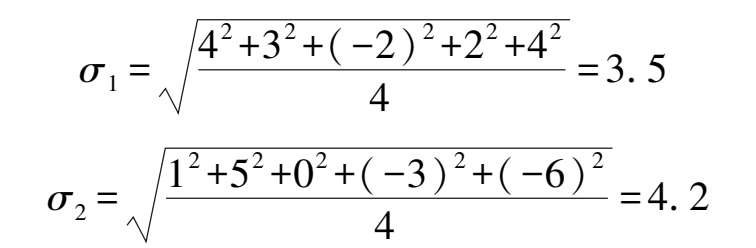
结果表明,标准差越小,实验数据精密度越好,反映仪表越精密。标准差反映了数据的分散性,即随机误差的大小。
(1)算术平均误差
由于真值不易测得,几乎所有的测量中都以最大或然值(即出现此值的概率最大)作为最佳值代替真值。
在一组测量中,如果测量的全部条件相同,那么各个观测值都是同样可信、可取的,各个真值相互之间是等价的;也就是说,它们的权是相同的,称这样的测量为等精度测量,凡标准误差 s 相同的测量都称为等精度测量。
设
a
为某测量的最佳值,而各个量值为
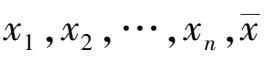 为各测量值的算数平均值,则各值与最佳值间的算术平均值的误差为:
为各测量值的算数平均值,则各值与最佳值间的算术平均值的误差为:

取 n 个误差的和:

根据误差的抵偿性,当次数
n
很大时,
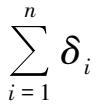 =0,则
=0,则

所以,
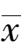 就是最可信赖的最佳值,而
就是最可信赖的最佳值,而
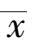 正是算术平均值,因此,在等精度测量中,算术平均值为最能近似代表真值的最佳值。
正是算术平均值,因此,在等精度测量中,算术平均值为最能近似代表真值的最佳值。
(2)有限观测次数中标准误差 s 的计算
设真值为
a
,算数平均值为
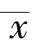 ,各观测值为
x
i
,则有
,各观测值为
x
i
,则有

均值的误差:

将式(3.33)求和得:

根据误差的抵偿性,当次数
n
很大时,
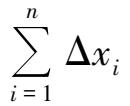 =0,则
i
= 1
=0,则
i
= 1

将式(3.33)平方后求和得:
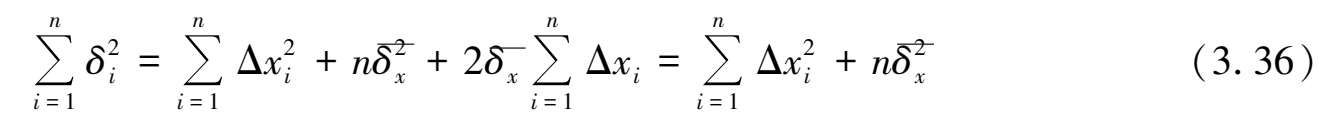
将式(3.35)平方后得:
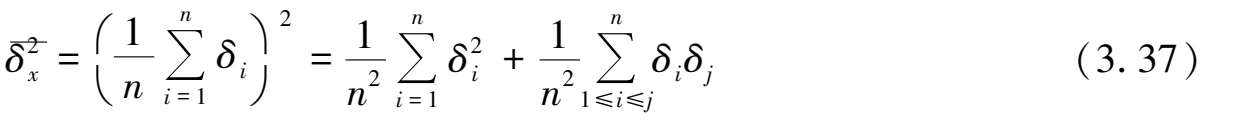
当次数
n
很大时,可认为
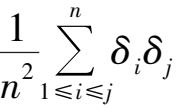 =0,则
=0,则
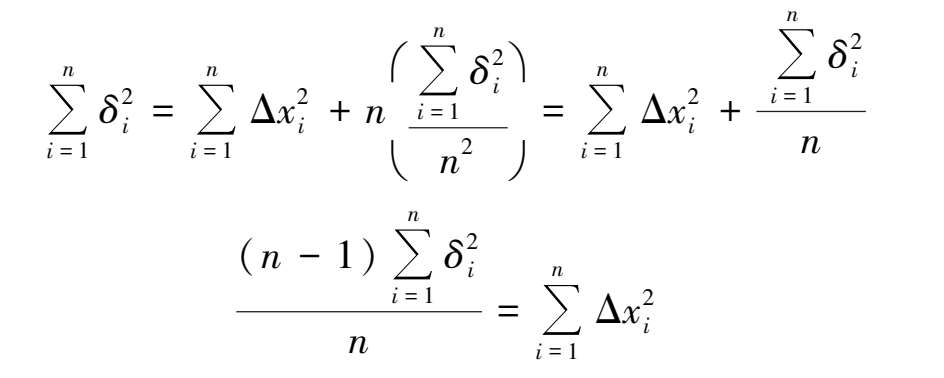
所以
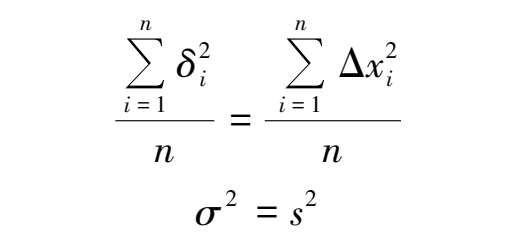
即
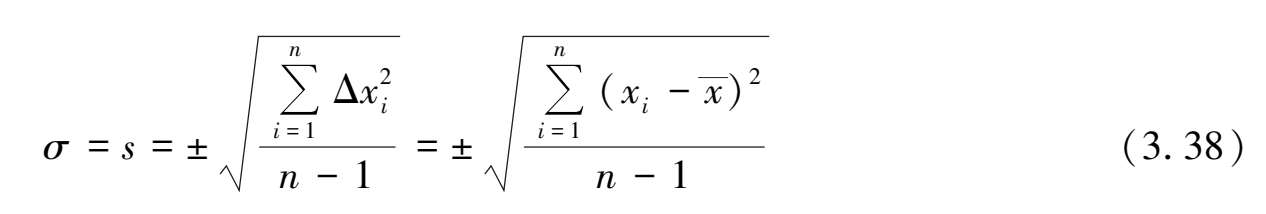
这说明在有限次观测中,各观测值与算术平均值之差的平方和除以测量次数减 1(即
n
-1)的方根等于平方差(标准差)。这由贝塞尔导出,故又称为贝塞尔方程,
σ
表示了测量中约有68.3%的点落在(
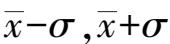 )范围内,
σ
反映了测量的精密性。当
n
很大时,可以认为算数平均值等于真值。这个结论与前面的结论完全一致。
)范围内,
σ
反映了测量的精密性。当
n
很大时,可以认为算数平均值等于真值。这个结论与前面的结论完全一致。
(3)算术平均值的误差
上述方法可以证明,在一组等精度测量中,测量值的算术平均值 x 的标准误差为:
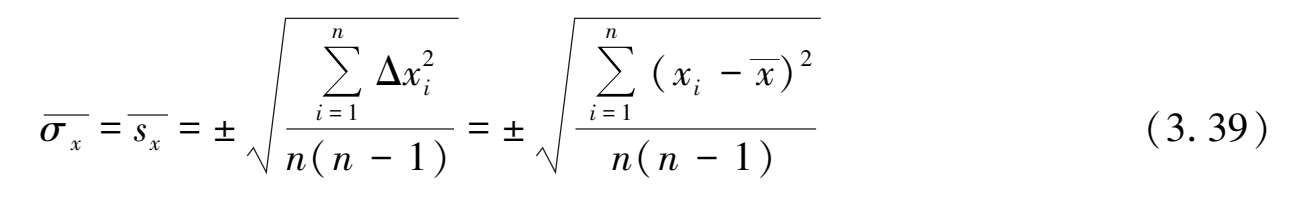
(1)权数
对于一组不等精度的测量值 x 1 , x 2 ,…, x n ;对应的标准误差为 s 1 , s 2 ,…, s n ;对应的权数为 m 1 , m 2 ,…, m n ;每单位权的标准差为 s ,则
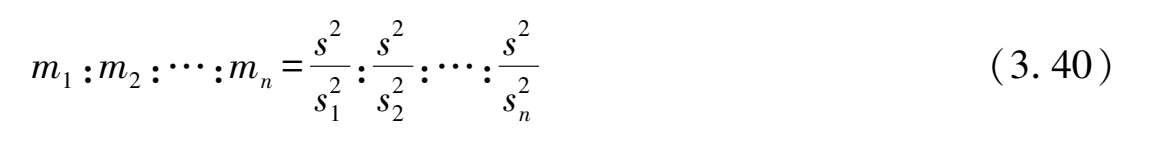
得出:

式(3.41)是根据标准误差计算权的公式,为了计算方便这里 s 通常取 1。
(2)最佳估计值
按上节同样的原理,可得出在不等精度直接测量中
x
i
的最佳估计值为各测量值的加权算数平均值
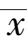 :
:

(3)不等精度测量中的标准误差
s
及算数平均值中的标准误差
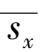
按上节同样的原理,可得出在不等精度直接测量中的标准误差
s
及算数平均值的标准误差
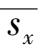 :
: