下载掌阅APP，畅读海量书库
立即打开
在实际测量中，由于偶然误差的客观存在，所得数据总存在一定的离散性，也可能由于过失误差出现个别离散较远的数据，通常称为坏值或可疑值。为将测量中可能存在的坏值剔除，需要进行测量数据的合理性检测。
通常判别坏值的常用方法有两种:
①物理判别法：在观测过程中及时发现并纠正由于仪器仪表、人员及实验条件等情况变化造成的错误。
②统计判别法：规定一个误差范围(± kσ )及相应的置信概率 1- α ,凡超过该误差范围的测量值，都是小概率事件，即判断是粗大误差，认为是坏值而予以剔除。关于 k 值的求解，主要有以下几种方法。
拉伊特方法的基本思想是将测量值看成服从某一分布(按正态分布)的随机变量，以最大误差范围 3 σ 为依据进行判别。
设有一组测量值
x
i
(
i
= 1,2,…,
n
),其子样平均值为
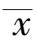,偏差
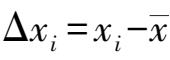,按照贝塞尔公式
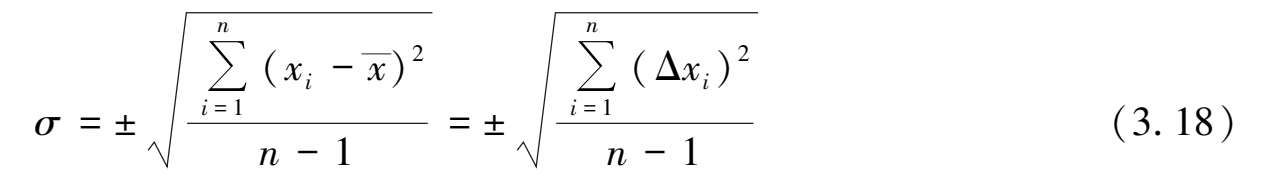
如果测量值
x
i
(1≤
i
≤
n
)的偏差
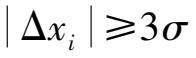时，则认为
x
i
是含有粗大误差的坏值。
该方法的最大优点是简单、方便、不需要查表。但对小子样不准，往往会把坏值隐藏下来。例如，当 n ≤10 时,
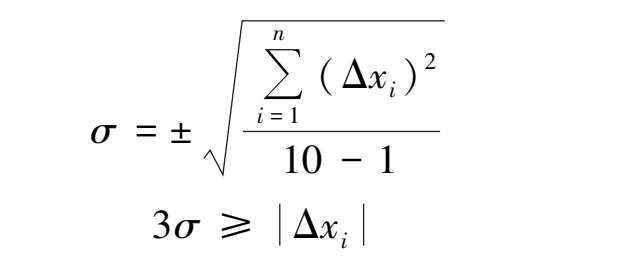
此时，任意一个测量值的偏差Δ
x
i
都能满足
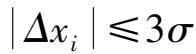,不可能出现大于 3
σ
的情况。在一些要求严格的场合，也用 3
σ
判别，但
n
≤5 的测量同样无法剔除坏值。
【例3.3】 对某物理量进行 15 次等精度测量，测量值为:28.39,28.39,28.40,28.41,28.42,28.43,28.40,28.30,28.39,28.42,28.43,28.40,28.43,28.42,28.43;试用拉伊特方法判断该测试数据的坏值，并剔除。
解 :测量值见表 3.5。
表3.5 测量值
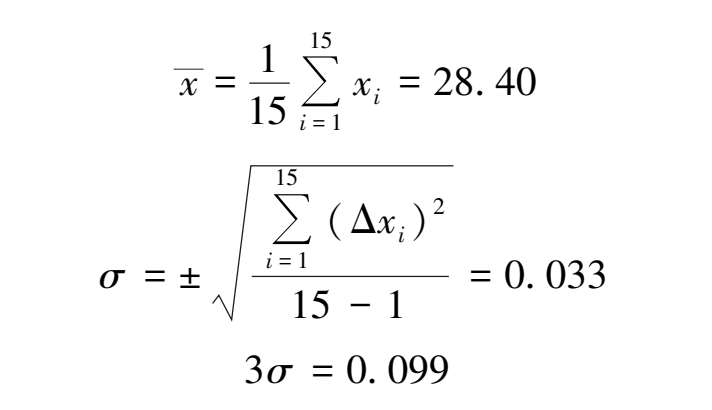
这组数据最大值 x max = 28.43;最小值 x min = 28.30。
最大值偏差为：Δ x 6 = 28.43-28.40 = 0.03
最小值偏差为：Δ x 8 = 28.30-28.40 = -0.10
由拉伊特方法可知，Δ x 8 = -0.10,不在(-0.099,0.099)内, x 8 = 28.30 是坏值，应剔除。
肖维勒方法的基本原理认为，在 n 次测量中，坏值出现的次数为 1 /2 次，即坏值出现的概率为 1 /(2 n )。按概率积分:
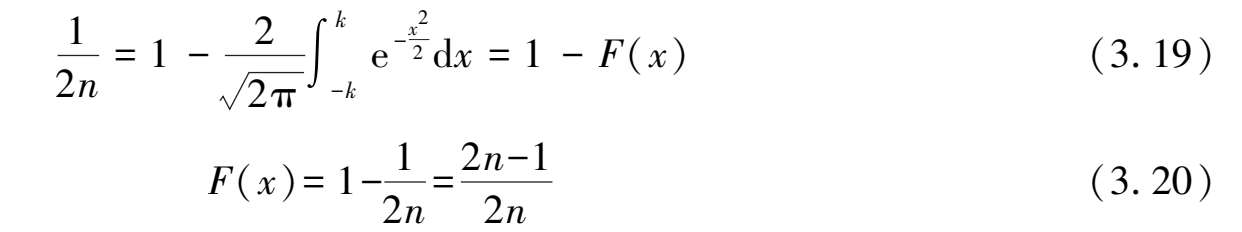
不同的
n
可计算
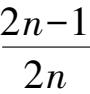的值，查概率积分表，可以求出
k
。
对于一组观测值，其中的离差值Δ x i 大于或等于 k ( n , σ ) σ 者为坏值，应予剔除。肖维勒方法中的系数 k 与 n 的关系对照见表 3.6。
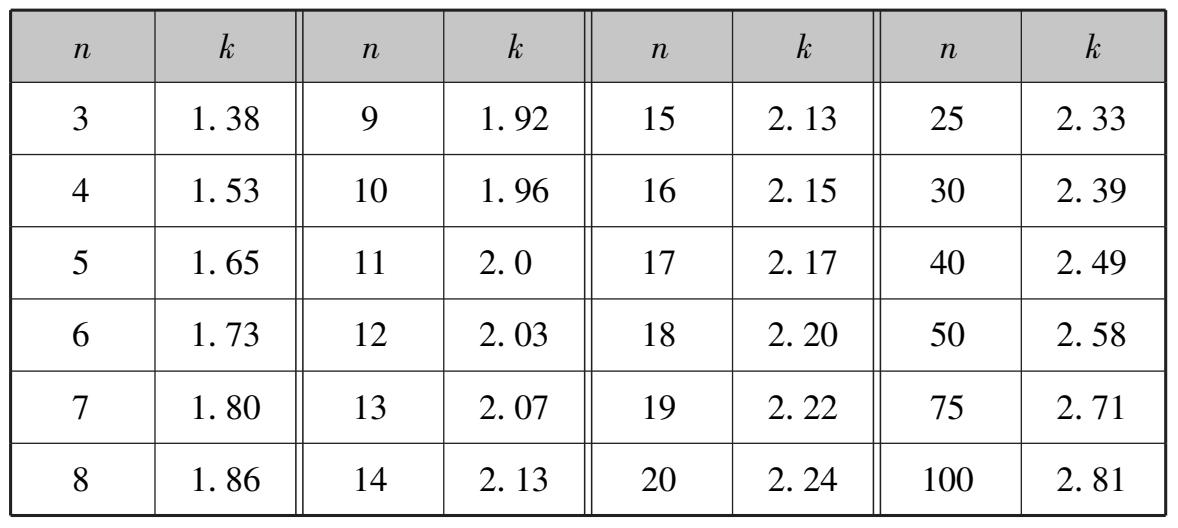
表3.6 肖维勒方法中的系数k与n的关系对照表
当测量次数较小时，按 t 分布的实际误差分布范围来判断粗大误差较为合理。 t 检验方法的原则是：首先剔除一个与均值偏离最大的数据，然后对剩余的数据进行统计计算，以判定该次剔除是否合理，即判定已被剔除的那个数据是否含有粗大误差。
对于某一等精度重复测量 x 1 , x 2 ,…, x n ,若认为其中的某数据 x j 为可疑数据，将其剔除后的平均值为(计算时不包括 x j ):
将其剔除后的样本标准偏差为(计算时不包括
)
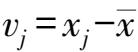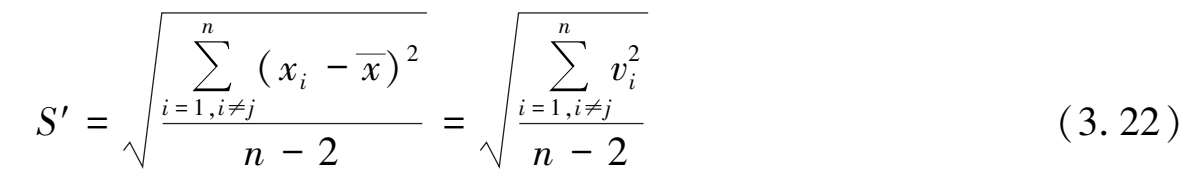
根据测量次数 n 和选定的显著性水平 α ,即可由表(3.7)查得 t 检验系数 K α ( n ),若
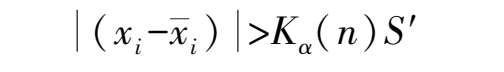
则认为测量值 x j 含有粗大误差，剔除它是正确的。否则，就认为 x 不含有粗大误差，应予以保留。
表3.7 t检验系数K α (n)表
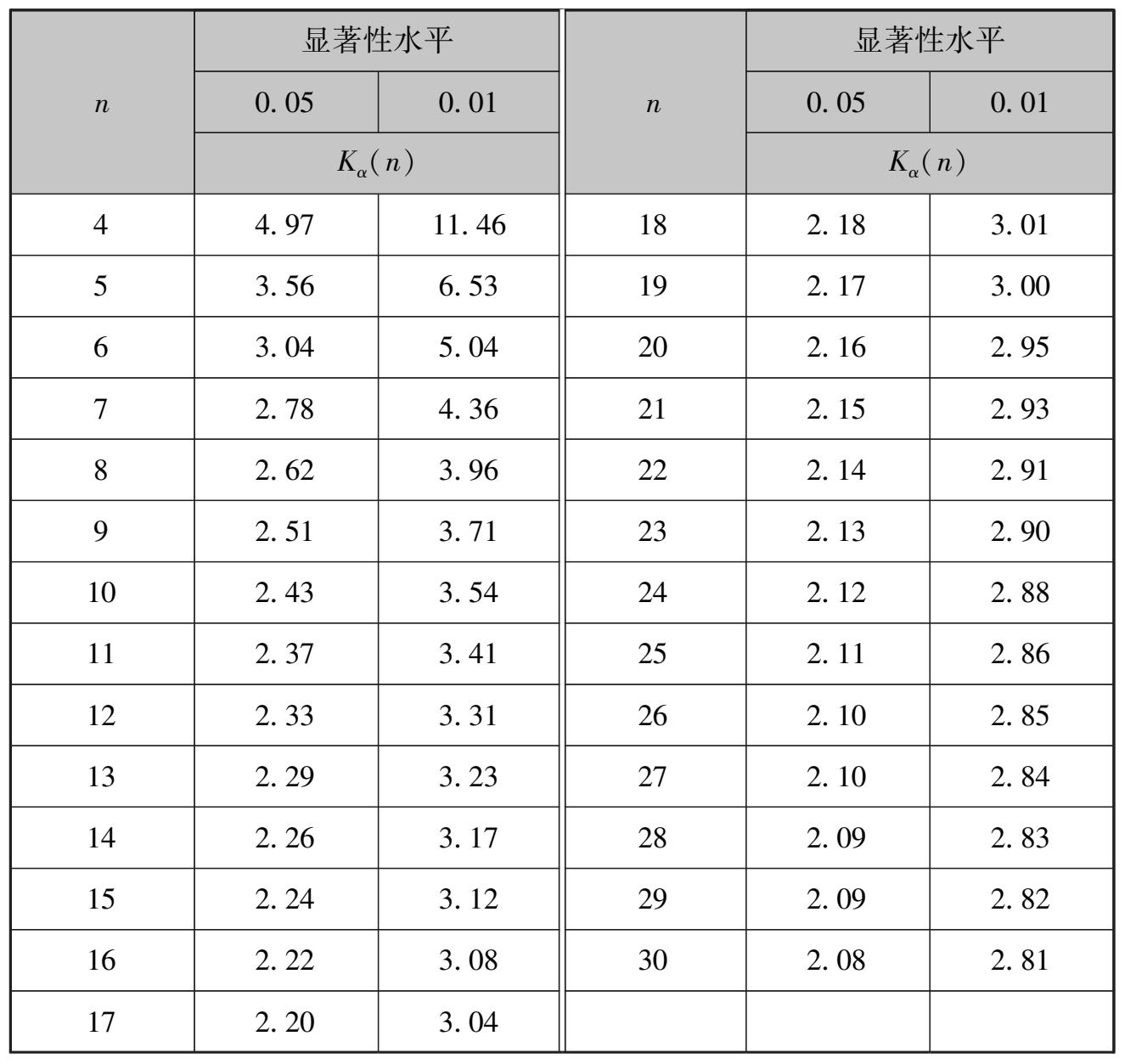
采用 t 检验准则判断测量数据列 x 1 , x 2 ,…, x n 中是否有数据含有粗大误差的计算步骤如下:
①计算样本均值
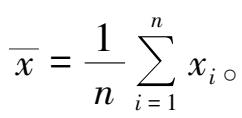
②剔除一个与均值
x
偏差(即残差)最大的数据
x
后，根据式子计算剩下的
n
-1 个数据的样本均值
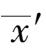与标准偏差
S′
。
③根据测量次数 n 和选定的显著性水平 α ,查 t 检验系数表得到 K α ( n )。
④如果
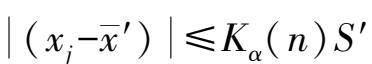,则该数据不应剔除，判断结束。如果
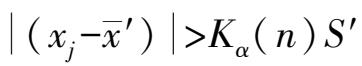,则该数据有粗大误差，所做的剔除是正确的。尚需对剩下的
n
- 1 个数据继续进行判断。
⑤在剩下的
n
-1 个数据中剔除一个与均值
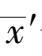偏差最大的数据
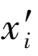,然后计算余下的
n
-2 个数据的样本均值
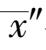与标准偏差
S″
。
⑥根据测量次数
n
-1 和选定的显著性水平
α
,查
t
检验系数表得到
K
α
(
n
-1)。如果
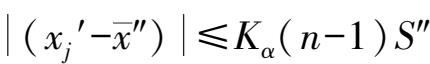,则该数据不应剔除，判断结束。如果
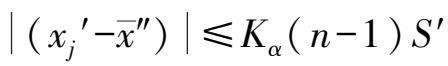,该数据有粗大误差，所做的剔除是正确的。尚需对剩下的
n
-2 个数据继续进行判断，这样一直进行下去，直到找不到含有粗大误差的测量数据为止。
格拉布斯方法的原理是用显著水平
α
来计算
k
值。这里把误差超过±
kσ
的概率称为显著水平
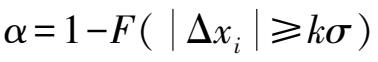,这样式(3.20)变为:
或
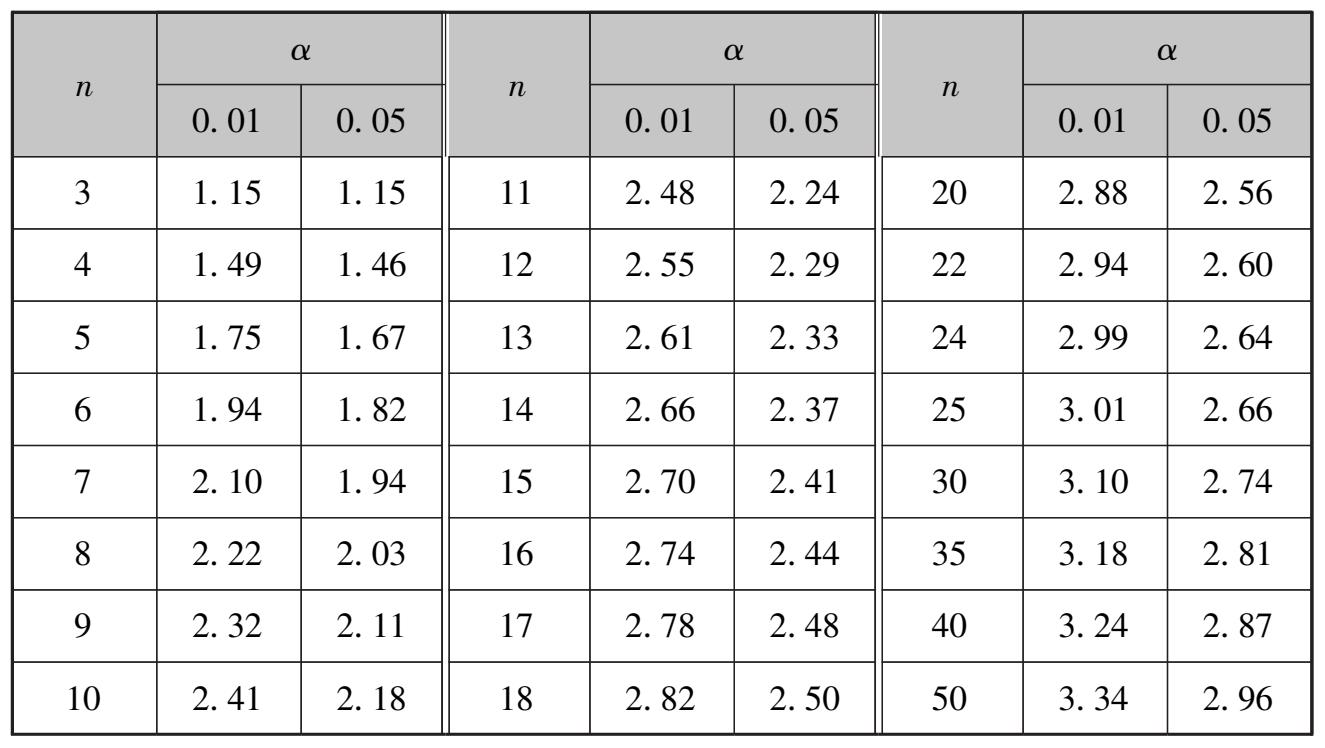
在大多数情况采下用的显著水平为 0.01 或 0.05(即有 1%或 5%的概率超出范围 kσ ),对精度较高的测量一般都有 α = 0.01。 k 由观测次数 n 和 α 所决定，列于表 3.8。
表3.8 格拉布斯方法中的k(n,α)
采用格拉布斯方法判断测量数据的步骤如下:
①数据排序。
②计算包括可疑值在内的平均值及标准偏差 σ 。
③从表中查取 k ( α , n )。其中 α 为显著性水平，表示检验出错的概率 α = 0.01,0.05;1- α 置信度，置信水平。
④计算偏差绝对值。
⑤选取偏差绝对值最大的数据来检验，如果满足以下条件则剔除:
①可疑数据应逐一检验，不能同时检验多个数据。
②剔除一个数后，如果还要检验下一个数，则应注意实验数据的总数发生了变化。
③根据测量次数 n ,确定判别过失误差的准则:
【例3.4】 以例 3.3 中的数据，用格拉布斯方法判断是否存在坏值( α = 0.05)。
解 :
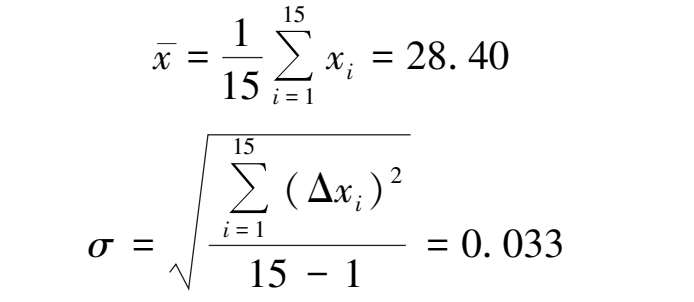
当 n = 15,查表 3.8 得 k = 2.41, k · σ = 2.41×0.033 = 0.080
这组数据最大值 x max = 28.43;最小值 x min = 28.30
最大值偏差为：Δ x 6 = 28.43-28.40 = 0.03
最小值偏差为：Δ x 8 = 28.30-28.40 = -0.10
由格拉布斯方法可知：Δ x 8 = -0.10 不在区间范围(-0.080,0.080), x 8 = 28.30 是坏值，应剔除。
【例3.5】 使用毕托管对风道内某点气流速度进行测量，测量值根据大小规律为:
7.890,7.956,7.970,7.976,7.978,7.987,7.995,8.006,8.010,8.018,8.020,8.039,8.048,8.063,9.101。
取 α = 0.01,用格拉布斯方法判断是否存在坏值。
解 :平均值:
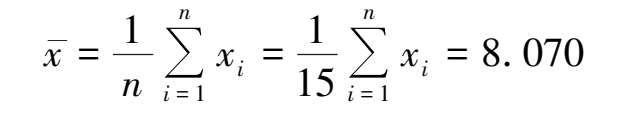
标准差:
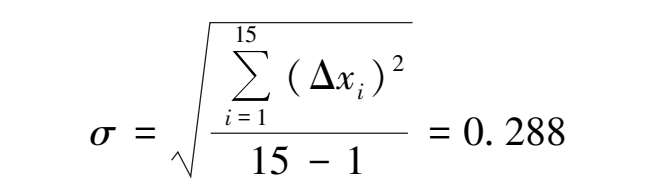
查表 3.8 得:
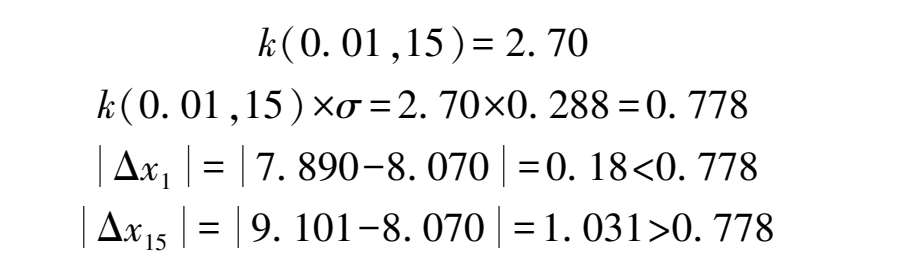
因此,7.89 不是坏值,9.101 是坏值；除去这一数据后, n = 14,再按同样的方法计算并判断 x 1 和 x 14 ,直到正常为止。本例中的 x 1 和 x 14 均为正常值，判断过程不再重复。利用这种办法判断坏值时，只要测量列中残余误差过大的测量值均可被判剔除，而不管坏值产生是人为的还是意外干扰所致，这在合理性检验时务必注意。