




用子样观测值推断总体的参数特征属于统计推断的范畴,包括两方面的内容:参数估计和统计检验。
由于实验研究工作的需要,往往先要对总体的某一统计特征进行假定,之后利用反复观测的子样数据,根据概率统计进行计算,以判断假设是否成立,这就是统计检验或假设检验。
u 检验是一般用于大样本(即样本容量大于 30)平均值差异性检验的方法。它是用标准正态分布的理论来推断差异发生的概率,从而比较两个平均数的差异是否显著。
当已知标准差时,验证一组数的均值是否与某一期望值相等时,用 u 检验。另外,对于 u 检验国外的统计学教材大多采用 Z 检验的说法。而国内统计学书籍,大多采用 u 检验。
1)总体均值的一致性检验
(1)双边检验
设总体
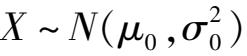 ,子样观测值
x
1
,
x
2
,…,
x
n
,检验假设
H
0
:
μ
=
μ
0
(
μ
0
为已知常数),子样均值服从正态分布
,子样观测值
x
1
,
x
2
,…,
x
n
,检验假设
H
0
:
μ
=
μ
0
(
μ
0
为已知常数),子样均值服从正态分布
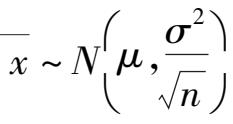 标准化可以得到统计量
标准化可以得到统计量

对于给定的信度
α
,可根据正态分布密度函数,查到
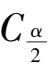 ,使:
,使:

子样观测值计算
u
0
,如有
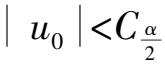 ,则接受原假设检验,否则拒绝。
,则接受原假设检验,否则拒绝。
在实际检验中,人们往往感兴趣的是在采用新工艺或新参数配比后,总体的均值有显著增大,例如相变材料的强度、产品的使用寿命、空调设备的效率等指标无疑是越高越好的,而成本、原料消耗等指标应尽可能地小一些,这一类问题的处理涉及单边检验。
(2)右边检验
在这种情况下,将检验新的总体均值
μ
是否比原总体均值
μ
0
大,即在显著水平
α
下,检验假设
H
:
μ
≥
μ
0
,当
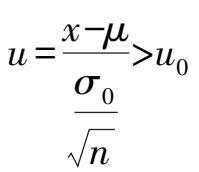 时接受假设,反之否定原假设,此时认为总体均值
μ
比原均值
μ
0
显著地增大了。
时接受假设,反之否定原假设,此时认为总体均值
μ
比原均值
μ
0
显著地增大了。
(3)左边检验
同样,在显著水平
α
下,将检验新的总体均值
μ
是否比原总体均值
μ
0
小,即在显著水平
α
下,检验假设
H
:
μ
≤
μ
0
,当
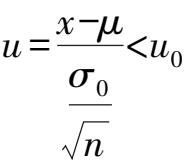 时接受假设,反之否定原假设,此时认为总体均值
μ
比原均值
μ
0
显著地减小了。
时接受假设,反之否定原假设,此时认为总体均值
μ
比原均值
μ
0
显著地减小了。
2)两个总体均值的一致性检验
u 检验可以来检验两个遵守正态分布,标准偏差不相等的总体均值是否有显著性差异,即检验假设 H : μ 1 = μ 2 。
设两总体为
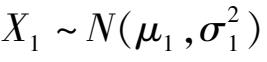 和
和
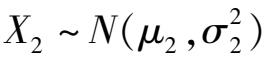 ,已知
,已知
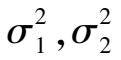 ,检验假设
H
0
:
μ
1
=
μ
2
。
,检验假设
H
0
:
μ
1
=
μ
2
。
分别取来自两个总体的容量为
n
1
和
n
2
的子样,子样平均值
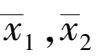 ,其
u
值计算公式为:
,其
u
值计算公式为:
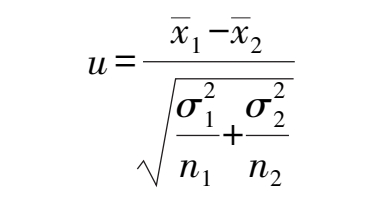
在显著水平
α
下,检验
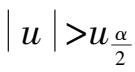 时,否定假设
H
:
μ
1
=
μ
2
,即认为两总体均值存在显著性差异。同样也可以对
μ
1
和
μ
2
进行单侧检验。
时,否定假设
H
:
μ
1
=
μ
2
,即认为两总体均值存在显著性差异。同样也可以对
μ
1
和
μ
2
进行单侧检验。
右边 u 检验:原假设 μ 1 ≤ μ 2 ,当 u > u α 时否定原假设。
左边 u 检验:原假设 μ 1 ≥ μ 2 ,当 u <- u α 时否定原假设。
t 检验也称Student t 检验(Student’s t test),主要用于样本含量较小(如 n <30),总体标准差 σ 未知的正态分布检验。
设总体 X ~ N ( μ , σ 2 ), σ 未知,子样观测值 x 1 , x 2 ,…, x n ,检验假设 H 0 : μ = μ 0 ( μ 0 为已知常数)。
总体标准差未知,只能用子样标准差取代,将统计量定义为:

若
H
0
成立,则
t
分布服从自由度为
n
-1 的
t
分布,按给定的置信度
α
,可以查出
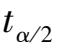 ,使
,使
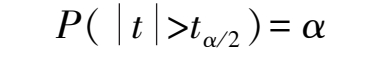
由子样计算得到的统计量 t > t α/2 时,否定原假设,否则接收。同样可以用 t 检验来判断两个正态总体的均值的差。
设两总体为
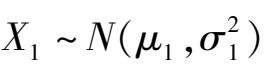 和
和
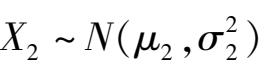 ,已知
,已知
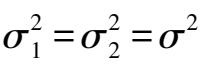 ,但数值未知,需要检验假设
H
0
:
μ
1
=
μ
2
。
,但数值未知,需要检验假设
H
0
:
μ
1
=
μ
2
。
因总体方差未知,故用子样方差的加权平均值取代:
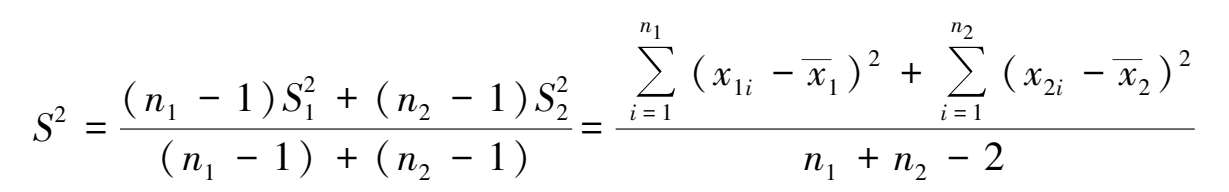
作统计量
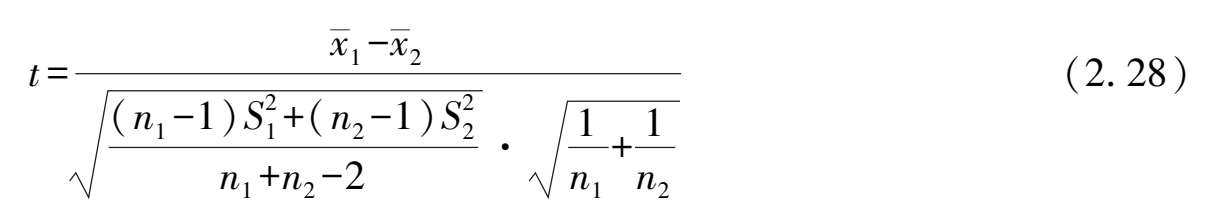
若原假设 H 0 成立,可以证明,统计量 t 服从自由度为 n 1 + n 2 -2 的 t 分布,因此给定置性度 α 下进行 t 检验。
在显著水平下,按照总自由度
f
=
n
1
+
n
2
-2 及
α
查
t
分布表(附录 4),确定拒绝域临界点
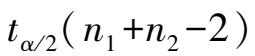 ,当
,当
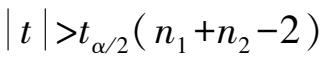 时,否定假设
H
0
:
μ
1
=
μ
2
,进行单边检验的方法和步骤同
u
检验法。
时,否定假设
H
0
:
μ
1
=
μ
2
,进行单边检验的方法和步骤同
u
检验法。
如果 n 1 和 n 2 都比较大,则可以用下式近似计算统计量 t :

这里的
n
1
和
n
2
不一定相等,但最好不要相差太大,在显著性水平
α
下,当
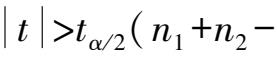
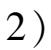 时,否定假设。
时,否定假设。
当需要检验总体方差时,则应利用 χ 2 分布的统计量。
设总体
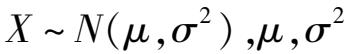 均未知,子样观测值
x
1
,
x
2
,…,
x
n
,检验假设
H
0
:
σ
=
σ
0
(
σ
0
为已知常数)。
均未知,子样观测值
x
1
,
x
2
,…,
x
n
,检验假设
H
0
:
σ
=
σ
0
(
σ
0
为已知常数)。
总体标准差
σ
未知,只能用子样标准差
S
取代,被检验假设
H
0
:
σ
=
σ
0
也可以写作
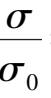 = 1,这样被检验假设可化为检验
= 1,这样被检验假设可化为检验
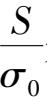 是否接近 1 的问题,于是统计量定义为:
是否接近 1 的问题,于是统计量定义为:
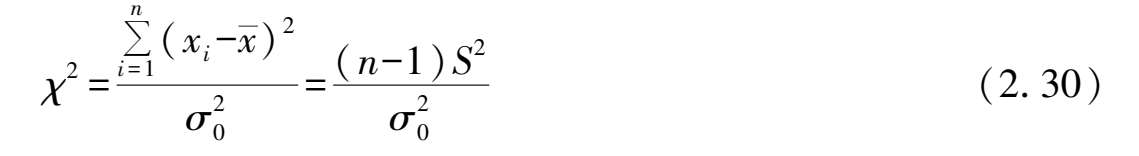
公式的比值具有上限和下限,查表时应注意使 χ 2 满足:

这是因为若假设 H 0 成立,值必定在上限和下限值之间,否则即舍弃原假设 H 0 。
F 检验用于检验二项正态总体方差的齐性。
设二项正态总体
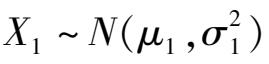 和
和
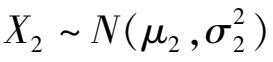 ,其中
μ
1
,
μ
1
,
σ
1
,
σ
2
均未知。若已知两个总体的子样分别为
,其中
μ
1
,
μ
1
,
σ
1
,
σ
2
均未知。若已知两个总体的子样分别为
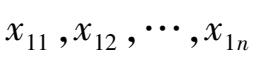 和
和
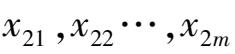 ,要求检验假设
H
0
:
σ
1
=
σ
2
。
,要求检验假设
H
0
:
σ
1
=
σ
2
。
由于
σ
1
,
σ
2
均未知,若判断
σ
1
=
σ
2
,只能用二子样方差取代,问题归结为比较
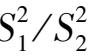 的问题,所以应从
的问题,所以应从
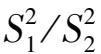 出发就构造统计量:
出发就构造统计量:

F 服从第一自由度为 n -1,第二自由度为 m -1 的 F 分布,记作 F ~ F ( n -1, m -1)。
按照给定的置信度 α ,根据自由度( n -1, m -1),可以通过查表查出上限值,使
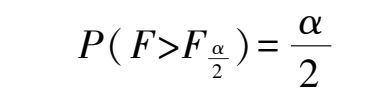
查下限时,
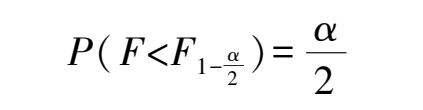
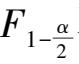 不能直接提供,需做变换,使
不能直接提供,需做变换,使
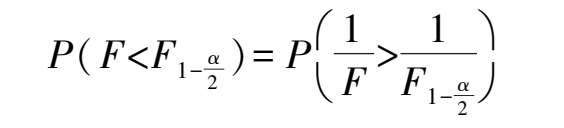
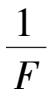 ~
F
(
m
-1,
n
-1),查表得到
~
F
(
m
-1,
n
-1),查表得到
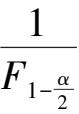 ,即可得出
,即可得出
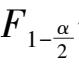 值。
值。