下载掌阅APP，畅读海量书库
立即打开
定义：设总体X的分布函数F(x,θ)含有未知参数θ，对于给定值α(0<α<1),若由样本(
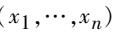确定的两个统计量
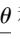和
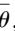使
称区间
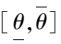为参数θ的置信区间，一个下限，一个上限，可置信水平 1-α，含义就是此区间包含真值的概率为 1-α，置信系数为α。
【例2.1】 母体正态分布N(μ，σ 2 ),求均值的置信水平区间 1-α，α= 0.05。
解
:对于
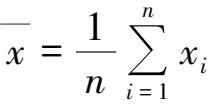这个无偏的最小方差估计子，将其规范化为:
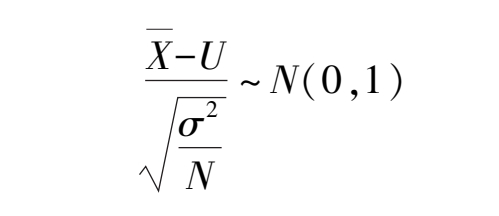
那么
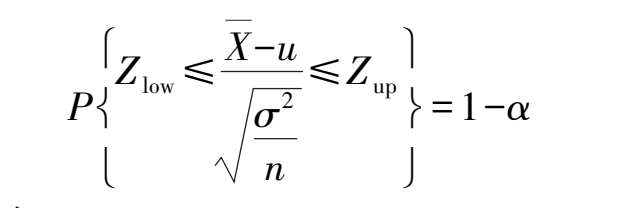
区间[ Z low , Z up ]有很多，比如
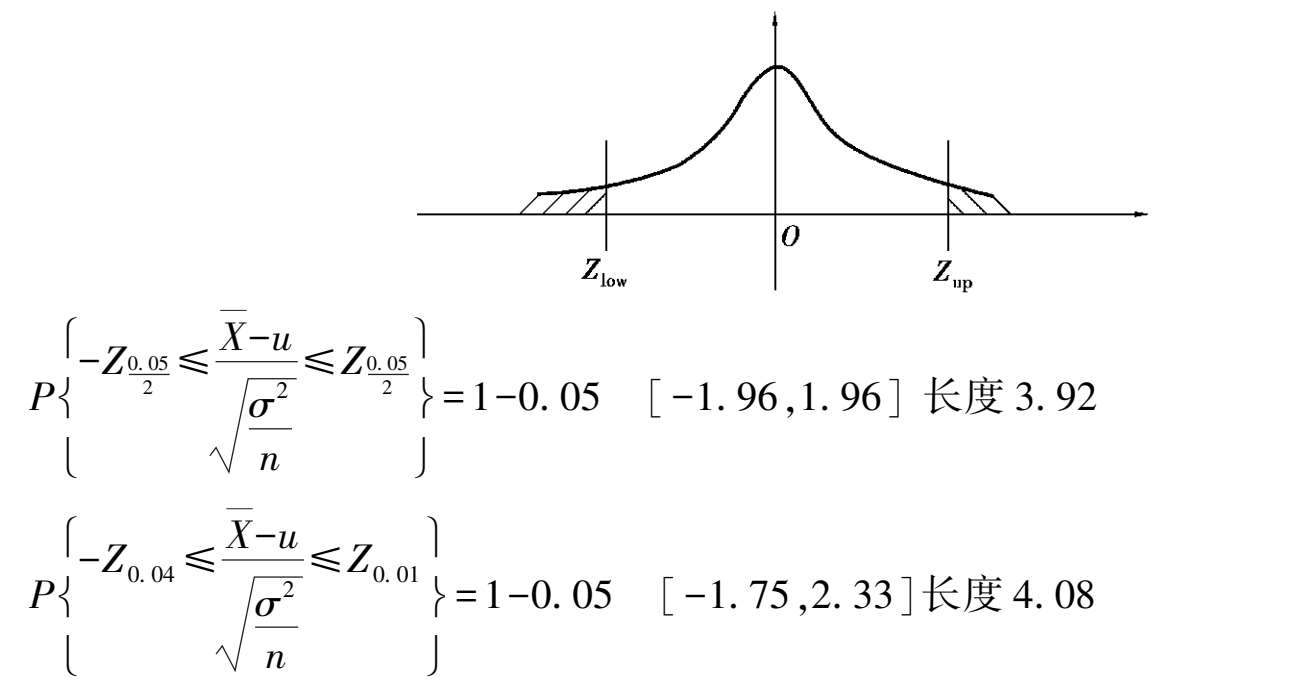
两种都满足，这里[ Z low , Z up ]就是前面的上 α 分位，可以查表。但是还是第一种对称的区间长度小，精确度高，所以用第一种。
当方差未知，则用估计量代替方差,
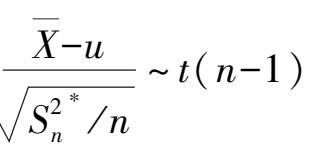,那么去查
t
分布表。
当方差未知，方差的置信区间
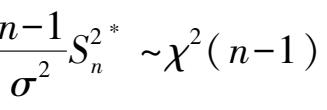,查卡方分布表，由于分布不对称，那么区间为
。
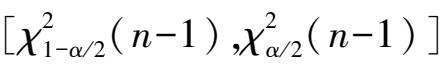对于两种母体的分布形式，在数理统计书籍中有相关统计量及其查阅方法。还有就是单侧置信区间的
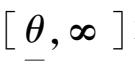和
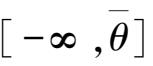两种，不外乎也是查表。