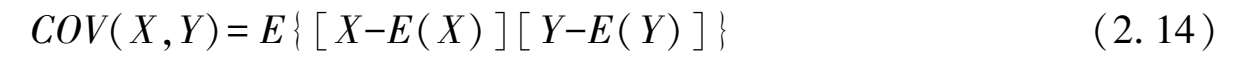2.2 随机变量的数字特征

对于随机变量，可以用理论分布完整地描述其特征，然而在实际工程中，一方面随机变量 X 的概率分布不易得知；另一方面有些场合并不要求用概率分布来描述随机变量，只需知道随机变量变化值的集中位置和离散程度即可。本小节简要介绍随机变量的数字特征。

2.2.1 期望值与方差

1)数学期望

定义随机变量 X 的数学期望为:

显然，数学期望对于峰面对称的密度函数来说，就是曲线峰值的位置。

对于离散型随机变量 X ,数学期望:

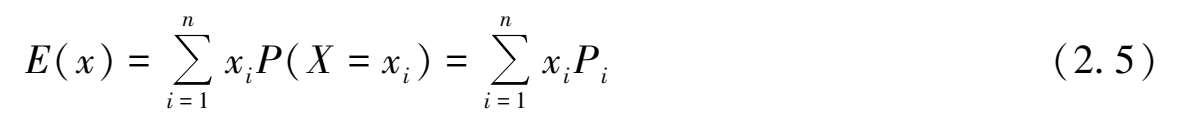
由定义可知，数学期望为随机变量的值以其相应概率的加权平均值。

2)方差

定义随机变量 X 的方差为:

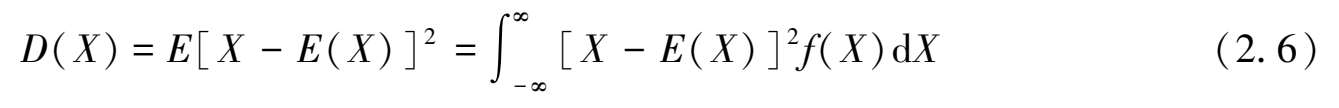
对于离散型随机变量 X ,其方差:

方差的平方根称为标准差或均方差，记为:

从方差定义可以看出，它是随机变量 Y = [ X - E ( X )] ² 的数学期望。对于确定的分布, E ( X )是确定的，因而，方差是反映 X 与 E ( X )偏离程度的变量 Y 的期望值，是描述随机变量 X 分散性的特征参数。

2.2.2 变异（变差）系数

从方差是以随机变量的数学期望为标准，是有量纲的。为了克服量纲不同，不便于方差比较的弊端，引出一个无量纲的变异系数，定义为:

用以描述随机变量 X 的相对离散程度。

2.2.3 矩

随机变量 X 对 c 的 k 阶矩记为 E ( X - c ) ^k ,定义为:

式中 c ——任意常数;

k ——任意正整数。

当 c = 0 时，称为原点矩，以 ν _k 表示 k 阶原点矩。

当 c = E ( x )时，称为中心矩，以 μ _k 表示 k 阶中心矩。

2.2.4 协方差

把 E {[ X - E ( X )][ Y - E ( Y )]}定义为随机变量 X 与 Y 的协方差，记为Cov( X , Y ),即Cov = E {[ X - E ( X )][ Y - E ( Y )]}。

由方差和数学期望性质有等式

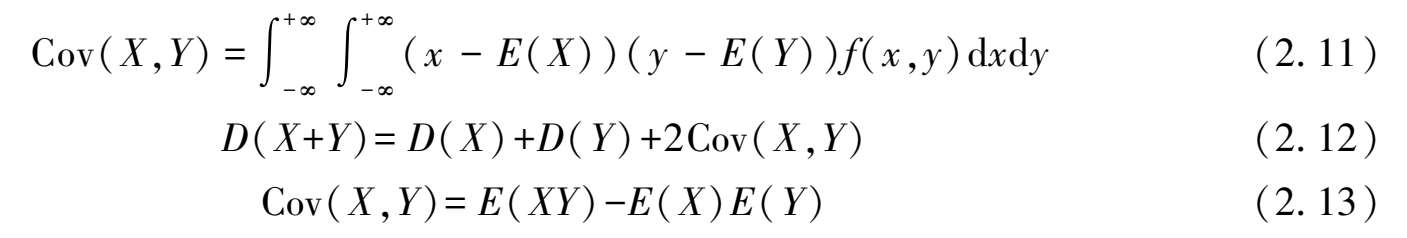
协方差具有下述性质:

①Cov( X , Y )= Cov( Y , X )。

②Cov( aX , bY )= ab Cov( X , Y )。

③Cov( X ₁ + X ₂ , Y )= Cov( X ₁ , Y )+Cov( X ₂ , Y )。

2.2.5 数字特征性质

1)随机变量

①随机变量的常数倍，其数学期望为原期望值的常数倍。

E ( cX )= cE ( X )

② X , Y 为两个相互独立的随机变量，则有:

E ( X + Y )= E ( X )+ E ( Y )

③ X , Y 为两个相互独立的随机变量，则有:

E ( XY )= E ( X ) E ( Y )

2)方差

①常数的方差为 0,即

D ( c )= 0

②随机变量的常数倍，其方差为随机变量 X 方差与常数平方之积。 D ( cX )= c ² D ( X )。

③ X , Y 两个相互独立的随机变量，则 D ( X + Y )= D ( X )+ D ( Y )。

④ X , Y 两个任意的随机变量，则 D ( X ± Y )= D ( X )+ D ( Y )±2 COV ( X , Y )。

其中，为 X , Y 的协方差，可以表示为: 6HLl+tRoUJvdd19F1hqIb30gWcFwOCR8Khim7uW9CrjnJSfAK6ceIKQBrDa9cJlk