





随机振动过程一般都是随时间变化的,随机过程理论是由无限多个样本函数组成的集合。假如有 n 个加速度传感器安装在 n 个车辆上并且行驶在同一条高低不平的道路上,通过传感器测量加速度的变化分别为 a 1 ( t ), a 2 ( t ),…, a n ( t ),车辆通过该道路的加速度也是一个随机过程,这些加速度被称为随机过程的样本函数。这个随机过程可以表示为
假如在某一个时间 t 1 ,随机过程 A ( t )的所有样本函数 a i ( t )在 t 1 时刻的加速度值构成了随机变量,可以表示为 A ( t 1 )={ a i ( t 1 )},此时研究了一个时间点的问题,工程上也将 A ( t 1 )称为随机过程 A ( t )在时间 t = t 1 时刻的状态。因此车辆行驶的随机过程可以又被表示为
整个随机过程是由无限多个样本构成的一个集合,也是随时间发生变化的随机变量集合。因此随机过程有两种统计学方法:一种是平均集合;另一种是平均时间集合。
功率谱密度(PSD)是结构在随机动态载荷激励下响应的统计结果,它是一条体现功率谱密度值和频率值的关系曲线,随机振动过程中,在一定频率范围内激励幅值在不断变化,但激励幅值的均值基本趋于一个相对稳定的常量。随机振动过程的总频率范围可以分解为若干个子频率范围,在每个子频率范围计算二次方和的平均值,如图1-3-1所示。
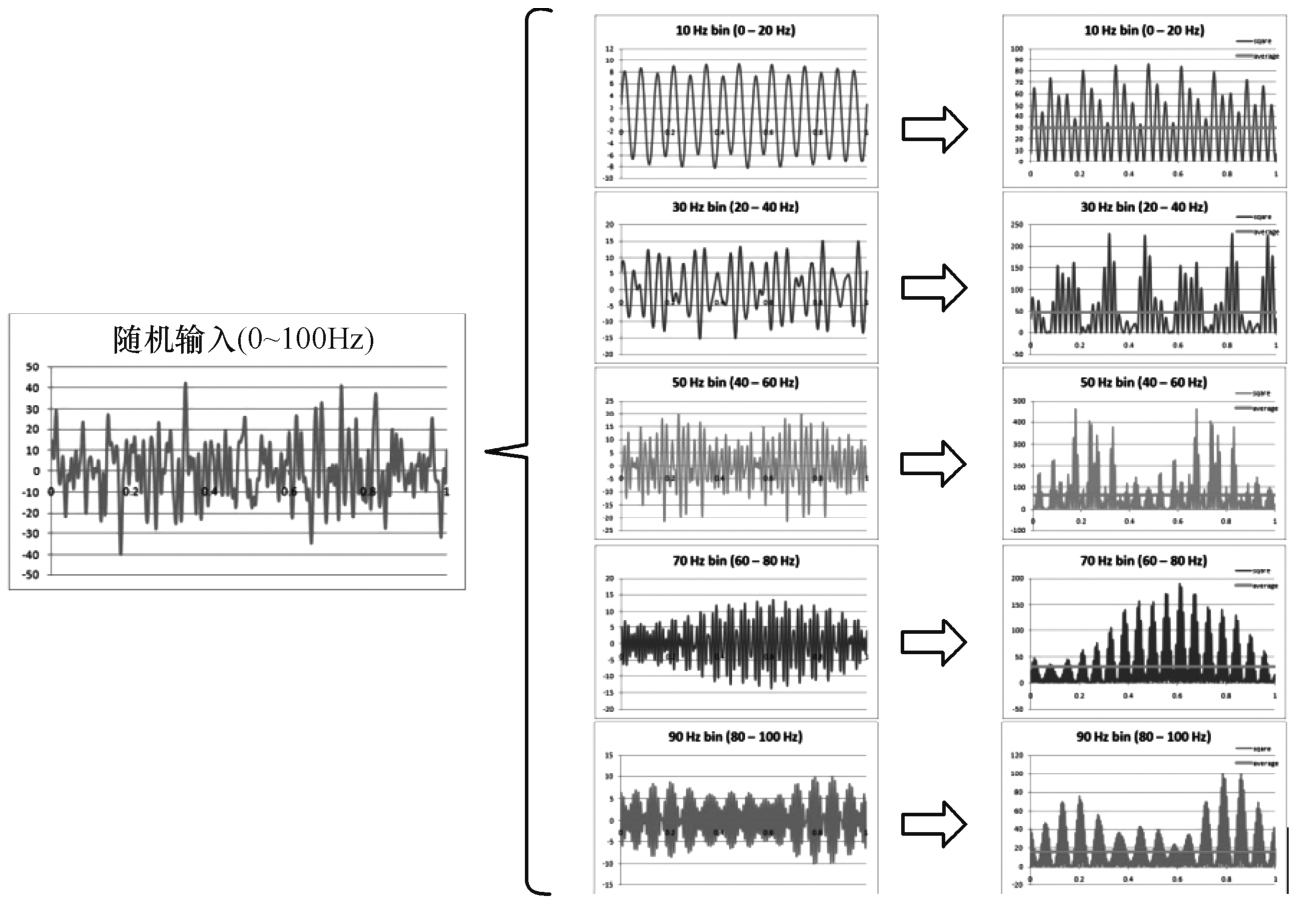
图1-3-1 总频率范围分解为子频率范围
在实际工程中,一般采用激励的方均值和频率带宽的比值来评估,即PSD=方均值/( f 1 -f 2 ),其单位是unit 2 /Hz。将值绘制成随子频率范围变化的曲线,然后在子频率范围内取中间值,最后在对数坐标系中绘制该曲线,如图1-3-2所示。
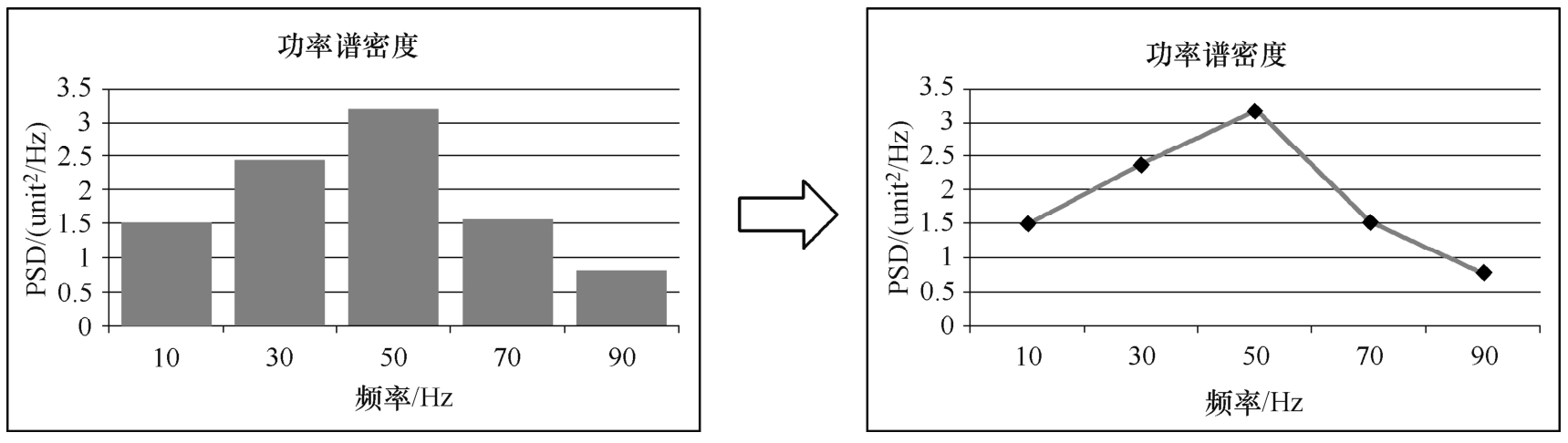
图1-3-2 PSD转化过程
ANSYS Mechanical功率谱密度可以采用多种形式,主要包括位移功率谱密度、速度功率谱密度、加速度功率谱密度和重力加速度功率谱密度等。位移功率谱密度、速度功率谱密度和加速度功率谱密度三者之间通过乘(除)频率2π f 的二次方能够较为容易地进行转换:
加速度功率谱密度与重力加速度功率谱密度也可以通过乘(除) g 2 进行相互转换:
ANSYS Mechanical随机振动分析分为单点随机振动分析和多点随机振动分析,随机振动分析过程中,PSD激励的施加位置在固定约束的位置点上,其中,多点随机振动分析需要在模型不同位置上施加不同的功率谱密度。
当输入随机振动PSD值并且用单自由度传递函数 H ( ω )和模态叠加分析技术,就可以求解得到PSD响应(RPSD)。在实际工程中,幅值和相位可以分别进行描述,也可以采用复数形式进行描述,这个描述的方法称为频率响应函数 H ( ω )(FRF):
其中,频响函数的幅值是输入与输出幅值的比值,计算公式如下:
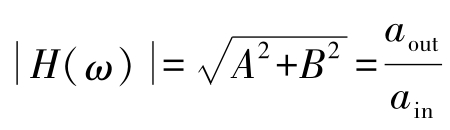
另外,频响函数虚部与实部的比值等于相位角的正切值,计算公式如下:
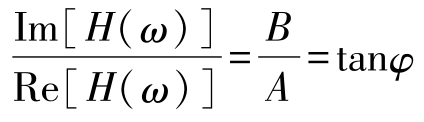
根据随机振动理论,对于单个输入的PSD值,系统输出为
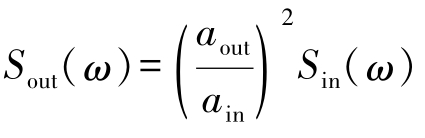
式中, S in ( ω )为谱密度输入(来自于输入的PSD曲线); S out ( ω )为谱密度响应; a in 为单自由度输入; a out 为计算的单自由度输出。
功率谱密度的响应RPSD计算通过输入的功率谱密度乘以传递函数进行表示,计算公式如下:
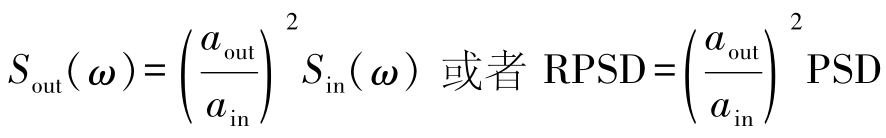
响应谱分析有6个步骤:建模、获得模态解、获得谱解、扩展模态、模态组合、观察结果。结构的振型和固有频率是谱分析所必需的数据,因此,要先进行模态分析。在扩展模态时,只需扩展到对最后进行的谱分析有影响的模态即可。