




 5.4 决策树的剪枝
5.4 决策树的剪枝
决策树生成算法递归地产生决策树,直到不能继续下去为止。这样产生的树往往对训练数据的分类很准确,但对未知的测试数据的分类却没有那么准确,即出现过拟合现象。过拟合的原因在于学习时过多地考虑如何提高对训练数据的正确分类,从而构建出过于复杂的决策树。解决这个问题的办法是考虑决策树的复杂度,对已生成的决策树进行简化。
在决策树学习中将已生成的树进行简化的过程称为剪枝(pruning)。具体地,剪枝从已生成的树上裁掉一些子树或叶结点,并将其根结点或父结点作为新的叶结点,从而简化分类树模型。
本节介绍一种简单的决策树学习的剪枝算法。
决策树的剪枝往往通过极小化决策树整体的损失函数(loss function)或代价函数(cost function)来实现。设树 T 的叶结点个数为| T |, t 是树 T 的叶结点,该叶结点有 N t 个样本点,其中 k 类的样本点有 N tk 个, k =1,2,…, K , H t ( T )为叶结点 t 上的经验熵, α ≥0为参数,则决策树学习的损失函数可以定义为
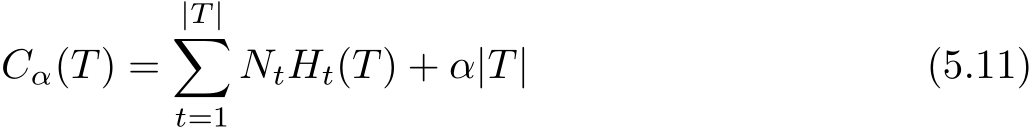
其中经验熵为
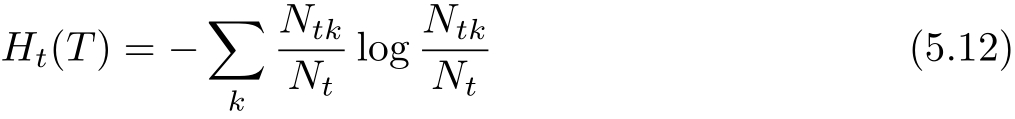
在损失函数中,将式(5.11)右端的第1项记作
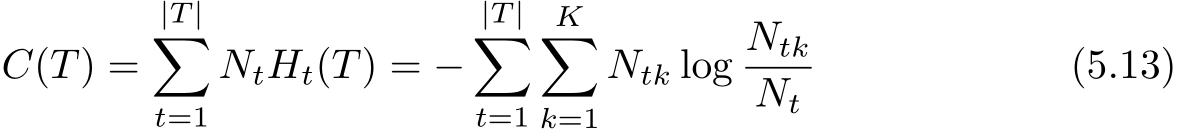
这时有

式(5.14)中, C ( T )表示模型对训练数据的预测误差,即模型与训练数据的拟合程度,| T |表示模型复杂度,参数 α ≥0控制两者之间的影响。较大的 α 促使选择较简单的模型(树),较小的 α 促使选择较复杂的模型(树)。 α =0意味着只考虑模型与训练数据的拟合程度,不考虑模型的复杂度。
剪枝,就是当 α 确定时,选择损失函数最小的模型,即损失函数最小的子树。当 α 值确定时,子树越大,往往与训练数据的拟合越好,但是模型的复杂度就越高;相反,子树越小,模型的复杂度就越低,但是往往与训练数据的拟合不好。损失函数正好表示了对两者的平衡。
可以看出,决策树生成只考虑了通过提高信息增益(或信息增益比)对训练数据进行更好的拟合。而决策树剪枝通过优化损失函数还考虑了减小模型复杂度。决策树生成学习局部的模型,而决策树剪枝学习整体的模型。
式(5.11)或式(5.14)定义的损失函数的极小化等价于正则化的极大似然估计。所以,利用损失函数最小原则进行剪枝就是用正则化的极大似然估计进行模型选择。
图5.6是决策树剪枝过程的示意图。下面介绍剪枝算法。
算法5.4(树的剪枝算法)
输入:生成算法产生的整个树 T ,参数 α ;
输出:修剪后的子树 T α 。
(1)计算每个结点的经验熵。
(2)递归地从树的叶结点向上回缩。
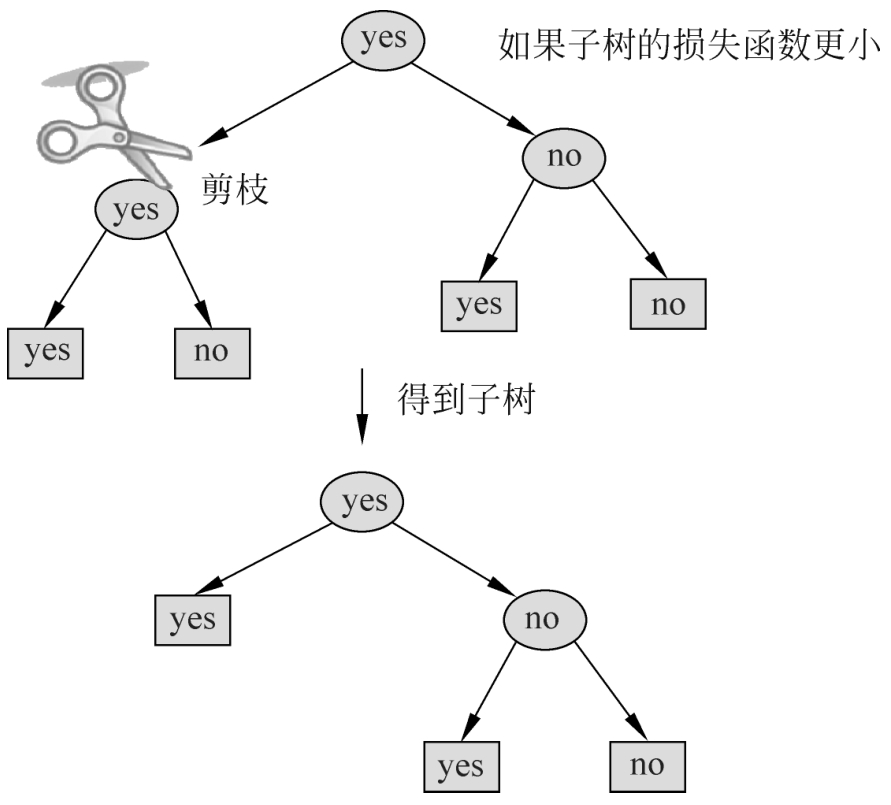
图5.6 决策树的剪枝
设一组叶结点回缩到其父结点之前与之后的整体树分别为 T B 与 T A ,其对应的损失函数值分别是 C α ( T B )与 C α ( T A ),如果

则进行剪枝,即将父结点变为新的叶结点。
(3)返回(2),直至不能继续为止,得到损失函数最小的子树 T α 。
注意,式(5.15)只需考虑两个树的损失函数的差,其计算可以在局部进行。所以,决策树的剪枝算法可以由一种动态规划的算法实现。类似的动态规划算法可参见文献[10]。