下载掌阅APP，畅读海量书库
立即打开
5.2 特征选择
特征选择在于选取对训练数据具有分类能力的特征。这样可以提高决策树学习的效率。如果利用一个特征进行分类的结果与随机分类的结果没有很大差别，则称这个特征是没有分类能力的。经验上扔掉这样的特征对决策树学习的精度影响不大。通常特征选择的准则是信息增益或信息增益比。
首先通过一个例子来说明特征选择问题。
例5.1
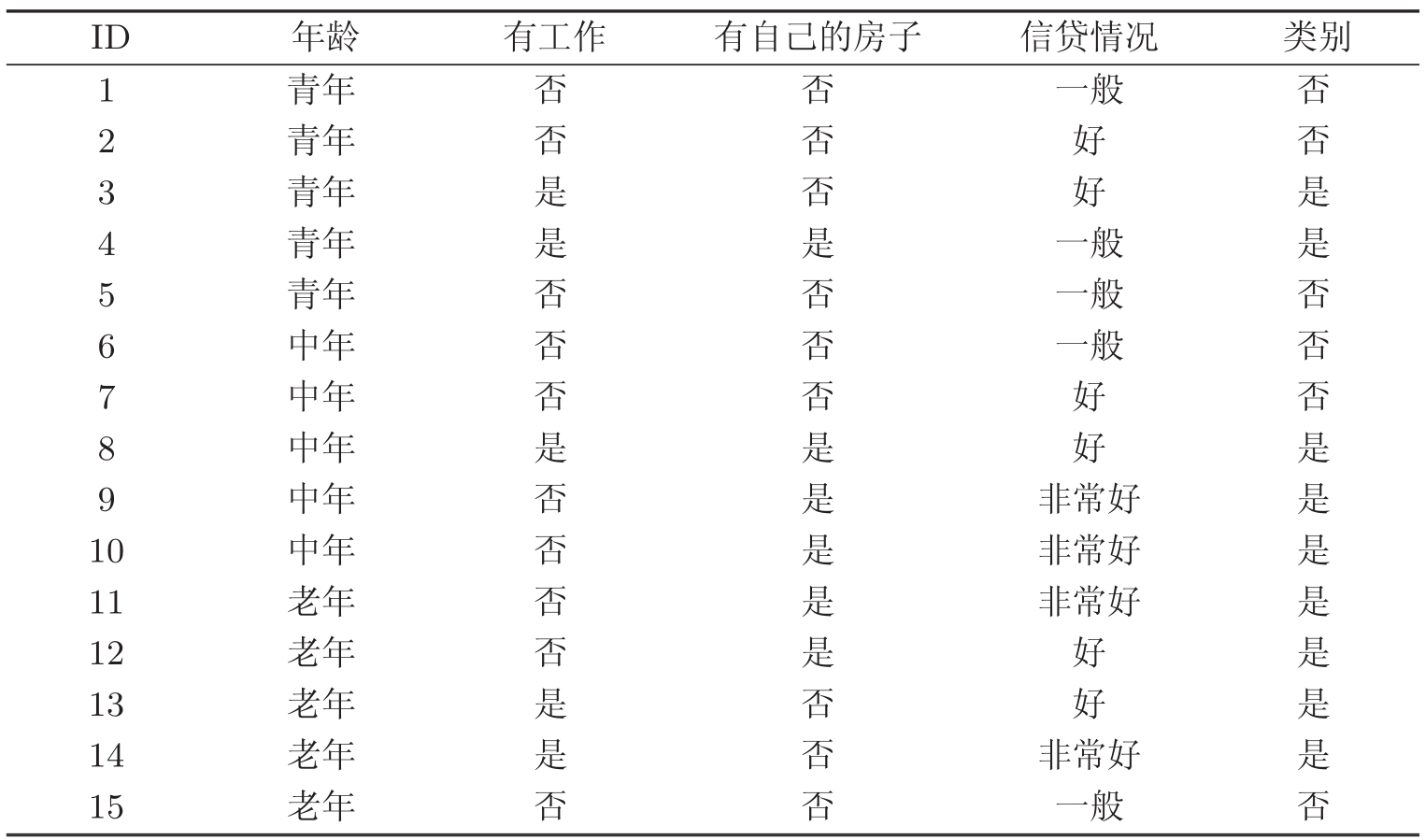
表5.1是一个由15个样本组成的贷款申请训练数据。数据包括贷款申请人的4个特征（属性）：第1个特征是年龄，有3个可能值：青年，中年，老年；第2个特征是有工作，有2个可能值：是，否；第3个特征是有自己的房子，有2个可能值：是，否；第4个特征是信贷情况，有3个可能值：非常好，好，一般。表的最后一列是类别，是否同意贷款，取2个值：是，否。
表5.1 贷款申请样本数据表
希望通过所给的训练数据学习一个贷款申请的决策树，用以对未来的贷款申请进行分类，即当新的客户提出贷款申请时，根据申请人的特征利用决策树决定是否批准贷款申请。
特征选择是决定用哪个特征来划分特征空间。
图5.3表示从表5.1数据学习到的两个可能的决策树，分别由两个不同特征的根结点构成。图5.3（a）所示的根结点的特征是年龄，有3个取值，对应于不同的取值有不同的子结点。图5.3（b）所示的根结点的特征是有工作，有2个取值，对应于不同的取值有不同的子结点。两个决策树都可以从此延续下去。问题是：究竟选择哪个特征更好些？这就要求确定选择特征的准则。直观上，如果一个特征具有更好的分类能力，或者说，按照这一特征将训练数据集分割成子集，使得各个子集在当前条件下有最好的分类，那么就更应该选择这个特征。信息增益（information gain）就能够很好地表示这一直观的准则。
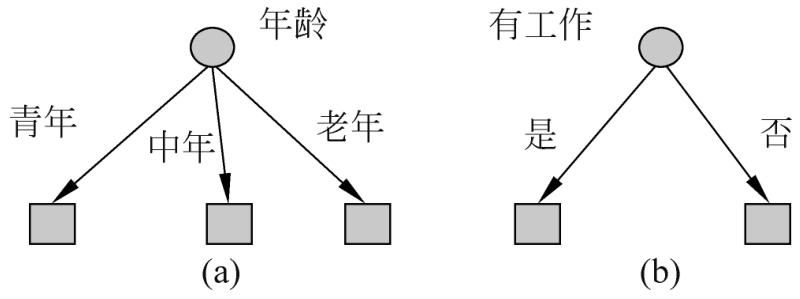
图5.3 不同特征决定的不同决策树
为了便于说明，先给出熵与条件熵的定义。
在信息论与概率统计中，熵（entropy）是表示随机变量不确定性的度量。设 X 是一个取有限个值的离散随机变量，其概率分布为
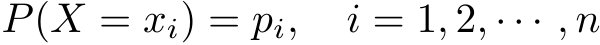
则随机变量 X 的熵定义为
在式（5.1）中，若 p i =0，则定义0log0=0。通常，式（5.1）中的对数以2为底或以e为底（自然对数），这时熵的单位分别称作比特（bit）或纳特（nat）。由定义可知，熵只依赖于 X 的分布，而与 X 的取值无关，所以也可将 X 的熵记作 H （ p ），即
熵越大，随机变量的不确定性就越大。从定义可验证
当随机变量只取两个值，例如1，0时，即 X 的分布为
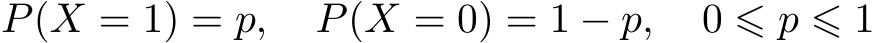
熵为
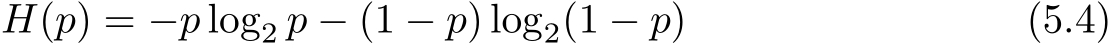
这时，熵 H （ p ）随概率 p 变化的曲线如图5.4所示（单位为比特）。
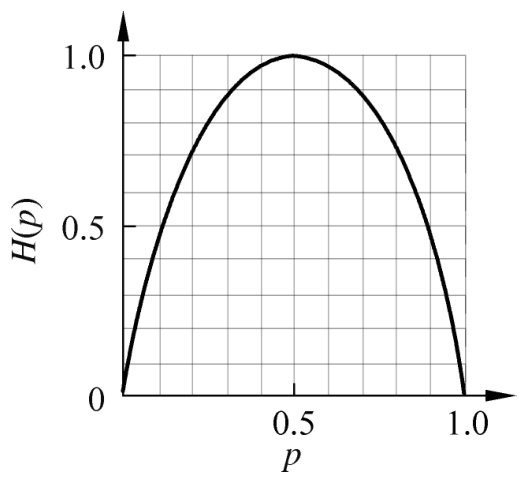
图5.4 分布为伯努利分布时熵与概率的关系
当 p =0或 p =1时 H （ p ）=0，随机变量完全没有不确定性。当 p =0.5时， H （ p ）=1，熵取值最大，随机变量不确定性最大。
设有随机变量（ X , Y ），其联合概率分布为
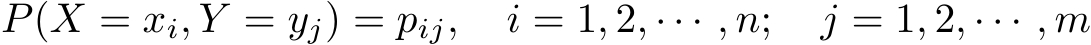
条件熵 H （ Y | X ）表示在已知随机变量 X 的条件下随机变量 Y 的不确定性。随机变量 X 给定的条件下随机变量 Y 的条件熵（conditional entropy） H （ Y | X ），定义为 X 给定条件下 Y 的条件概率分布的熵对 X 的数学期望
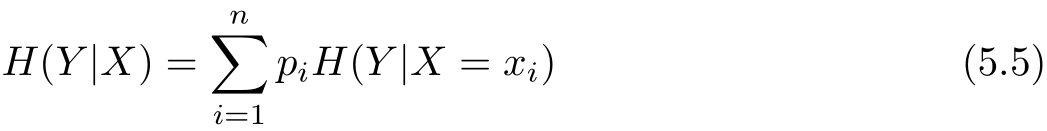
这里， p i = P （ X = x i ）， i =1,2,…, n 。
当熵和条件熵中的概率由数据估计（特别是极大似然估计）得到时，所对应的熵与条件熵分别称为经验熵（empirical entropy）和经验条件熵（empirical conditional entropy）。此时，如果有0概率，令0log0=0。
信息增益（information gain）表示得知特征 X 的信息而使得类 Y 的信息的不确定性减少的程度。
定义5.2（信息增益） 特征 A 对训练数据集 D 的信息增益 g （ D , A ），定义为集合 D 的经验熵 H （ D ）与特征 A 给定条件下 D 的经验条件熵 H （ D | A ）之差，即
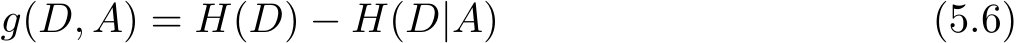
一般地，熵 H （ Y ）与条件熵 H （ Y | X ）之差称为互信息（mutual information）。决策树学习中的信息增益等价于训练数据集中类与特征的互信息。
决策树学习应用信息增益准则选择特征。给定训练数据集 D 和特征 A ，经验熵 H （ D ）表示对数据集 D 进行分类的不确定性。而经验条件熵 H （ D | A ）表示在特征 A 给定的条件下对数据集 D 进行分类的不确定性。那么它们的差，即信息增益，就表示由于特征 A 而使得对数据集 D 的分类的不确定性减少的程度。显然，对于数据集 D 而言，信息增益依赖于特征，不同的特征往往具有不同的信息增益。信息增益大的特征具有更强的分类能力。
根据信息增益准则的特征选择方法是：对训练数据集（或子集） D ，计算其每个特征的信息增益，并比较它们的大小，选择信息增益最大的特征。
设训练数据集为
D
，|
D
|表示其样本容量，即样本个数。设有
K
个类
C
k
，
k
=
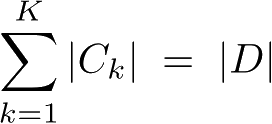1,2,…,
K
，|
C
k
|为属于类
C
k
的样本个数。设特征
A
有
n
个不同的取值{
a
1
,
a
2
,…,
a
n
}
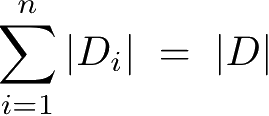，根据特征
A
的取值将
D
划分为
n
个子集
D
1
,
D
2
,…,
D
n
，|
D
i
|为
D
i
的样本个数。记子集
D
i
中属于类
C
k
的样本的集合为
D
ik
，即
D
ik
=
D
i
∩
C
k
，|
D
ik
|为
D
ik
的样本个数。于是信息增益的算法如下。
算法5.1（信息增益的算法）
输入：训练数据集 D 和特征 A ；
输出：特征 A 对训练数据集 D 的信息增益 g （ D , A ）。
（1）计算数据集 D 的经验熵 H （ D ）
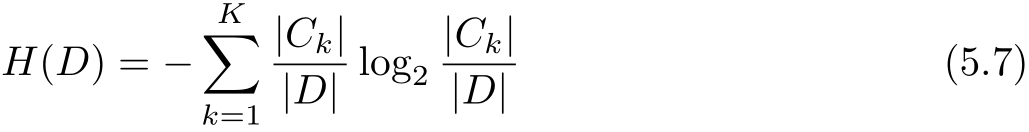
（2）计算特征 A 对数据集 D 的经验条件熵 H （ D | A ）
（3）计算信息增益
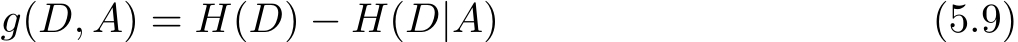
例5.2 对表5.1所给的训练数据集 D ，根据信息增益准则选择最优特征。
解 首先计算经验熵 H （ D ）。
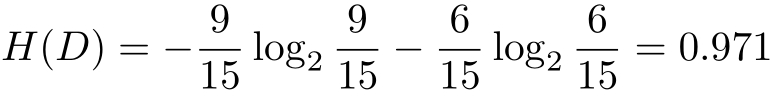
然后计算各特征对数据集 D 的信息增益。分别以 A 1 ， A 2 ， A 3 ， A 4 表示年龄、有工作、有自己的房子和信贷情况4个特征，则
（1）
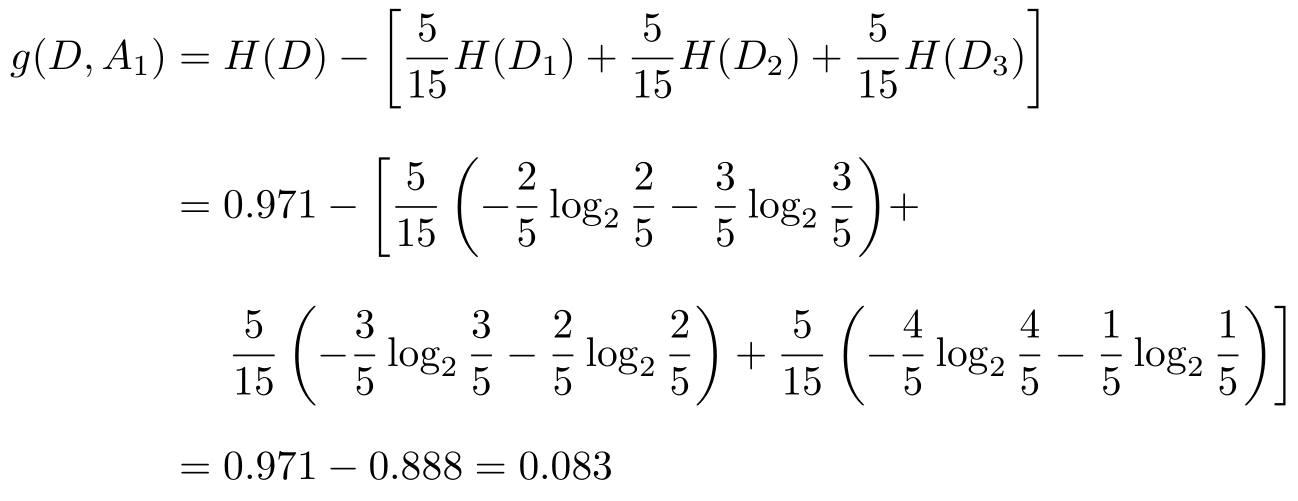
这里 D 1 ， D 2 ， D 3 分别是 D 中 A 1 （年龄）取值为青年、中年和老年的样本子集。类似地，
（2）
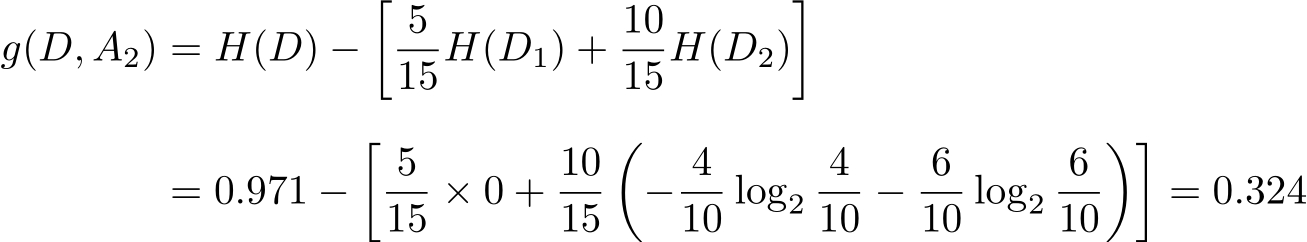
（3）
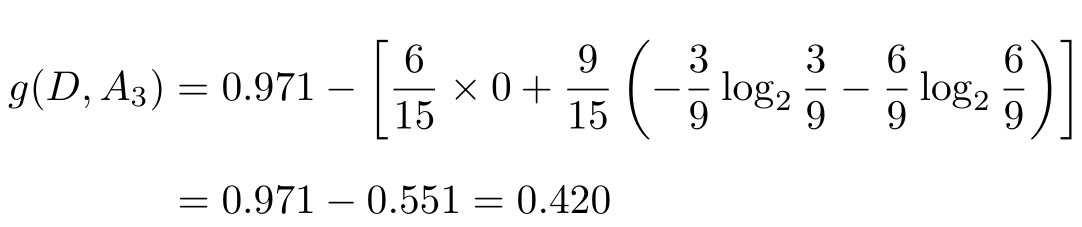
（4）
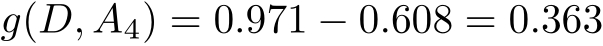
最后，比较各特征的信息增益值。由于特征 A 3 （有自己的房子）的信息增益值最大，所以选择特征 A 3 作为最优特征。
以信息增益作为划分训练数据集的特征，存在偏向于选择取值较多的特征的问题。使用信息增益比（information gain ratio）可以对这一问题进行校正。这是特征选择的另一准则。
定义5.3（信息增益比） 特征 A 对训练数据集 D 的信息增益比 g R （ D , A ）定义为其信息增益 g （ D , A ）与训练数据集 D 关于特征 A 的值的熵 H A （ D ）之比，即
其中，
，
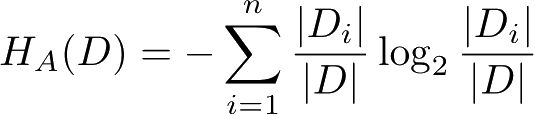n
是特征
A
取值的个数。