2.2　感知机学习策略

2.2.1　数据集的线性可分性

定义2.2（数据集的线性可分性） 给定一个数据集

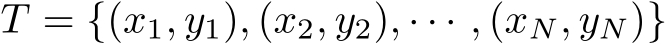
其中， x _i ∈ X = R ⁿ ， y _i ∈ Y ={+1,−1}， i =1,2,…, N ，如果存在某个超平面 S

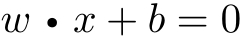
能够将数据集的正实例点和负实例点完全正确地划分到超平面的两侧，即对所有 y _i =+1的实例 i ，有 w · x _i + b >0，对所有 y _i =−1的实例 i ，有 w · x _i + b <0，则称数据集 T 为线性可分数据集（linearly separable data set）；否则，称数据集 T 线性不可分。

2.2.2　感知机学习策略

假设训练数据集是线性可分的，感知机学习的目标是求得一个能够将训练集正实例点和负实例点完全正确分开的分离超平面。为了找出这样的超平面，即确定感知机模型参数 w ， b ，需要确定一个学习策略，即定义（经验）损失函数并将损失函数极小化。

损失函数的一个自然选择是误分类点的总数。但是，这样的损失函数不是参数 w ， b 的连续可导函数，不易优化。损失函数的另一个选择是误分类点到超平面 S 的总距离，这是感知机所采用的。为此，首先写出输入空间 R ⁿ 中任一点 x ₀ 到超平面 S 的距离：

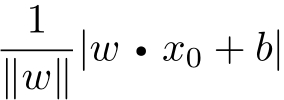
这里，‖ w ‖是 w 的 L ₂ 范数。

其次，对于误分类的数据（ x _i , y _i ）来说，

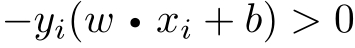
成立。因为当 w · x _i + b >0时， y _i =−1；而当 w · x _i + b <0时， y _i =+1。因此，误分类点 x _i 到超平面 S 的距离是

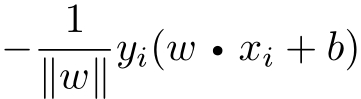
这样，假设超平面 S 的误分类点集合为 M ，那么所有误分类点到超平面 S 的总距离为

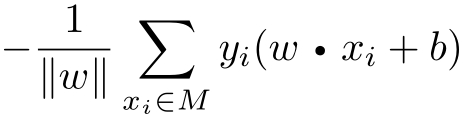
不考虑 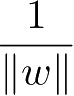，就得到感知机学习的损失函数 ^[1] 。

给定训练数据集

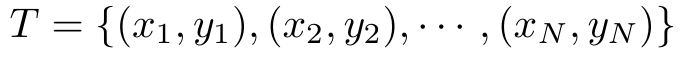
其中， x _i ∈ X = R ⁿ ， y _i ∈ Y ={+1,−1}， i =1,2,…, N 。感知机sign（ w · x + b ）学习的损失函数定义为

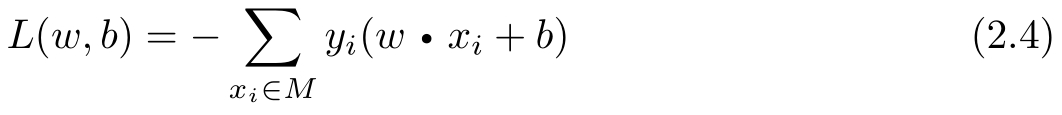
其中 M 为误分类点的集合。这个损失函数就是感知机学习的经验风险函数。

显然，损失函数 L （ w , b ）是非负的。如果没有误分类点，损失函数值是0。而且，误分类点越少，误分类点离超平面越近，损失函数值就越小。一个特定的样本点的损失函数：在误分类时是参数 w ， b 的线性函数，在正确分类时是0。因此，给定训练数据集 T ，损失函数 L （ w , b ）是 w ， b 的连续可导函数。

感知机学习的策略是在假设空间中选取使损失函数式（2.4）最小的模型参数 w , b ,即感知机模型。 NS2gasoQl37HLtJa5Mv8Vv8yGLXfn6YjURu0LOFMfjVPVnr0oMC+akJax0jhlyF6