下载掌阅APP，畅读海量书库
立即打开
1.6 泛化能力
学习方法的泛化能力（generalization ability）是指由该方法学习到的模型对未知数据的预测能力，是学习方法本质上重要的性质。现实中采用最多的办法是通过测试误差来评价学习方法的泛化能力。但这种评价是依赖于测试数据集的。因为测试数据集是有限的，很有可能由此得到的评价结果是不可靠的。统计学习理论试图从理论上对学习方法的泛化能力进行分析。
首先给出泛化误差的定义。如果学到的模型是
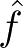，那么用这个模型对未知数据预测的误差即为泛化误差（generalization error）：
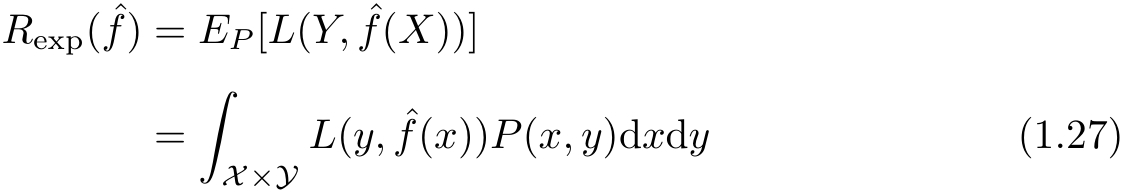
泛化误差反映了学习方法的泛化能力，如果一种方法学习的模型比另一种方法学习的模型具有更小的泛化误差，那么这种方法就更有效。事实上，泛化误差就是所学习到的模型的期望风险。
学习方法的泛化能力分析往往是通过研究泛化误差的概率上界进行的，简称为泛化误差上界（generalization error bound）。具体来说，就是通过比较两种学习方法的泛化误差上界的大小来比较它们的优劣。泛化误差上界通常具有以下性质：它是样本容量的函数，当样本容量增加时，泛化上界趋于0；它是假设空间容量（capacity）的函数，假设空间容量越大，模型就越难学，泛化误差上界就越大。
下面给出一个简单的泛化误差上界的例子：二类分类问题的泛化误差上界。
考虑二类分类问题。已知训练数据集 T ={（ x 1 , y 1 ）,（ x 2 , y 2 ）,…,（ x N , y N ）}， N 是样本容量， T 是从联合概率分布 P （ X , Y ）独立同分布产生的， X ∈ R n ， Y ∈{−1,+1}。假设空间是函数的有限集合 F ={ f 1 , f 2 ,…, f d }， d 是函数个数。设 f 是从 F 中选取的函数。损失函数是0-1损失。关于 f 的期望风险和经验风险分别是
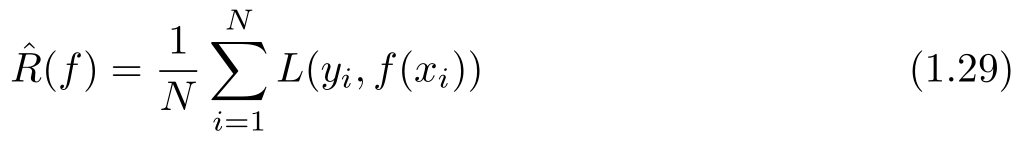
经验风险最小化函数是
f N 依赖训练数据集的样本容量 N 。人们更关心的是 f N 的泛化能力
下面讨论从有限集合 F ={ f 1 , f 2 ,…, f d }中任意选出的函数 f 的泛化误差上界。
定理1.1（泛化误差上界） 对二类分类问题，当假设空间是有限个函数的集合 F ={ f 1 , f 2 ,…, f d }时，对任意一个函数 f ∈ F ，至少以概率1− δ ，0< δ <1，以下不等式成立：
其中，
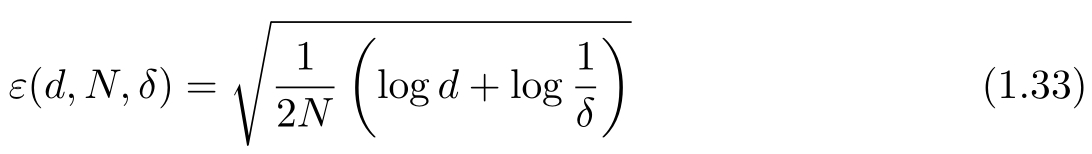
不等式（1.32）左端
R
（
f
）是泛化误差，右端即为泛化误差上界。在泛化误差上界中，第1项是训练误差，训练误差越小，泛化误差也越小。第2项
ε
（
d,N,δ
）是
N
的单调递减函数，当
N
趋于无穷时趋于0；同时它也是
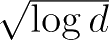阶的函数，假设空间
F
包含的函数越多，其值越大。
证明 在证明中要用到Hoeffding不等式，先叙述如下。
设
X
1
,
X
2
,…,
X
N
是独立随机变量，且
X
i
∈[
a
i
,
b
i
]，
i
=1,2,…,
N
；
是
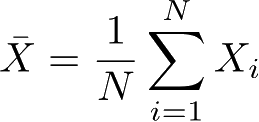X
1
,
X
2
,…,
X
N
的经验均值，即，则对任意
t
>0，以下不等式成立：
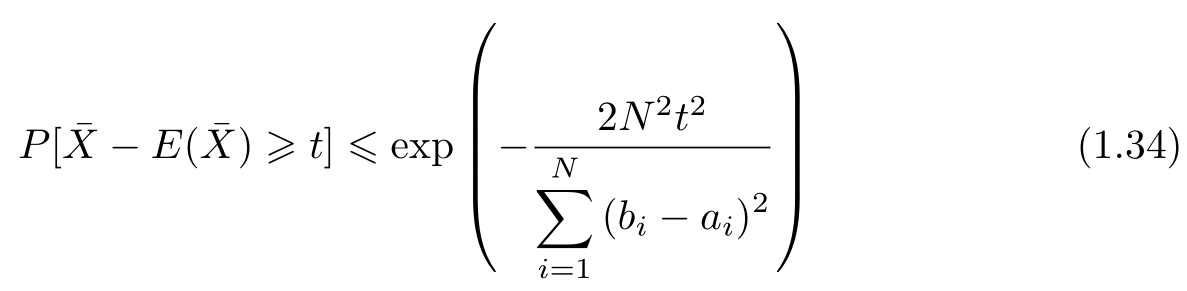
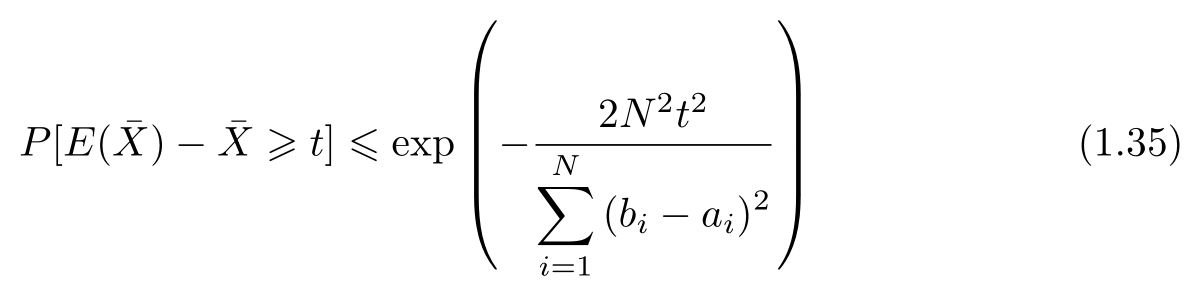
Hoeffding不等式的证明省略了，这里用来推导泛化误差上界。
对任意函数
f
∈
F
，
是
N
个独立的随机变量
L
（
Y
,
f
（
X
））的样本均值，
R
（
f
）是随机变量
L
（
Y
,
f
（
X
））的期望值。如果损失函数取值于区间[0,1]，即对所有
i
，[
a
i
,
b
i
]=[0,1]，那么由Hoeffding不等式（1.35）不难得知，对
ε
>0，以下不等式成立：
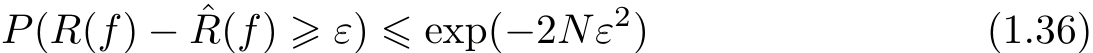
由于 F ={ f 1 , f 2 ,…, f d }是一个有限集合，故
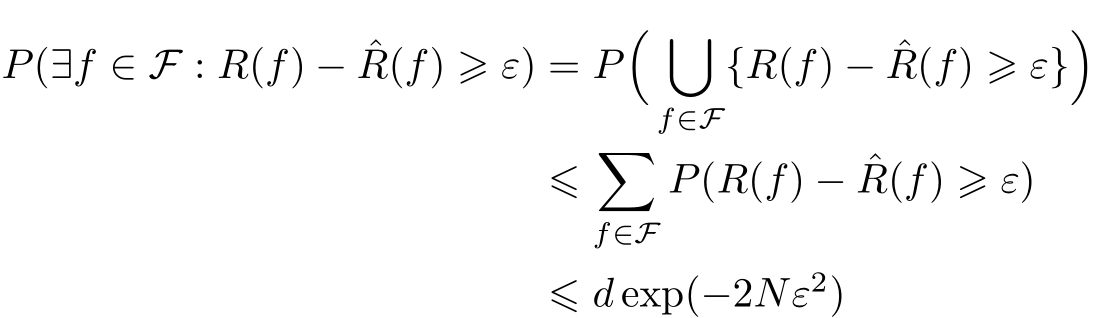
或者等价的，对任意 f ∈ F ，有
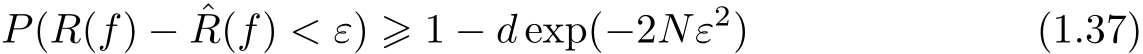
令
则
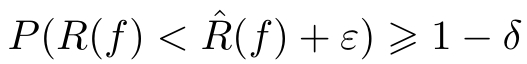
即至少以概率1−
δ
有
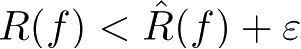，其中ε由式（1.38）得到，即为式（1.33）。
从泛化误差上界可知，
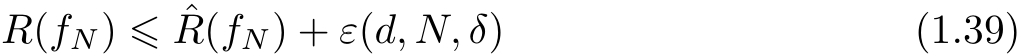
其中， ε （ d,N,δ ）由式（1.33）定义， f N 由式（1.30）定义。
以上讨论的只是假设空间包含有限个函数情况下的泛化误差上界，对一般的假设空间要找到泛化误差界就没有这么简单，这里不作介绍。