





移动平均 (Moving Average, MA)又称 滑动平均 、 滚动平均 (running average, rolling average),是一个统计学的概念,是指通过创建总体数据中一系列子集的平均数来对总体数据进行分析的一种技术手段。移动平均可以分为简单移动平均、累积移动平均和加权移动平均等。
简单移动平均 (Simple Moving Average, SMA)是指周期性计算某确定数量数据的平均值,如图1-11所示。

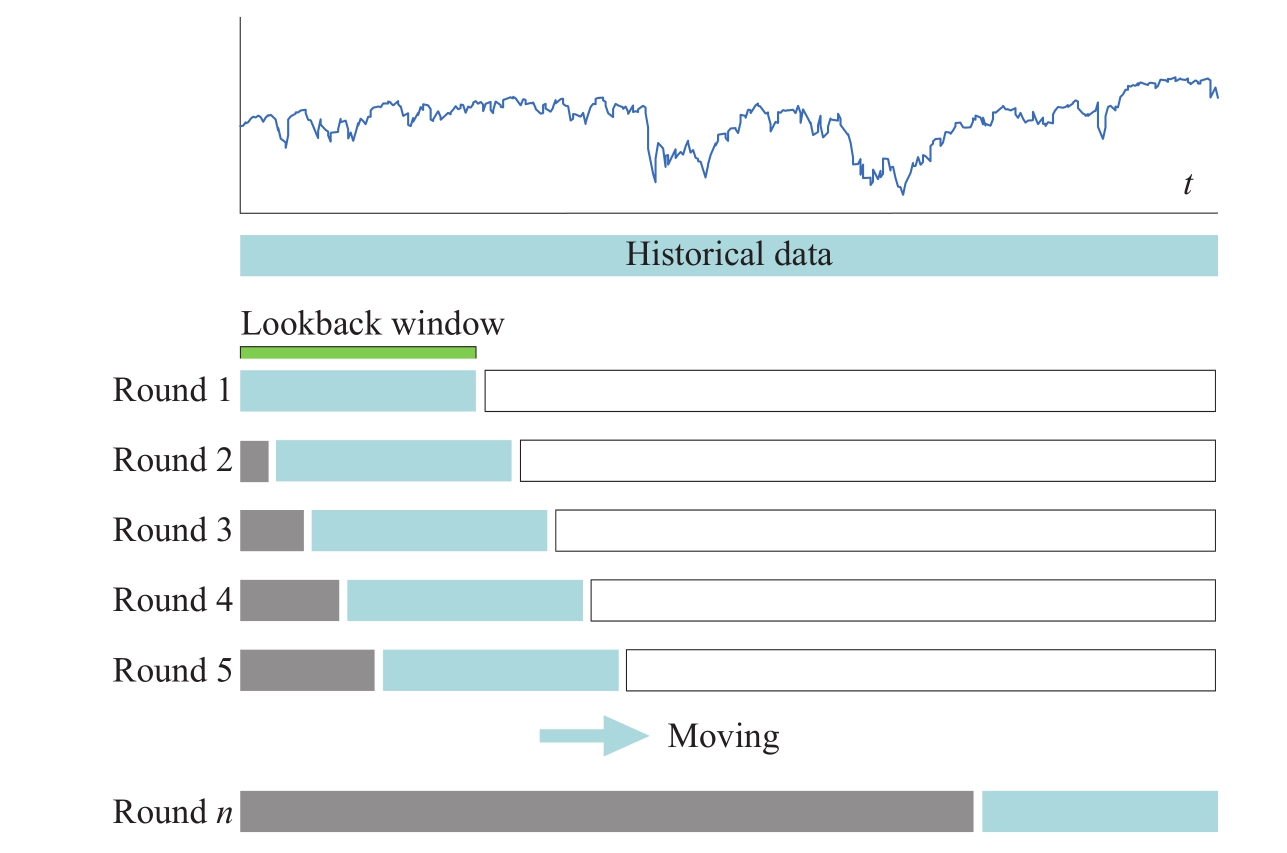
图1-11 简单移动平均
在每次计算时,剔除最老的数据,加入最新的数据,形成一个新的子数据,再进行取平均计算。但是,没有必要对整个子数据集进行求和再取平均的计算,可以直接借助上一步已经得到的均值,简化的计算公式为:

Pandas运算包提供了一种非常简单的方法来计算简单移动平均波动率,即通过rolling().std()函数计算某 移动窗口 (rolling window)的标准差,下面的代码利用获取的标普指数10年的历史数据,分别以5天、50天、100天和250天为移动窗口,绘制相应的历史波动率的曲线。

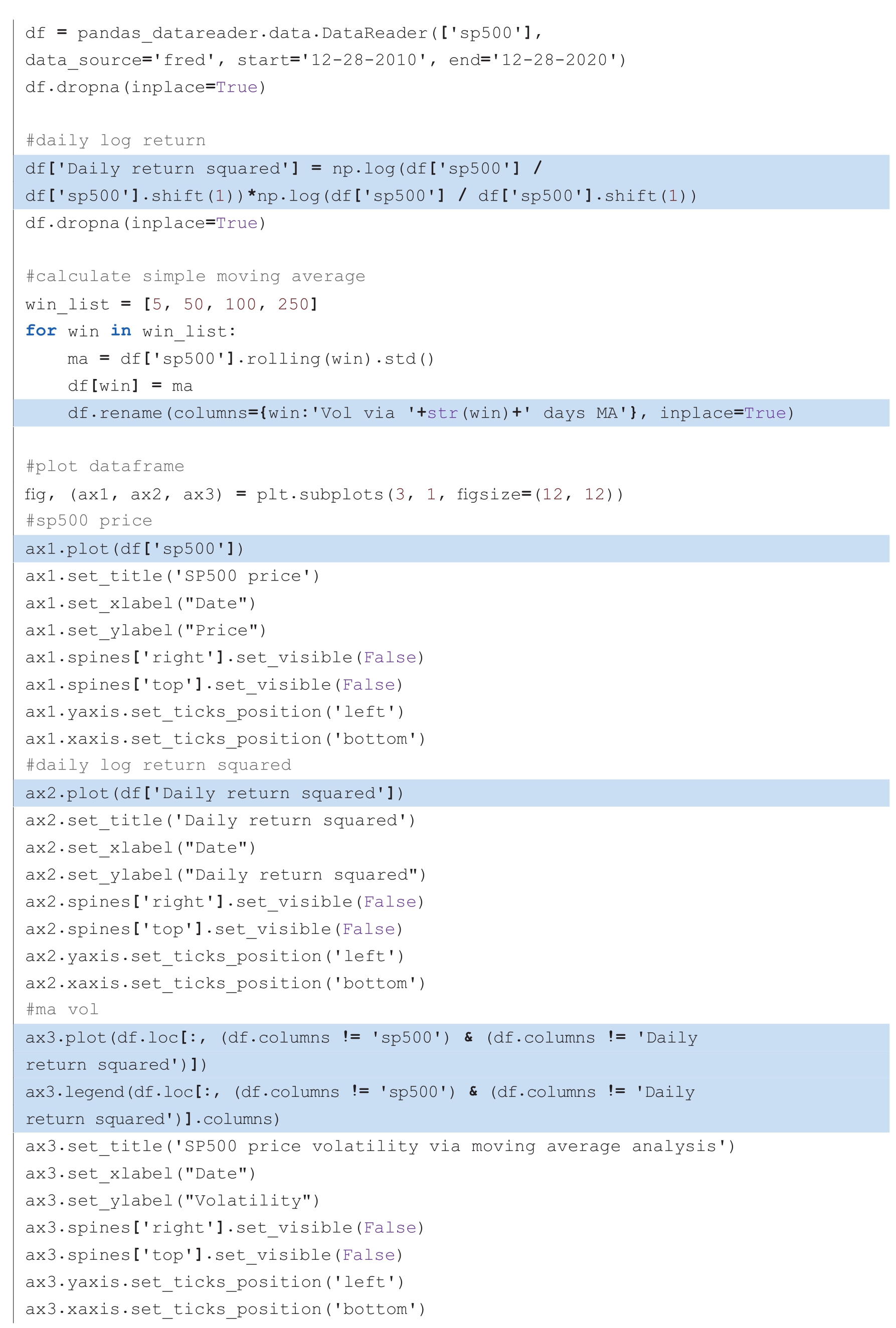

如图1-12所示,简单移动平均使得数据曲线更加平滑,便于从冗杂的数据中整理出较为清晰的脉络,以此可以帮助分析隐含于数据中的真正趋势。随着移动窗口的变大,数据曲线会变得更简单平滑,但是需要注意,数据的细节在这个过程中会丢失,因此需要根据具体情况,合理地选择移动窗口的大小。
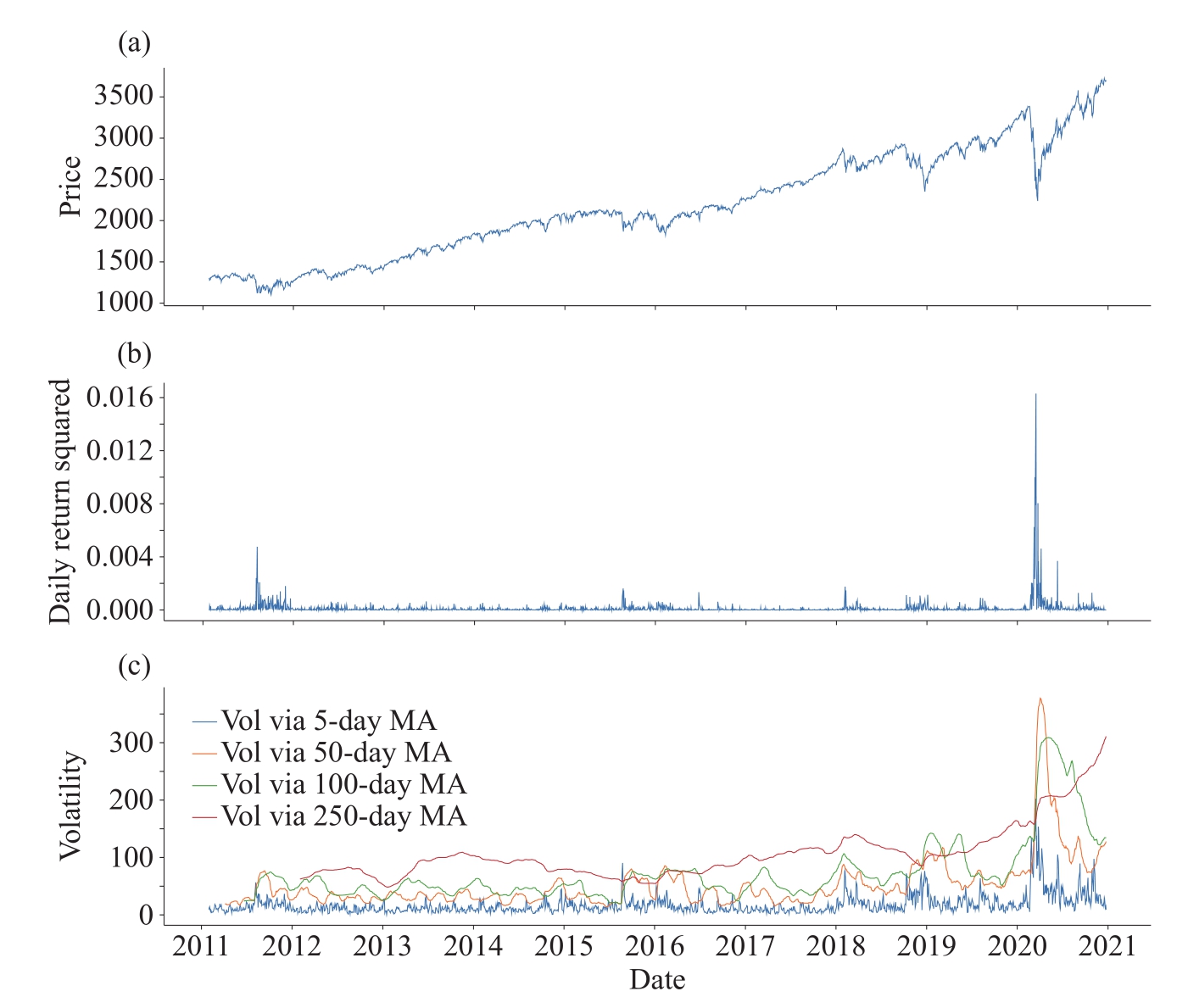
图1-12 简单移动平均计算波动率
与简单移动平均类似, 累积移动平均 (Cumulative Moving Average, CMA)也是周期性计算一系列数据的平均值,公式为:
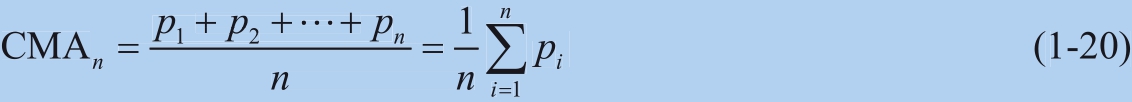
但是,不同于简单移动平均,移除旧的数据,加入新的数据,累积移动平均会考虑所有的数据。具体地说,累积移动平均通过有序加入新的数据,并对该数据与原来所有数据进行平均,得到平均值,直到当前数据点为止,如图1-13所示。
同样,类似于简单移动平均,在每次计算中,没有必要计算所有数据的总和,然后除以数据个数,得到平均值。累积移动平均在得到新的数据后,可以简单地更新累积平均值,用式(1-21)来简化计算。

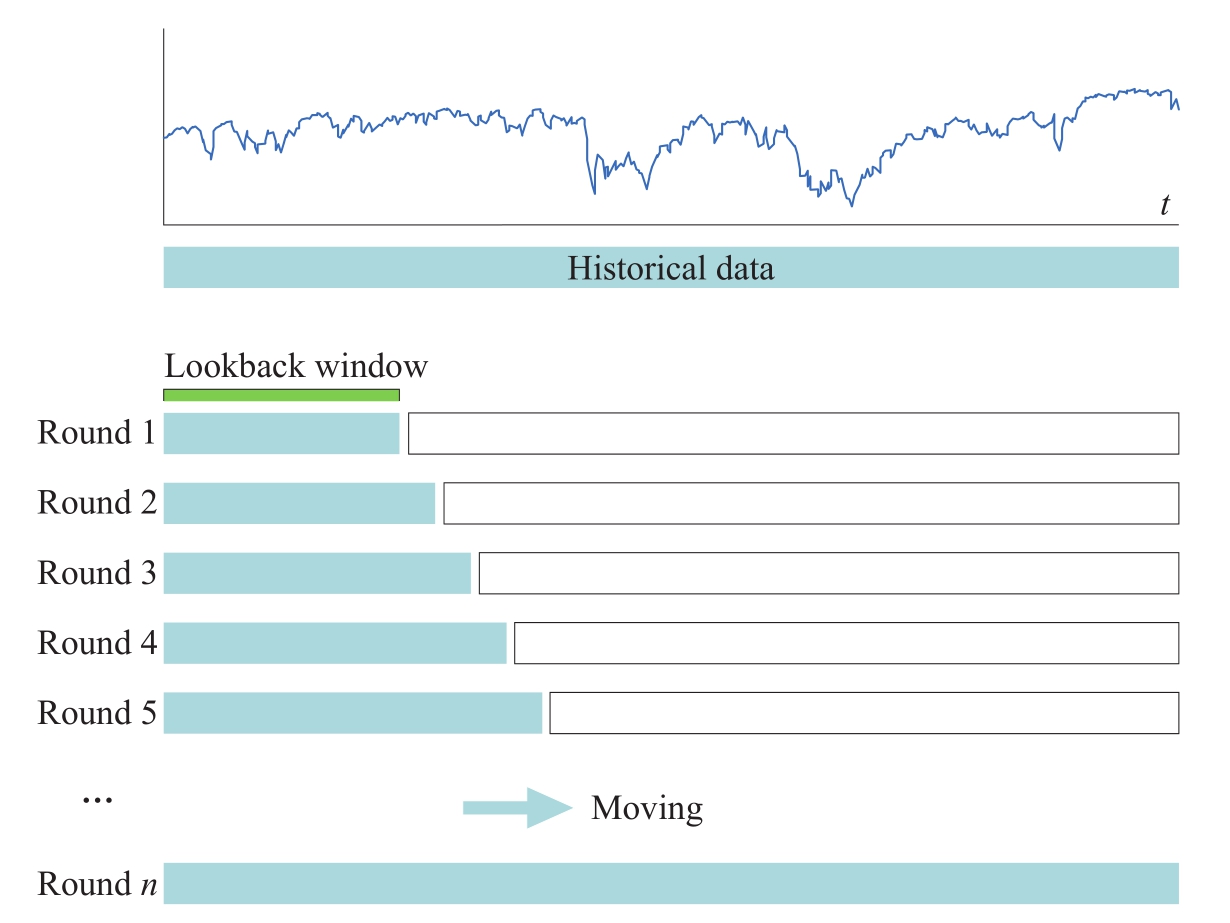
图1-13 累积移动平均方法示意图
前面介绍过的简单移动平均,可以利用rolling()函数进行计算。对于累积移动平均,Pandas运算包也提供了一个函数—expanding().std()来计算累积移动标准差,rolling()函数移动窗口的大小会被预先设定,因此是固定的,而expanding()函数移动窗口是不断变化的,即每次移动窗口会加1,也正因如此,该函数名被称为“ 扩展 ”(expanding)。
下面的代码利用获取的标普指数10年的历史数据,通过expanding().std()函数计算累积波动率,并绘制曲线。
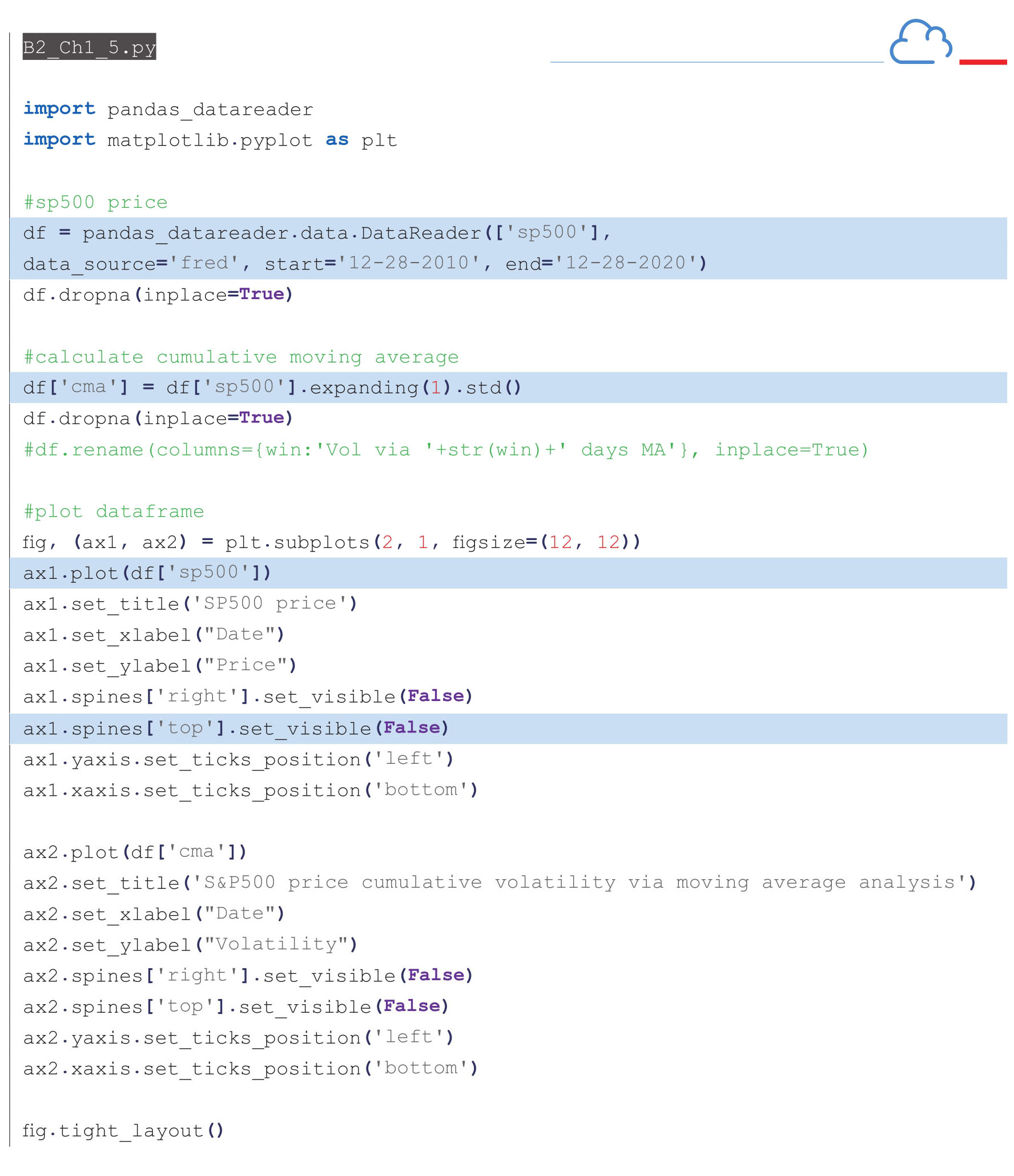
累积移动平均是考虑所有数据的叠加,如图1-14所示,它对于累积的数据曲线具有平滑的作用,但是,与简单移动平均不同,它并不能很好地反映整个数据的走势。
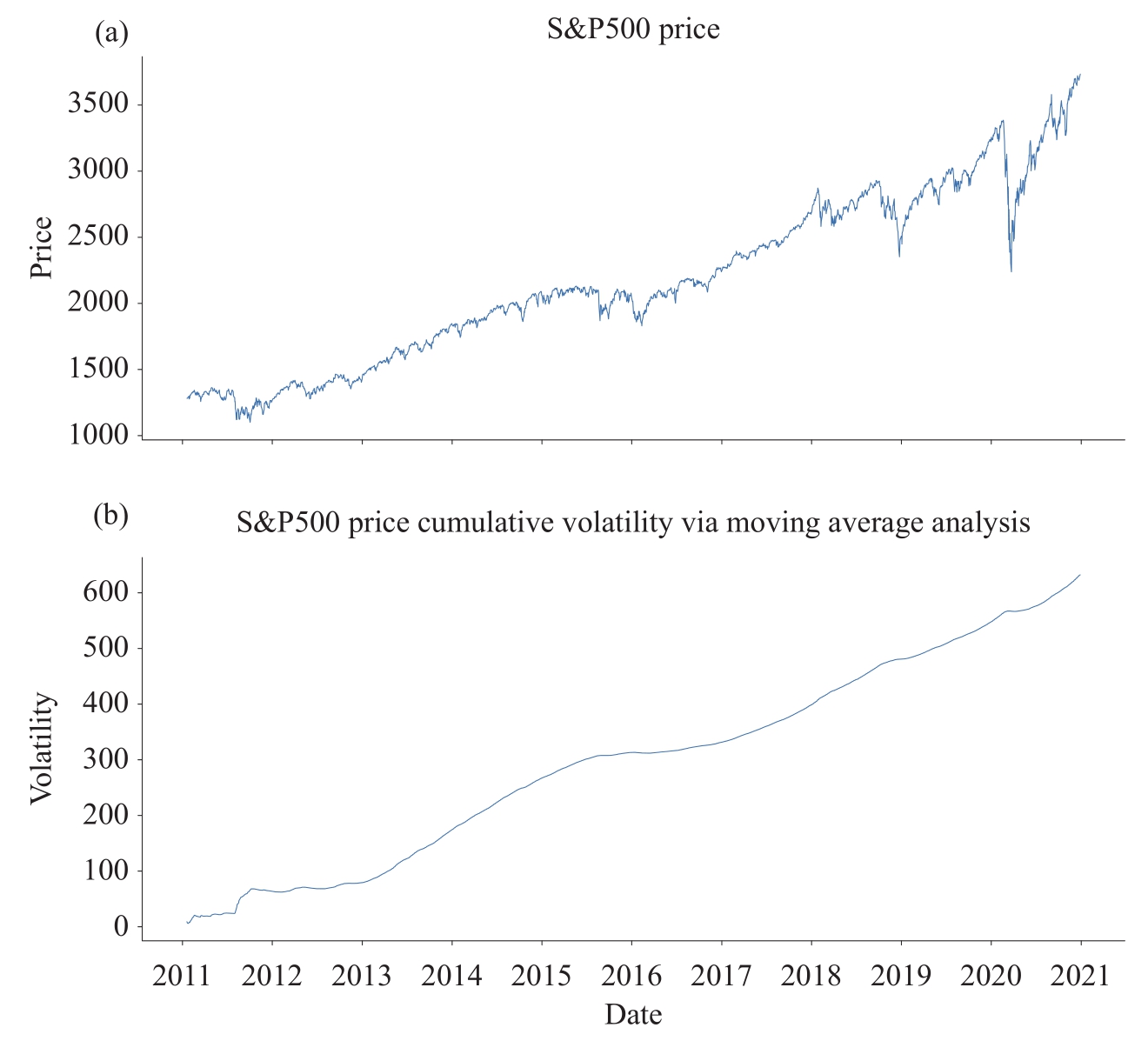
图1-14 累积移动平均波动率
前面介绍的,无论是简单移动平均还是累积移动平均,对于所有数据,无论距离当前时刻的远近,它们的权重是相同的,但是在实际应用中,近期的数据往往对当前数据有相对较大的影响,也更能反映当前以及未来的趋势。基于以上的认知,出现了 加权移动平均法 (weighted moving average),它是根据数据的时间序列,赋予不同的权重,再依照权重求得移动平均值。如前所述,采用加权移动平均法,近期值对预测值有较大影响,它更能反映近期变化的趋势。如图1-15所示对比了未加权与加权移动平均的不同。
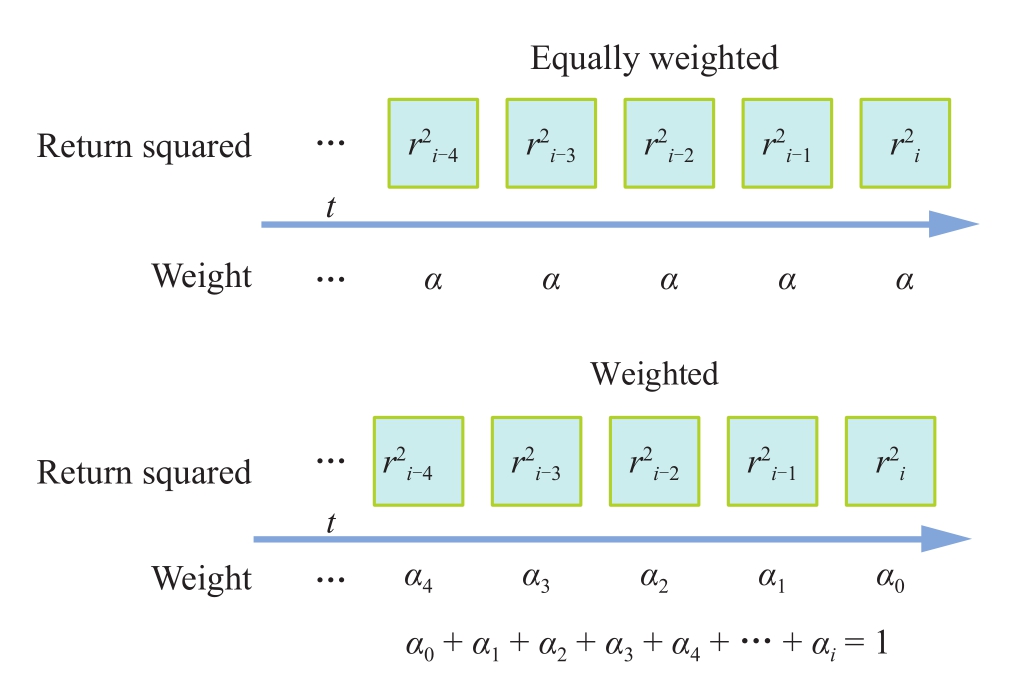
图1-15 未加权与加权移动平均对照图
指数移动加权平均 (Exponentially Weighted Moving Average, EWMA)是常用的一种加权平均方法,是指各数值的加权系数随时间呈指数式递减,越靠近当前时刻的数值加权系数就越大。如图1-16所示为指数加权移动平均的权重以指数形式的变化。
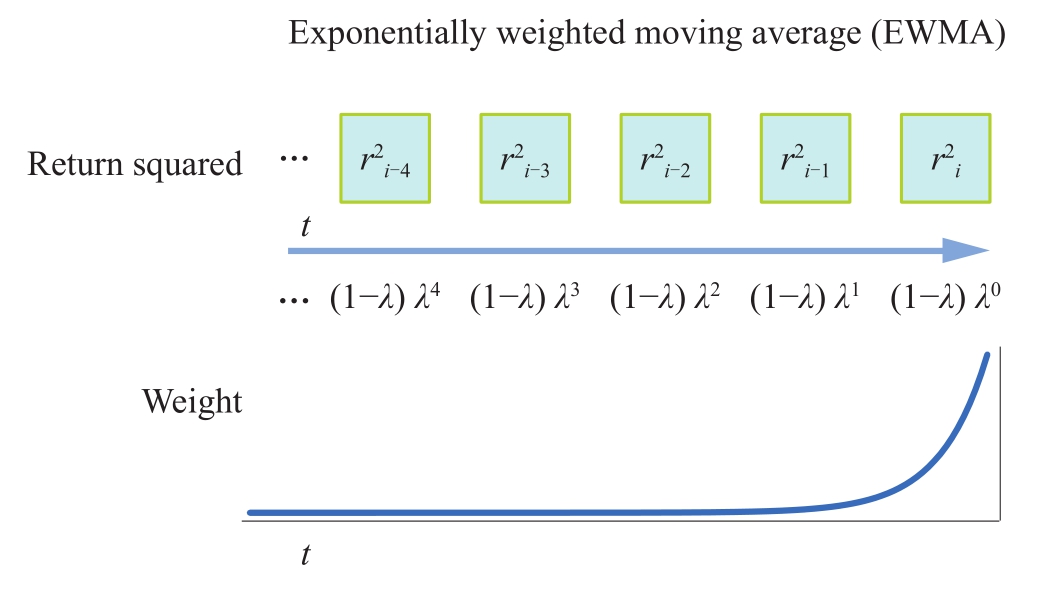
图1-16 指数加权移动平均示意图
指数加权移动平均在波动率上的应用最初是由RiskMetrics于1996年首次提出的。理论上,这种方法需要计算如图1-16所示一系列权重的序列,但是在实际应用上,通常会用到式(1-22)。

其中: λ 为 衰减因子 (decay factor); σ n 是当前时刻的波动率; σ n -1 是上一时刻的波动率; r n -1 是上一时刻的回报率。
为了方便大家理解,通过下面的例子进行简单推导,讨论衰减因子如何影响波动率计算。
如下列出 n 、 n -1、 n -2和 n –3四个时间点的EWMA波动率计算式为:

对它们依次代入,即将 σ n -3 代入 σ n -2 ,然后将 σ n -2 代入 σ n -1 ,最后 σ n -1 代入 σ n ,可以得到式(1-24)。
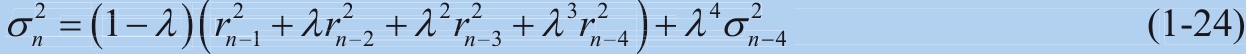
把推导出来的这个等式与图1-17对照,可以看到离当前时刻越远,其权重随指数衰减越厉害。较大的衰减因子,意味着较慢的衰减。以RiskMetrics使用的94%衰减因子为例,前一天的权重为(1 –0.94)×0.94 0 =6%,之前第二天权重为(1 – 0.94)×0.94 1 =5.64%,之前第三天权重则为(1 – 0.94)×0.94 2 =5.30%。
EWMA波动率迭代公式告诉我们,当前一天的波动率是前一天波动率的函数,这也提供了一种用过去波动率预测未来波动率的方法。这种方法,不需要保存过去所有的数值,而且计算量较小,因此在实际中广泛应用。
下面的例子,首先从Fred数据库中提取了标准普尔指数一年的价格数据,然后利用ewm()函数计算指数移动平均。ewm()+函数使得EWMA的计算变得非常方便,但是它并没有直接指定衰减因子,而是提供了与平滑系数 α 的转换关系。衰减因子 λ 与平滑系数 α 有下面的关系。

其中,alpha为平滑系数 α ,且0< α ≤1。
ewm()函数衰减参数介绍如下。com为根据质心指定衰减, α 可以通过式(1-26)计算得到。

span为根据范围指定衰减, α 可以通过式(1-27)计算得到。

halflife为根据半衰期指定衰减, α 可以通过式(1-28)计算得到。

下面的代码,通过指定平滑系数为0.01、0.03和0.06,即衰减因子分别为0.99、0.97和0.94,计算得到波动率曲线。感兴趣的读者,可以修改代码,尝试用其他几种方式来指定衰减。
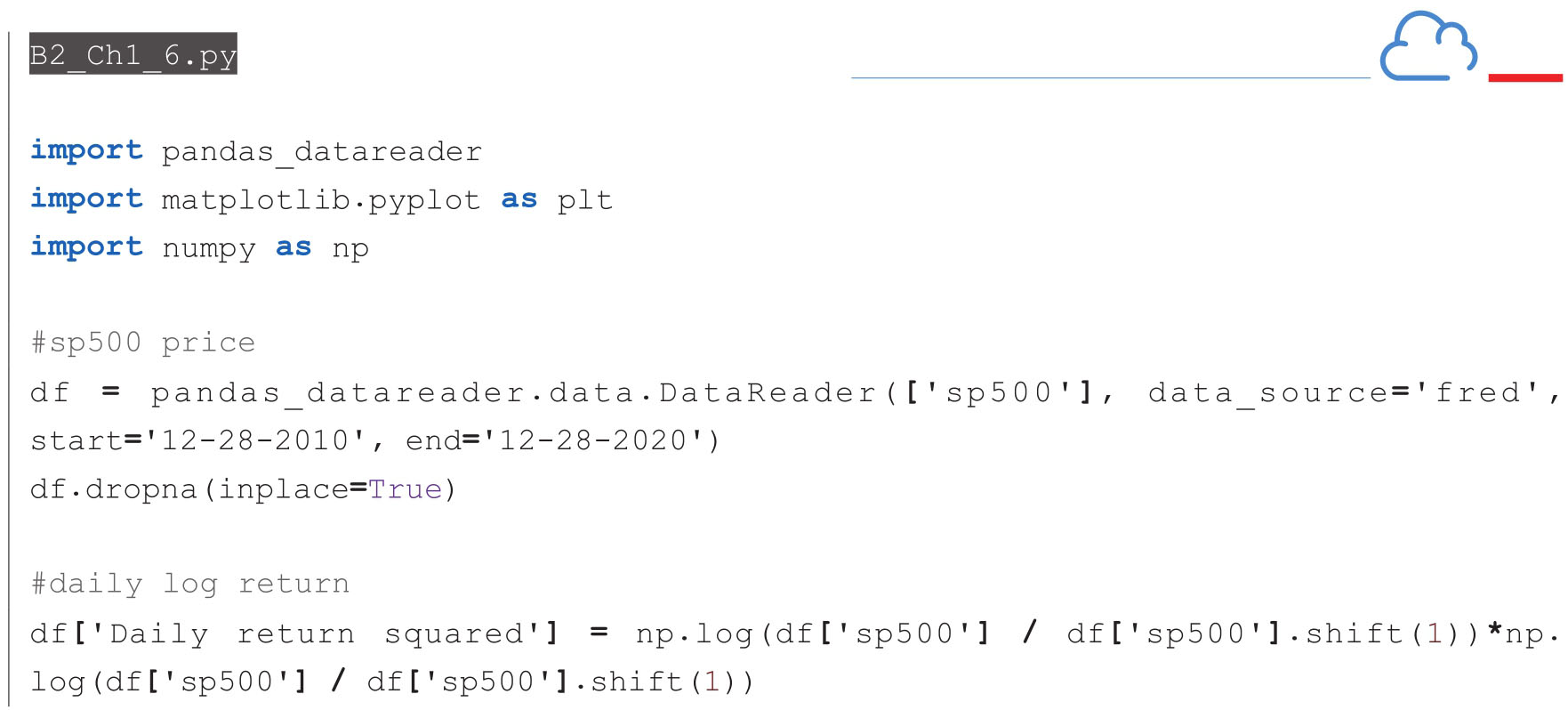
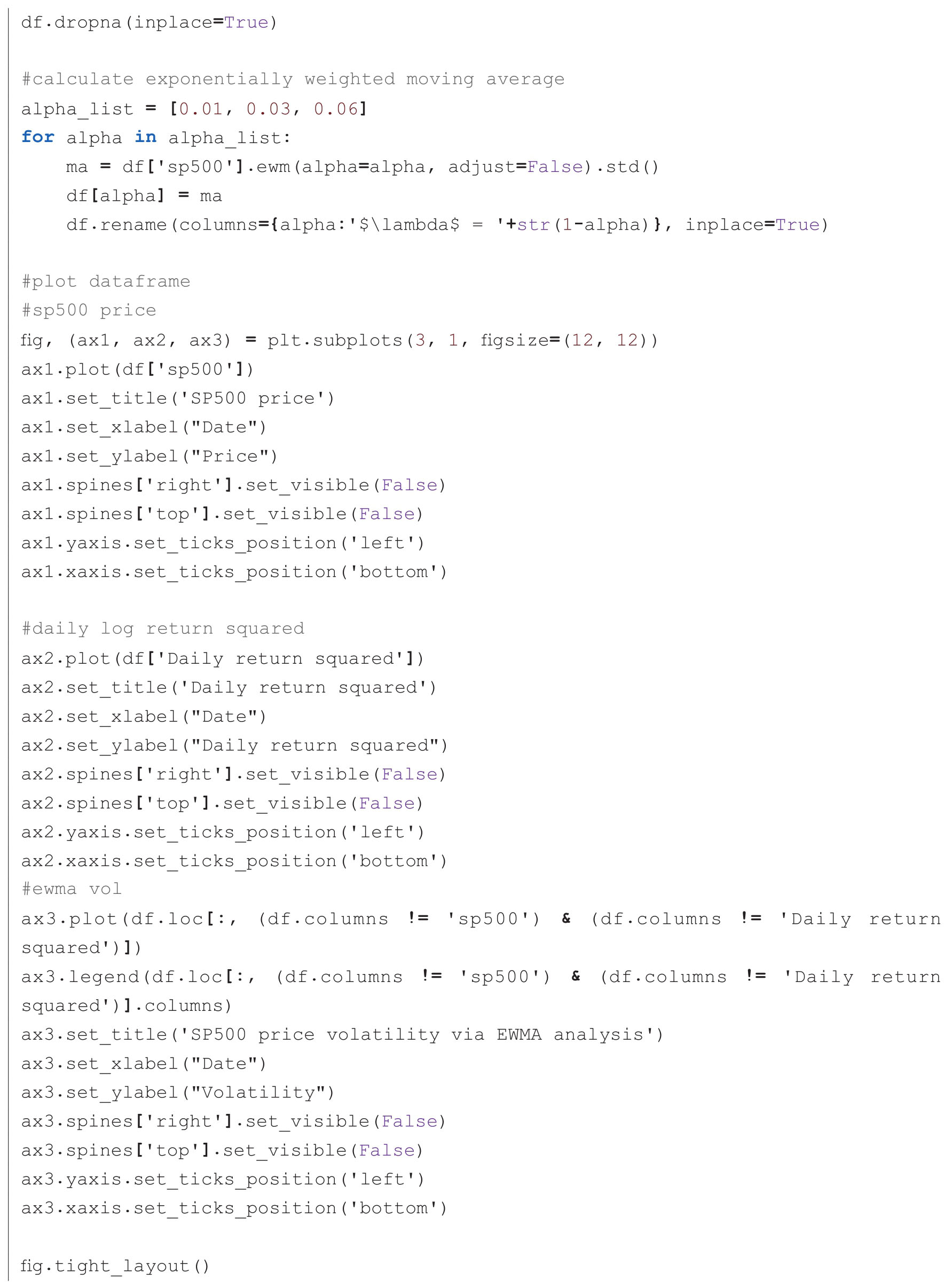
代码运行后,生成图1-17,可见,衰减系数越小,估算的波动率峰值越高,而且波动也会越显著。
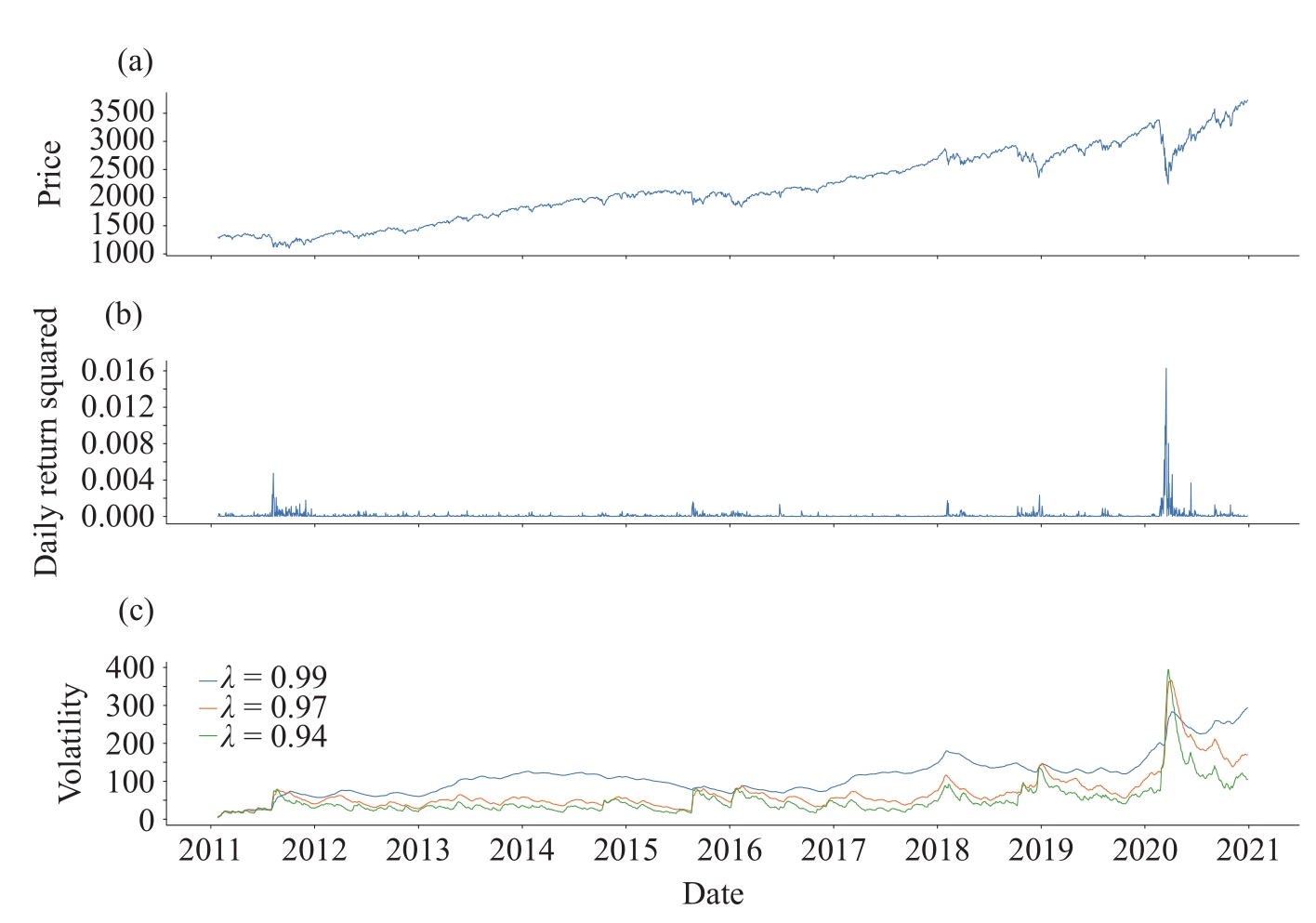
图1-17 指数权重移动平均计算波动率