




在对CARP求最优解的过程中,随着问题规模的增加,解空间的规模会成指数增长,所以又有了大规模的限量弧路由问题(Large-Scale Capacitated Arc Routing Problem,LSCARP)。在车辆路径规划这一问题中,通常任务数目都比较多。与其他算法相比,元启发式算法能够在给定的时间内找到问题的次优解,但是计算需求量很大,花费的时间更多。从算法的角度出发,Memtic算法可以使算法跳出局部最优,获得一个更好的解。
为了解决LSCARP,2014年提出的RDG-MAENS采用了一种分治策略 [30-31] ,把问题分解成很多子问题,分别予以解决,然后再由子问题的解得到完整的解。2015年,有研究者针对RDG-MAENS中个体所属子种群的分配方式不合理问题,提出了一种改进的算法IRDG-MAENS,收敛性有很大提高。 [32]
RGD-MAENS方法采用路由距离分组(Route Distance Grouping,RGD)分解方法将CARP问题的任务集进行分组,使其分解成多个小的子任务集进行求解。这个分组就是路由距离分组,首先定义两个节点之间的距离,这里使用的不是地理信息中的欧几里得距离而是顶点间的路由距离,再利用迪杰斯特拉算法确定两个节点间的最短距离,最后根据路由中所有任务节点的距离确定路由间的距离。两个路由间的距离越小,说明这两个路由越相似,越应该放到一组中。基于这样的定义,分组就变成了对路由间的聚类,两个路由间的距离越小就更可能被归为同一类,这里聚类运用了模糊K-mediods [33] 方法。聚类的关键是路由组中心点的确定,确定好最优的路由中心,才能将相似的路由放到一起进化,节省计算资源,加快收敛速度,提高解的质量。先定义两个任务 z 1 和 z 2 的亲密度为:
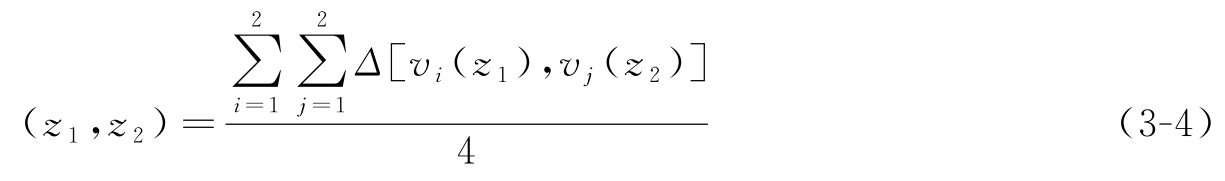
其中, Δ [ V i ( z 1 ), V j ( z 2 )]是任务 z 1 第 i 个终点和任务 z 2 第 j 个终点之间的距离。因此 Δ task ( z 1 , z 2 )就是 z 1 和 z 2 间可能距离的平均值。基于任务距离, s 1 和 s 2 之间的距离定义为:
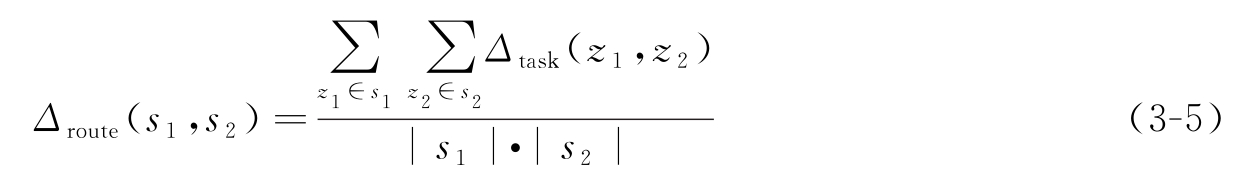
因此 Δ route ( s 1 , s 2 )是任务 z 1 和 z 2 间所有的任务对 s 1 和 s 2 ( s 1 ∈ z 1 , s 2 ∈ z 2 )间的平均距离。再把 Δ route ( s 1 , s 2 )根据 Δ route ( s 1 , s 1 )和 Δ route ( s 2 , s 2 )进行规范化,最终得到任意路由 s 1 和 s 2 间的距离为:

对于LSCARP,其需要分解的数量很大,并且分解后得到的子问题仍然是NP-hard问题。针对这一情况,梅一提出了RDG分解方案。但是,每一代的子问题分解得到的解并不是最好的解,因为RGD没有根据当前群体信息动态地为各个子问题重新分配解,而只是将搜索到的最好的解进行保留,并不参与其他子问题的求解。
在IRDG-MAENS算法中,首先根据RDG算法将大规模的问题进行分解,再对分解后得到的子问题单独求其最优解。在获得子问题最优解后立即用较好的解进行更替并通过邻域共享参与当前子代问题的求解。这不仅能够加快算法的收敛速度,还及时更替每个子问题较好的解,参与该循环和其他子问题的求解,这种方法更利于邻域共享和获得潜在的更好的解。表3.5是更加详细的子问题解的及时更替过程。
表3.5 子问题解的及时更替

遗传算法部分可以采用多目标进化算法(MOEA/D)的算法框架,其思想是,将一个多目标问题通过一定的方法分解为多个子问题,然后同时对这些子问题进行优化,在优化过程中,将考虑其邻域信息,实现在对子问题的优化过程中找到原多目标问题的非支配解。
假设多目标优化函数为 G ( x )=[ G 1 ( x ), G 2 ( x )],通过二维权重系数 α i =( α i 1 , α i 2 )将原多目标问题划分为多个单标优化问题。其中 α i 1 是目标函数 G 1 ( x )的权重系数; α i 2 是目标函数的权重系数。于是,分解后的单目标优化问题的函数可表示为:
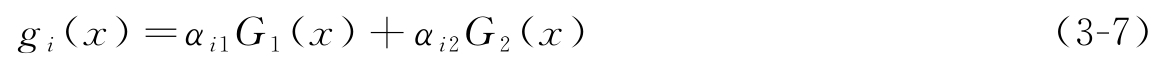
假设有 n 个由两个权重系数构成的权重向量,那么就可以将原多目标问题分解为 n 个子问题。每个子问题都有一个初始解。计算权重间的欧几里得距离,根据该距离为每个子问题选择 T 个邻居,第 i 个子问题的邻居记为 B ( i )={ i 1 , i 2 ,…, i T }。从 B ( i )中随机选择两个个体进行遗传操作产生新解 y ,再更新邻域解:对于所有 j ∈ B ( j ),如果 g i ( x j )< g i ( y ),则 x j = y 。