




第三节
|

|
债券是债务人为了获得资金向债权人出具的、反映债权债务关系的有价证券。债券估价是运用合理的方法对某种债券的内在价值进行合理的估计。影响债券价值的主要因素有:债券的票面利率和发行时的市场利率的高低、债券的期限长短及规定的付息方式等。按照证券估价的基本模型,债券价值就是债券未来现金流入量的现值。债券未来现金流入量包括债券的利息收入及到期归还的本金。对于债券价值的计算,我们可利用前面所介绍的方法,先进行现金流量分析,确定合适的贴现率,然后利用净现值法将其折算成现值,即可得到债券的价值。
下面我们将按照不同的还本付息方式分别来讨论债券的理论价值。
典型的债券是固定利率、每年计算并支付利息、到期归还本金。这种债券的价值估价模型为
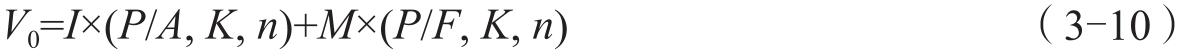
式中: V 0 表示债券价值; I 表示每年的利息; M 表示债券面值; K 表示年贴现率,一般取金融市场中与该债券风险相适应的市场利率; n 表示债券到期前的期限。
下面我们以举例说明说明债券估价的方法。
【例3-8】 康佳集团股份有限公司于2021年1月7日到1月8日非公开发行第一期公司债券(简称“21康佳01”,债券代码:114894)10亿元。期限为3年,票面利率为4.46%,规定起息日期为2021年1月8日,止息日期为2024年1月7日,每年1月8日支付上年利息,到期一次还本。
已知同期发行的3年期储蓄国债年利率为3.85%(作为无风险报酬率),假设投资者对该债券的必要报酬率为5%(其中1.15%视为风险报酬率)。试计算该债券发行时的价值(按一张面值100元计算)。
【解答】 本例中, I =100×4.46%=4.46元, M =100元, K =5%,则
V 0 =4.46×( P / A ,5%,3)+100×( P / F ,5%,3)≈98.53(元)
“按年付息到期一次还本”的债券可以认为是“平息债券”的一种。所谓平息债券,是指利息在债券存续期内平均支付的债券。支付的频率可能是一年一次、半年一次或每季度一次等。如果债券一年支付一次利息,就是康佳集团2021年发行债券的情形。如果一年内支付 m 次利息,则这种债券的价值计算模型为
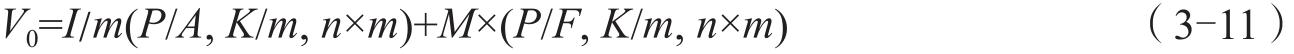
式中:字母的含义同前。
【例3-9】 财政部于2019年5月22日发行2019年记账式附息(六期)国债2790.9亿元,期限为10年,票面年利率为3.29%;规定该国债利息按半年支付,每年5月23日、11月23日(节假日顺延)支付利息,到期一次还本,2029年5月23日偿还本金并支付最后一次利息。该债券于2019年5月27日起在上海证券交易所上市交易。虽然该债券期限较长(为10年),但投资者购买后即可在证券交易所交易,故其流动性风险可以忽视,且债券每半年支付一次利息,因此,我们按照当时我国大多数国有控股商业银行5年期定期存款利率2.75%作为该债券的市场利率。试计算该国债每份(面值为100元)的理论价值。
【解答】 本例中, I =100×3.29%=3.29元, M =100元, K =2.75%, n =10, m =2,则
V 0 =(3.29/2)×( P / A ,1.375%,20)+100×( P / F ,1.375%,20)≈104.69(元)
假如该国债为每年付息,其他条件不变,则其每份的价值应为多少?若为每季度付息,则每份的价值又是多少?请读者计算,并将结果与上例的结果进行比较,仔细体会付息间隔时间的长短对债券价值的影响。
按分期付息到期一次还本的债券在市场中较为常见。显然,随着时间的推延,这种分期付息到期一次还本债券的价值会逐渐上升,到付息前达到最高值,在除息日债券的价格会因为除息而下跌到一个较低的水平,然后再慢慢上升,如此循环。
在我国,公司发行债券也有到期一次还本付息(利随本清)的情形,且不计复利,这种债券的价值计算模型为

式中:字母的含义同前。
【例3-10】 财政部于2021年3月10日至3月19日发行2021年凭证式(第一期和第二期)国债,发行总额为300亿元人民币,其中3年期180亿元,票面年利率为3.8%;5年期120亿元,票面年利率为3.97%。国债从购买之日开始计息,到期一次还本付息,不计复利,逾期兑付不加计利息。该债券不能上市流通。据查,当时发行的同期限可流通国库券的利率水平为:3年期2.76%,5年期3.02%,适当考虑流动性风险,我们确定投资上述两种不可流通国债的必要报酬率分别为:3年期国债3%,5年期国债3.3%。试计算这两种国债每份(面值为100元)的理论价值。
(1)按面值100元3年期国债计算,运用式(3-11), I =100×3.8%=3.8元, M =100元, K =3.3%,则
V 0 =(3.8×3+100)×( P / F ,3%,3)=101.94(元)
(2)同样,可以计算出面值100元5年期国债的价值为
V 0 =(3.97×5+100)×( P / F ,3.3%,5)=101.89(元)
从计算结果可以看出,虽然发行的5年期国债的票面利率高于3年期国债的票面利率,但由于两种债券为到期一次还本付息,且所确定的市场利率略有差异,最后计算得到的3年期国债的理论价值却高于5年期国债。由此可见,债券的价值不仅与债券的票面利率和市场利率有关,而且与利息的支付方式和期限长短也相关。
零息债券是指不支付利息却以低于面值折价出售给投资者的一种债券。它提供给持有者的报酬是资本增值而非利息收入。零息债券是一种较为常见的金融工具创新,最初产生于19世纪80年代。近年来,国外(尤其是美国)的一些大公司也发行此类债券筹集资金。零息债券不支付利息,按票面进行大幅折扣后出售。
例如,J.C.Penny百货公司在1989年曾经发行面额为2亿美元的8年期零息债券,这种债券每份的面额为1000美元,但发行价格仅为332.41美元
 。通俗地讲,就是投资者现在以332.41美元购入一份债券,8年后能够获得1000美元。对发行债券的公司来说,就是现在向别人借入332.41美元,8年后还给人家1000美元。
。通俗地讲,就是投资者现在以332.41美元购入一份债券,8年后能够获得1000美元。对发行债券的公司来说,就是现在向别人借入332.41美元,8年后还给人家1000美元。
尽管我们说,零息债券形式上没有利息,其收益形式是资本利得。但实际上,我们可以将这种资本利得看成是一种利息收益。例如,对于上面的零息债券,我们可以这样来理解:投资者现在购入“面值”为332.41美元的8年期一次还本付息的债券,按单利计算的年利率约为25.10%
 。对发行债券的公司来说就是:现在向别人借入“本金”332.41美元,8年后一次还本付息,年利率为25.10%。因此,零息债券实际上是一种变相的有利息债券,所以我们称其为“零息债券”,而不是“无息债券”。
。对发行债券的公司来说就是:现在向别人借入“本金”332.41美元,8年后一次还本付息,年利率为25.10%。因此,零息债券实际上是一种变相的有利息债券,所以我们称其为“零息债券”,而不是“无息债券”。
零息债券的价值实际上就是以未来到期日的债券价值(面值)以一定的贴现率贴现计算到发行日的价值,其估价模型可以表述为

在投资决策中,我们实际上更需要知道这种债券的实际利率,即根据发行价格(购买价格)和到期价值(面值)倒过来计算利率。对于前面所举的J.C.Penny百货公司发行的零息债券,设实际利率为 K ,可得到下列方程
332.41×(1+ K ) 8 =1000
解得 K ≈14.76%。
也可以这样理解,购买该种债券的投资者相当于获得了14.76%的年收益率。
与股票投资一样,在进行债券投资时,有必要比较各类债券的收益情况,计算出投资收益率,以便做出正确的投资决策。债券投资收益率是一定时期内债券投资收益与投资额的比率。债券投资收益主要包括债券利息收入、债券的价差收益和债券利息的再投资收益。债券利息收入就是根据债券的面值与票面利率计算的利息额;债券的价差收益是债券到期得到的偿还金额(债券面额)或到期前出售债券的价款与投资时购买债券的金额之差;债券利息的再投资收益可以理解为用债券利息再进行投资所得的收益,与前两项不同,它不是债券投资所实际取得的收入,通常在复利计息方式下才予以考虑,单利计息时一般不考虑该项收益。债券投资额是投资时购买债券的金额,主要是购买价格和购买时发生的佣金、手续费等。
不同种类的债券,因计息方式不同、投资时间不同,其投资收益率的计算方法也有所差异。下面我们分别介绍债券的实现收益率和到期收益率的计算方法。
债券的实现收益率是指投资者在一定时期内买进和卖出债券所获得的收益率。一般是将债券作为短期投资而计算的收益率。在这种情况下,由于投资者持有债券期限较短,一般不用考虑资金时间价值因素,只需考虑债券价差及利息收入,将收益额与投资额相比,即可求得债券的现实收益率,其基本计算公式为

式中: K 表示债券实现收益率; V 0 表示债券购买价格; V 1 表示债券出售价格; I 表示债券持有期间的利息。
【例3-11】 利用例3-9的资料,假如有投资者P和投资者Q欲投资2019年记账式附息(六期)国债。两人于2020年7月20日以每张101.84元(当日该债券的收盘价)的市场价格买进2019年记账式附息(六期)国债,投资者P持有该债券至2021年6月4日以101.50元(当日该债券的收盘价)的价格出售,而投资者Q准备持有至到期(2029年5月23日)。已知该国债每年5月23日、11月23日支付利息,到期一次还本,且该债券的年利率为3.29%。试计算投资者P买卖该国债的实现收益率(不考虑债券买卖中的交易费用)。
【解答】 本例中,投资者P因为买进债券后又卖出债券,所以我们可以计算他的实现收益率。而投资者Q买进债券后准备持有至到期,故不能计算其实现收益率。
运用式(3-14), V 1 =101.50元, V 0 =101.84元, I =100×3.29%=3.29元,则
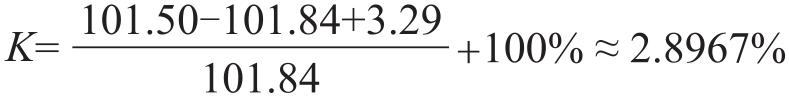
上述计算得到的债券收益率是投资者P从2020年7月20日买进债券至2021年6月4日出售债券合计持有10个半月的收益率,转换为年收益率约为3.31%。以上计算表明,投资者P投资该债券的年实现收益率约为3.31%。
应当注意的是,按照式(3-14)计算的收益率没有考虑时间价值,而且这种收益率是投资者在整个持有期间获得的投资收益率。而投资不同的债券,其持有时间的长短不同,按照式(3-14)计算的收益率不宜直接比较,应当转换为年收益率,再进行比较和选择。
债券的实现收益率表明了债券投资者由于持有债券获得的利息收益和通过买卖债券获得差价的收益水平,这种收益率必须在债券买卖交易完成后才能准确地计算,这对于债券投资决策缺乏指导作用。在债券投资决策时,我们需要事先估计投资某一债券能够获得的收益率,这就是所谓的到期收益率。到期收益率是指按照市场价格购进债券后一直持有至到期日,投资者可获得的年收益率。按照净现值的观点看,到期收益率实际上是使债券未来现金流入量的现值等于债券购入价格的折现率。下面我们按照债券付息方式不同分两种情况加以阐述。
1.分期付息到期还本债券的到期收益率
计算债券到期收益率的方法是求解含有贴现率的方程,即求出使债券投资活动的现金流量的净现值等于零的贴现率,即
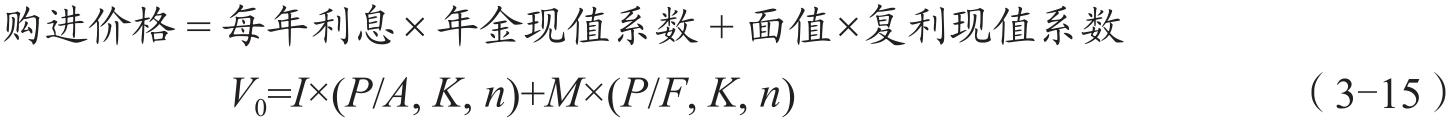
式中: V 0 表示债券的价格; I 表示每年的利息; M 表示面值; n 表示到期的年数; K 表示贴现率(债券到期收益率)。
由于无法直接计算收益率,必须采用逐步测试法及内插法来计算。下面我们来举例说明。
【例3-12】 利用例3-11的资料,投资者Q于2020年7月20日以每张101.84元的市场价格买进2019年记账式附息(六期)国债,并准备持有至到期(2029年5月23日)。我们可以计算投资者Q投资该债券的到期收益率。
【解答】 投资者Q在2020年7月20日以101.84元买进一张该债券,并一直持有至2029年5月23日到期,持有时间为8年10个月零3天,持有期间将在每年的5月23日、11月23日收到1.645元利息,共获取利息18次,到期收回本金100元,投资者Q未来获得的这些现金流量的现值应该等于他买进债券支付的现金。于是得到下列关于(半年)到期收益率 K 的方程
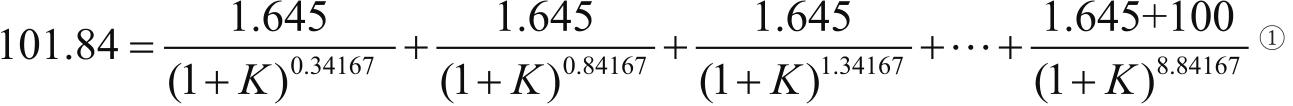
①投资者Q购买债券的日期与首次付息日期相差123天(约0.34167年)。
运用“逐步测试法”(此方法将在本书第四章第三节做详细介绍,此处计算过程省略),求得 K ≈1.65%,转换为年收益率约为3.327%。
2.到期一次还本付息的单利债券到期收益率
计算到期一次还本付息债券的到期收益率相对比较简单,只需要求解下列方程

式中: i 表示债券的票面利率;其他字母的含义同前。
在已知债券购买价格、票面利率、债券面值的情况下,只要通过开方运算便可计算出债券的到期收益率。
【例3-13】 利用例3-10的资料,假如甲某在2021年3月10日购买了财政部于2021年3月发行的5年期国债100000元,票面年利率为3.97%。国债从购买之日开始计息,到期一次还本付息,不计复利。由于该国债不能上市交易,2023年3月10日甲某通过协议方式将该国债以108000元的价格转让给乙某。均不考虑债券买卖中的交易费用。
问题:
(1)如果甲某在2021年3月10日买进该国债后一直持有至到期,计算其到期收益率。
(2)甲某将该国债转让给乙某,其实现收益率为多少?
(3)计算乙某受让该国债的到期收益率。
(1)甲某按面值购买该国债的到期收益率是下列方程的解
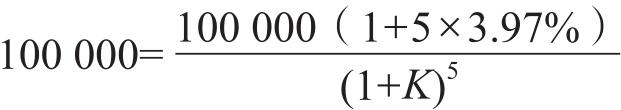
解得 K ≈3.69%。
(2)甲某持有该国债的时间为2年,转让国债的实现收益率有两种算法:
不考虑时间价值的算法,年实现收益率是下列方程的解
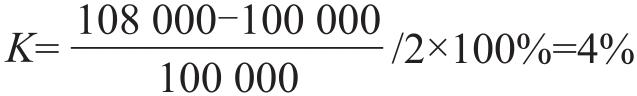
考虑时间价值的算法,年实现收益率是下列方程的解
100000×(1+ K ) 2 =108000
解得 K ≈3.92%。
(3)乙某2年以后从甲某处受让该国债,其到期收益率是下列方程的解
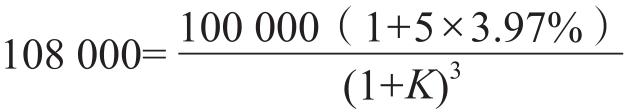
解得 K ≈3.53%。
由计算结果可以看出,甲某购买该债券2年后出售的年投资收益率为3.92%,高于乙某2年后受让该债券的到期收益率3.53%。这说明,甲某在买进债券2年后转让此债券是比较明智的选择,也许甲某是通过精准计算债券投资收益率后做出的转让决策。