




在训练过程中,本地模型可以通过遍历部分数据样本执行更新,以小批量随机方式将数据集的标签和属性信息映射到模型中。为了保证通信参数的隐私性,本节介绍一种差分隐私联邦随机梯度下降算法 [16] (即DP-FedSGD算法)。该算法可在避免训练过程过度震荡的基础上,利用差分隐私算法 [17] 确保用户的隐私安全。
DP-FedSGD算法的框架如图3-3所示,参数及含义见表3-3。
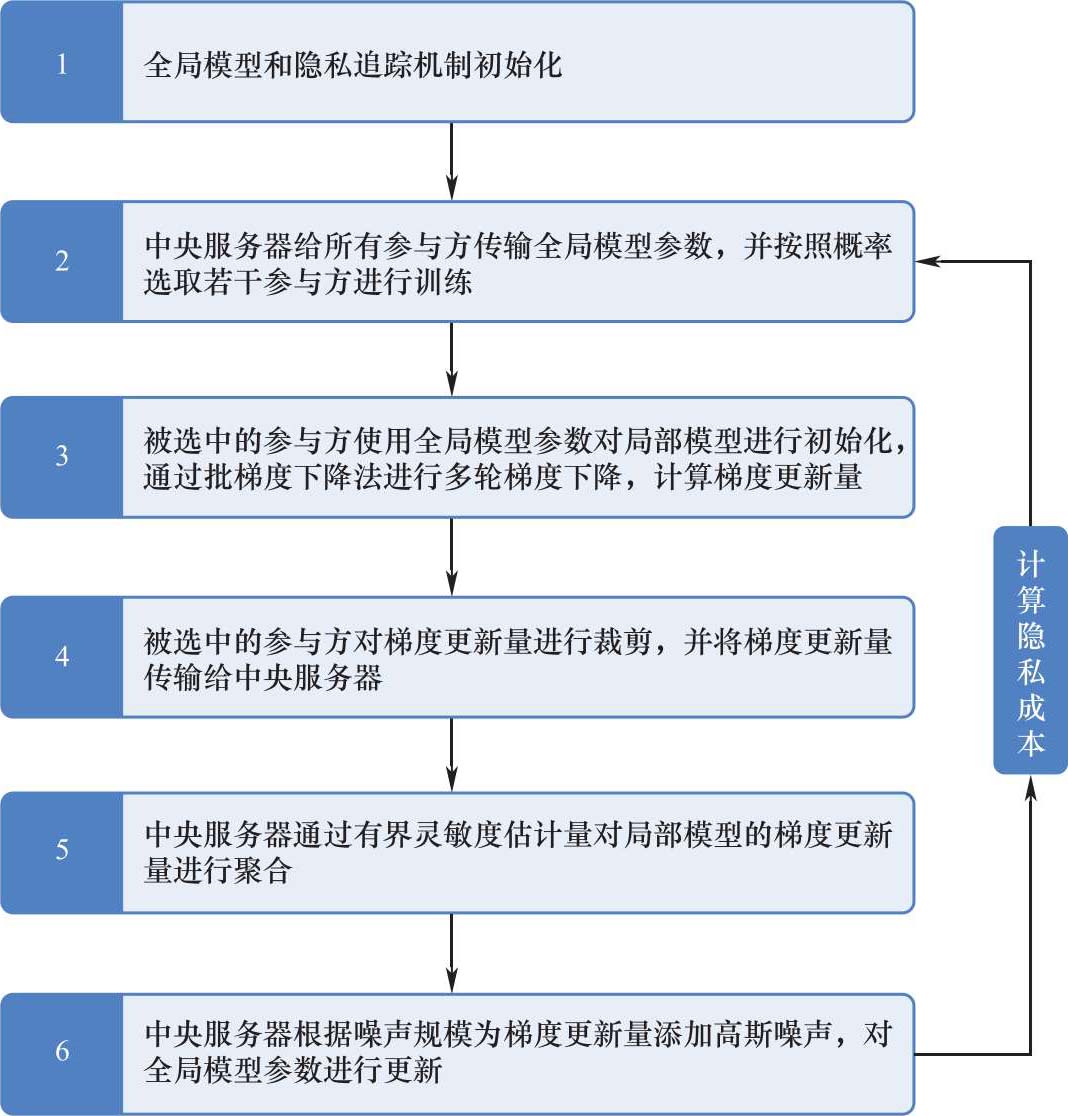
图3-3 DP-FedSGD算法的框架
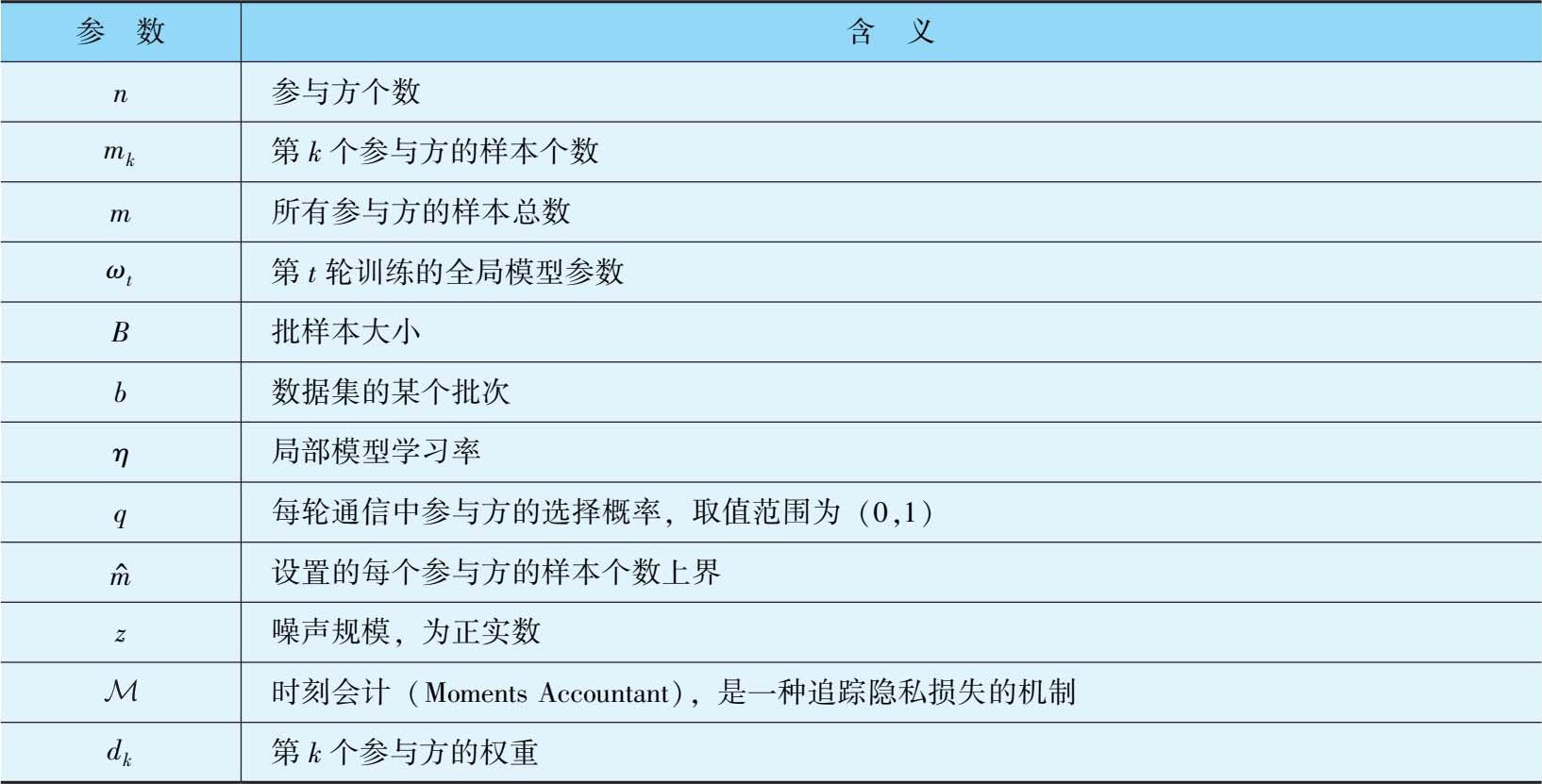
表3-3 DP-FedSGD算法的参数及含义
裁剪方式分2种,即水平裁剪和分层裁剪。
(1)水平裁剪。记参数更新量矢量为 Δ ,将其2-范数的上界设为 S ∈ R ,即:
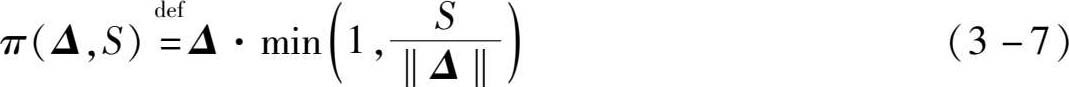
(2)分层裁剪。面向神经网络模型,假设网络总共有 c 层,每一层的参数更新量矢量分别为 Δ (1),…, Δ ( c ),对应的2-范数上界分别为 S 1 ,…, S c ,通过水平裁剪的方法,分别对每一层的矢量进行裁剪:

总体的参数更新量裁剪上界定义为
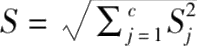 。
。
关于加权聚合方式
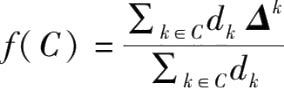 (其中
Δ
k
是参与方
k
的参数更新量)的有界灵敏度(Bounded-sensitivity)的估计量,分为以下2种。
(其中
Δ
k
是参与方
k
的参数更新量)的有界灵敏度(Bounded-sensitivity)的估计量,分为以下2种。
(1)
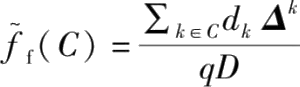 ,其中
,其中
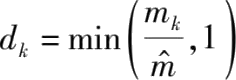 ,是每个参与方的权重;
,是每个参与方的权重;
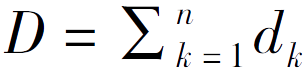 。
。
(2)
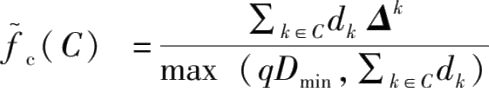 其中
D
min
是预先设置的关于权重和的超参数。
其中
D
min
是预先设置的关于权重和的超参数。
DP-FedSGD算法的流程如算法流程3-3所示。
输入
:全局模型参数初始值
ω
0
,各参与方的样本个数
m
k
,每个参与方的样本个数上界
 ,每轮通信中参与方的选择概率
q
,批样本大小
B
,局部模型学习率
η
,噪声规模
z
,时刻会计
,每轮通信中参与方的选择概率
q
,批样本大小
B
,局部模型学习率
η
,噪声规模
z
,时刻会计
 。
。
输出
:最后一次迭代的全局模型参数
ω
t
+1
,根据
 计算得到的隐私成本值。
计算得到的隐私成本值。
1.中央服务器初始化模型参数
ω
0
和时刻会计
 ,并计算每个参与方的权重
,并计算每个参与方的权重
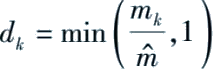 ,
k
=1,2,…,
n
,记
,
k
=1,2,…,
n
,记
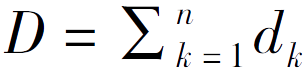 。
。
2.对 t =0,1,2,…,迭代以下步骤直到参数 ω t +1 收敛。
(1)中央服务器将模型的初始参数
ω
t
传输给各参与方,并根据概率
q
分别决定每个参与方是否参与本次迭代,记录参与迭代的参与方集合为
 t
。
t
。
(2)对∀
k
∈
 t
,通过以下步骤进行局部模型的相关参数更新:
t
,通过以下步骤进行局部模型的相关参数更新:
①根据批样本大小 B 从本地数据集中选取一个批次 b 。
②计算局部模型的参数更新量并用选定的裁剪方式进行裁剪:

其中, l ( ω t ; b )是局部模型在参数 ω t 下,批次 b 的损失值。
③将局部模型参数更新量
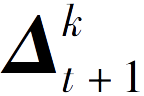 传输给中央服务器。
传输给中央服务器。
(3)中央服务器通过以下步骤对局部模型参数更新量进行聚合:
①根据选定的有界灵敏度估计量,计算聚合结果:
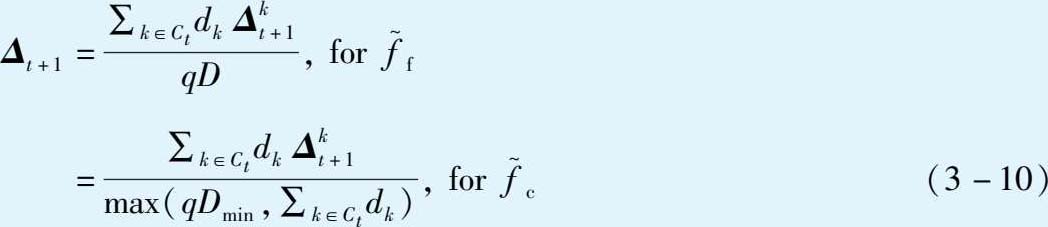
②令 S ←裁剪方式ClipFn中的裁剪上界,根据选定的有界灵敏度估计量和噪声规模 z ,设置高斯噪声的方差:
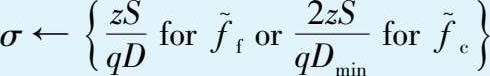
③聚合全局模型的参数为
ω t +1 ← ω t + Δ t +1 + N (0, Iσ 2 )
其中, N (0, I σ 2 )是均值为0、方差为 σ 2 的高斯分布; I 是单位方阵,行数和列数都是参数的个数。
(4)根据
z
和
 计算隐私损失值。
计算隐私损失值。
3.输出
 计算得到的隐私成本值。
计算得到的隐私成本值。