




FedSGD算法 [14] 是联邦学习概念被提出之后的第一个中央服务器优化算法。该算法基于神经网络模型,在所有联邦学习参与方部署相同结构的网络模型,并在每轮训练中通过一次梯度下降更新模型参数,而在每轮通信中,中央服务器随机选取若干参与方进行模型参数聚合,并将聚合后的模型参数传输给所有参与方。通过多轮通信,最终可以在不公开数据的前提下,得到一个适用于所有参与方的全局模型。
FedSGD算法的框架如图3-1所示,参数及含义见表3-1。
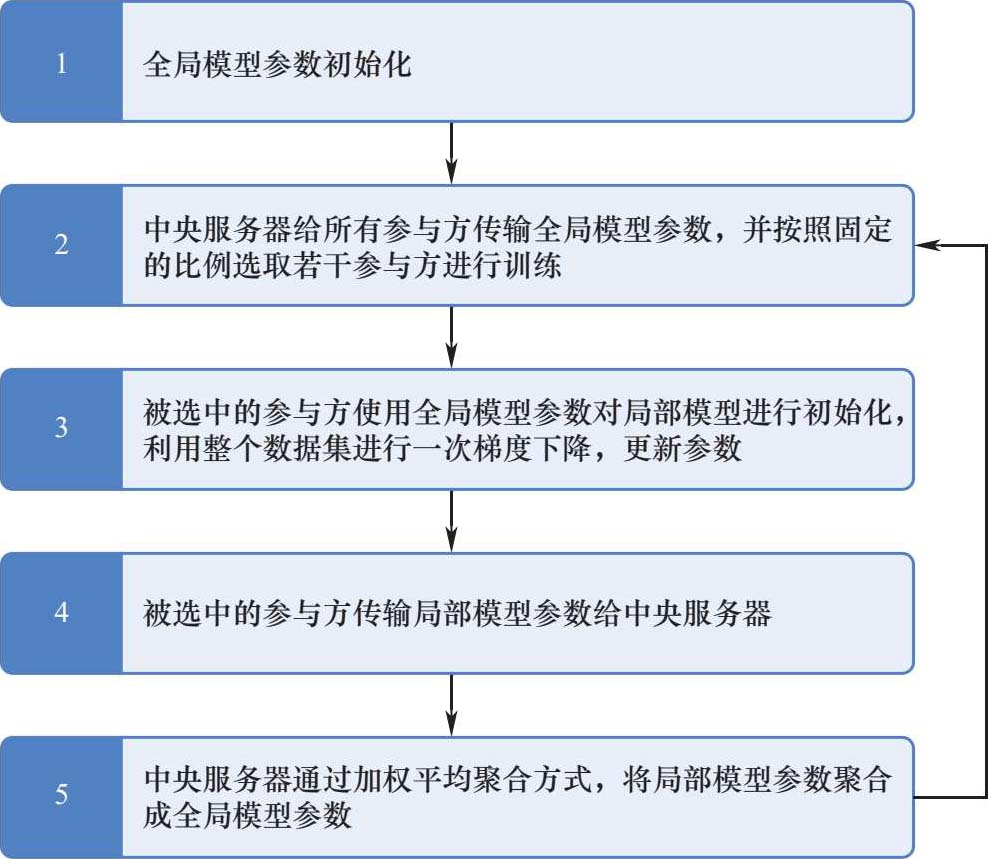
图3-1 FedSGD算法的框架
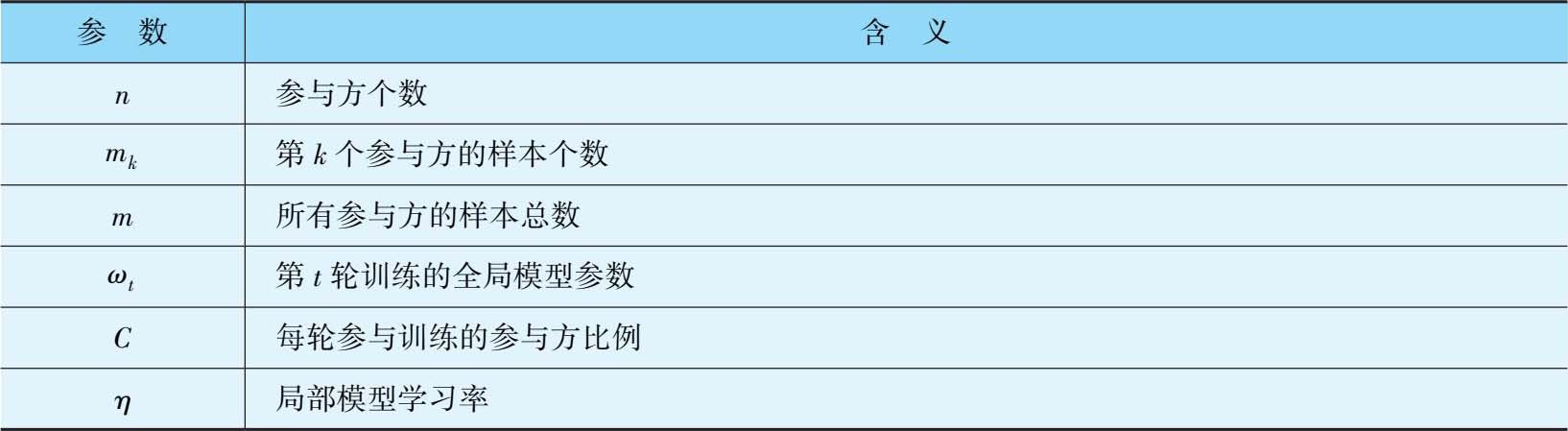
表3-1 FedSGD算法的参数及含义
记联邦学习中参与方 k ( k =1,2,…, n )的目标函数为

其中, P k 是参与方 k 的数据索引集; m k = P k ,是该数据索引集的大小,即参与方 k 的数据集的样本个数; f i ( ω )是样本( x i , y i )在参数 ω 下的目标值,一般取 f i ( ω )= l ( x i , y i ; ω )为某个损失函数,表示样本( x i , y i )在参数 ω 下的损失函数值。
记联邦学习的总目标函数为

其中,
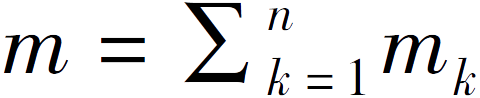 ,是所有参与方的数据集的总样本个数。
,是所有参与方的数据集的总样本个数。
FedSGD算法的流程如算法流程3-1所示。
输入 :全局模型参数初始值 ω 0 ,参与方个数 n ,参与方比例 C ,局部模型学习率 η ,各参与方的样本个数 m k 。
输出 :最后一次迭代的全局模型参数 ω t +1 。
1.中央服务器初始化模型参数 ω 0 ,并传输给所有参与方。
2.对 t =0,1,2,…,迭代以下步骤直到全局模型参数 ω t +1 收敛。
(1)中央服务器根据参与方比例 C ∈(0,1],计算参与第 t 轮迭代的参与方个数。
M ←max( C × n ,1)
(2)中央服务器随机选取 M 个参与方,构成参与方集合 S t 。
(3)对∀ k ∈ S t ,通过以下步骤进行局部模型的相关参数更新。
①使用接收到的模型参数
ω
t
进行模型初始化
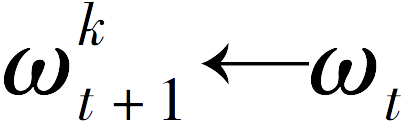 。
。
②使用各自的所有样本,对参数
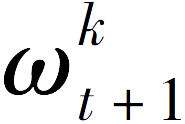 进行一次梯度下降,计算参数
进行一次梯度下降,计算参数
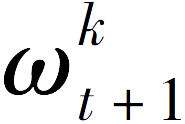 的梯度:
的梯度:

或者计算参数更新值
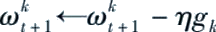 ,其中
η
是学习率。
,其中
η
是学习率。
③将更新好的局部模型参数
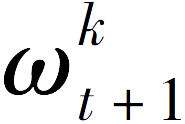 传输给中央服务器。
传输给中央服务器。
(4)中央服务器聚合所有梯度:

或者聚合所有参数更新值
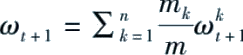 ,并回传给所有参与方。
,并回传给所有参与方。
另外需要说明的是:FedSGD算法名称中的“SGD”并非指局部模型的参数更新使用了随机梯度下降法,这里的“随机”(Stochastic)是指在每轮通信中,参与梯度聚合的参与方是随机选取的,而每个参与方进行局部模型参数更新时使用的是梯度下降法。