




阿莱(Allais,1953)提出的著名悖论挑战了冯·诺伊曼-摩根斯坦理论框架。假设有一组彩票,每个彩票都是从包含100个标记为0~9的球的瓮中抽出一个球。表1.1显示了在4个不同的彩票 L a 、 L b 、 M a 和 M b 中抽中每个球所能获得的奖金。
彩票 L a 提供50美元的确定奖金,而彩票 L b 有89%的概率能中50美元,10%的概率能中250美元,1%的概率没有任何奖金。面对这种选择,许多人相较 L b 更喜欢 L a ,尽管彩票 L b 的预期奖金更高。彩票 M a 有11%的概率赢得50美元,89%的概率得不到任何收益,而彩票 M b 有10%的概率赢得250美元,90%的概率什么也得不到。面对这种选择,许多人相较于 M a 更喜欢 M b 。
对效用理论的挑战是选择 L a 而不是 L b ,同时选择 M b 而不是 M a ,这违反了独立性公理。通过表1.1可以看到, L a 和 L b 之间的唯一区别在于标记为0~10的球;标记为11~99的球在这两个彩票中是相同的; M a 和 M b 也是如此。根据独立性公理,绘制球11~99的奖励应该与 L a 和 L b ,以及 M b 和 M a 之间的选择无关。但如果是这种情况,那么两个选择应该相同,因为如果只考虑球0~10,则 L a 具有与 M a 相同的奖励,并且 L b 具有与 M b 相同的奖励。
表1.1 阿莱悖论

关于这一悖论,人们争论已久。要么是人们容易被误导(但可以通过教育矫正),要么需要放弃独立性公理。放宽这个公理必须小心谨慎,以避免产生进一步的悖论[ Chew (1983), Dekel (1986),Gul(1991)]。 [1] 最近的动态决策模型,特别是本书第6.4节中讨论的爱泼斯坦- 兹恩偏好(1989,1991), 在跨时间的情况下放宽独立性公理,谨慎处理以保持时间一致决策。
拉宾(2000)批评了效用理论,理由是它不能解释人们对小型赌博表现出明显的厌恶,却对大型赌博没有极其强烈的厌恶情绪。这是因为可微效用具有二阶风险规避。
要理解拉宾批评,可以假设一场赌博,能以1/2的概率赢得11美元,并以1/2的概率输掉10美元。随着边际效用递减,胜利的效用至少为11 u′ ( W 0 +11)。损失的效用成本最多为10 u′ ( W 0 -10)。因此,如果一个人拒绝这个赌博,我们必须有10 u′ ( W 0 -10)>11u′( W 0 +11),这意味着:
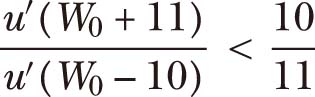
现在假设这个人在 W 0 +21的初始财富水平上拒绝同样的赌博。那么:
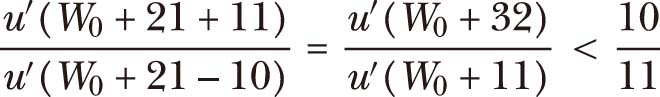
结合这两个不等式:
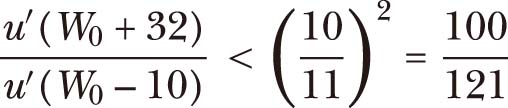
如果进行重复迭代,那么会在高财富水平上得到极小的边际效用,这将导致人们拒绝显然极具吸引力的赌博。
表1.2摘自拉宾(2000)的表 I ,原注释为“如果对所有财富水平,拒绝在50-50概率上输100美元/赢 g 的赌博,也将拒绝在50-50概率上输 L /赢 G 的赌博; G 的值在表中给出”。 g 值为列标题, L 值为行标题,而表格的单元格表示 G 。换句话说,每向右移动一列时,一个参与者就会拒绝更多有利可图的小型赌博;每向下移动一行时,都对应一个更大的可能损失;而单元格中是引诱参与者下注所需的奖金。∞意味着他将拒绝最高奖励为任何有限数值的赌博,无论奖励有多大。
表1.2 摘自拉宾(2000)表I(单位:美元)
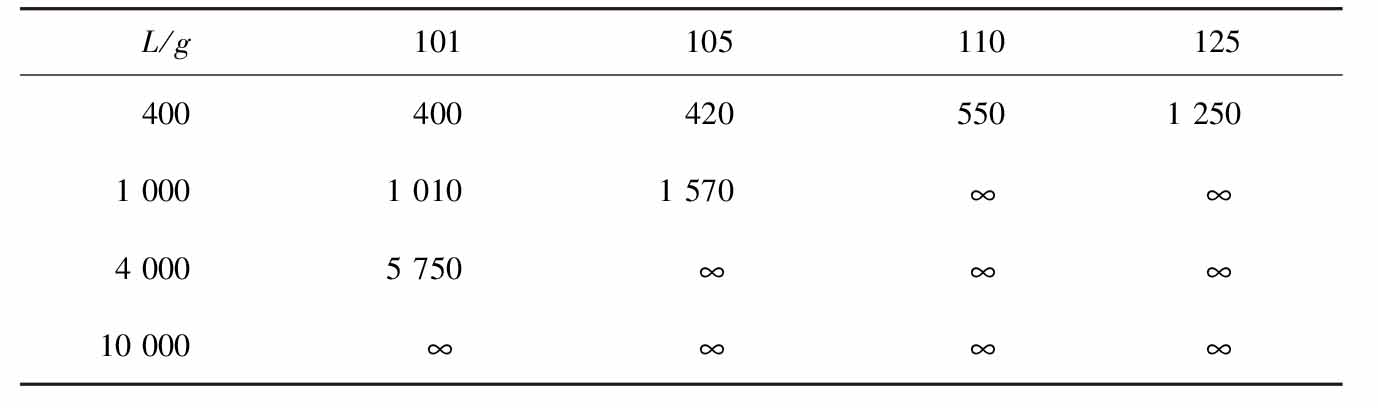
表1.3 摘自拉宾(2000)表II(单位:美元)
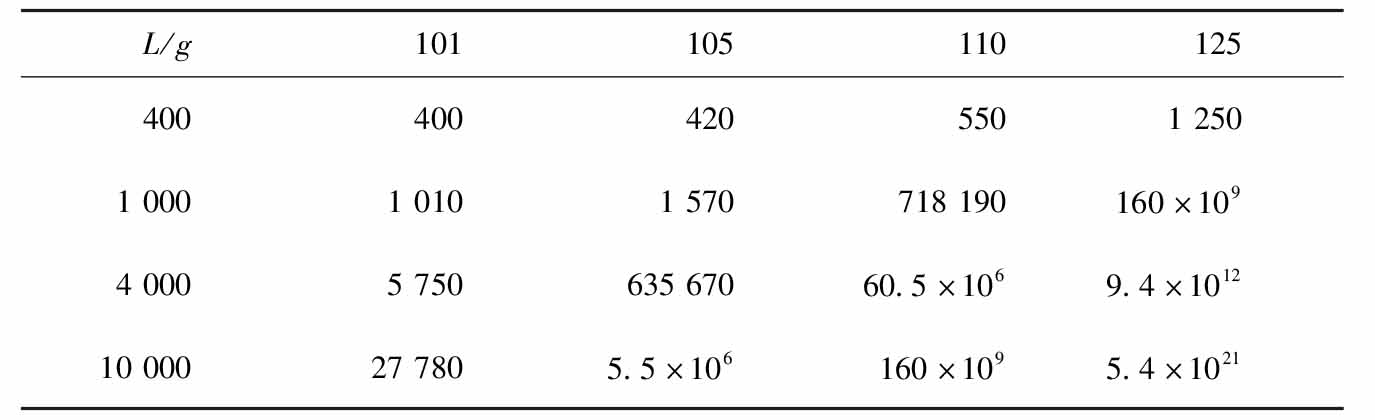
第一个显而易见的问题是,参与者如何能够对任意大的奖金没有反应,拒绝承担有限损失的风险。这个问题将作为非正式练习,并将在本章末尾回答。作为提示,表1.3摘自拉宾(2000)的表II。这个表与表1.2的唯一区别在于,这里的数字都限定于特定的初始财富水平(290 000美元),而表1.2中对50-50概率损失100美元 / 赢得 g 的赌博的厌恶被认为仅适用于高达300 000美元的财富水平。
拉宾批评表明,预期效用的标准理论无法解释在很大范围的财富水平上对小型赌博的风险规避。在任意财富水平上,人们可以通过放宽效用是二次可微的假设来增加对标准理论中的小型赌博的厌恶,允许效用函数中的突兀点使式(1.25)中给出的风险溢价的标准公式无效。这种突兀点使得风险厌恶局部无限,并使得小型赌博的风险溢价与其标准差而非其方差成正比;与二次可微效用相应的“二阶”风险厌恶相比[Segal和Spivak(1990)],这被称为“一阶”风险厌恶。然而,这种方法只会在单点上增加小型赌博的厌恶,而如果一个参与者反对一系列财富水平下的小型赌博,拉宾的论证(不假设效用函数的二次可微性)仍然适用。
为此,经济学家和心理学家已经探索了具有参考点的模型,其中效用来自相对于参考点的收益或损失,该参考点通常设定为等于当前财富。这使得效用函数中的突兀点可移动,让它始终发挥作用并且在任意初始财富水平处导致一阶风险厌恶。
最著名的例子是卡尼曼(Kahneman)和特沃斯基(Tversky)在1979年提出的前景理论,它不仅在参考点上存在拐点,而且有两个其他特征符合对风险态度的实证证据:偏好函数在获得收益时为凹,在遭受损失时为凸(风险爱好),以及当概率很小时,主观概率大于客观概率。前景理论偏好函数的标准参数化是:
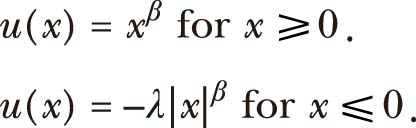 (1.37)
(1.37)
其中, x=W-W REF ,表示财富与参考财富水平之间的差异。我们假设 0 <β<1来确定遭受损失时的凸度和获得回报时的凹度,并且 λ >1,以在参考点处产生突兀点。Gul(1991)中令人失望的厌恶偏好也将参考点附近突兀点设置为赌博的内生确定性等价[Backus、Routledge和Zin(2004)]。
Barberis、Huang和Thaler(2006)指出,即使存在这些偏好也不能对小的延迟赌博产生实质性的厌恶。在决定进行赌博和结果尘埃落定之间的时间段内,参与者将面临其他风险,并将这些与正在进行的赌博合并。如果赌博与其他风险不相关,那就是分散化的。实际上,对于延迟赌博,参与者将具有二阶风险规避。为了解决这个问题,Barberis等人争辩说人们独立地对待每一个赌博,也就是说,他们“目光狭隘”。
在本书中,我们将继续使用标准效用函数,尽管它们无法解释对小风险的厌恶。这也是我的观点,即该理论对于资产定价问题是有用的,与拉宾(2000)承认它“很可能是极大规模保险选择的有用模型”一致。有人可能会以物理学类比,其中重力在宏观角度上极为重要,尽管在亚原子尺度上其他种类的力变得更为重要,而重力变得可以忽略不计。
最后,值得注意的是,可以扩展预期效用理论,以得到对中等规模和大规模风险的厌恶差异。尤其是,Chetty和Szeidl(2007)表明,“消费承诺”(用于调整消费比例的固定成本)相对于大型赌博提高了对中型赌博的风险厌恶,而大型赌博的极端结果被认为支付调整消费所需的成本是值得的。