





思考问题
中学阶段我们已经学会了求解简单的线性方程组。例如,设二元线性方程组
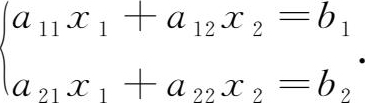
当 a 11 a 22 - a 12 a 21 ≠0时,用消元法可以求得上述方程组的解为:
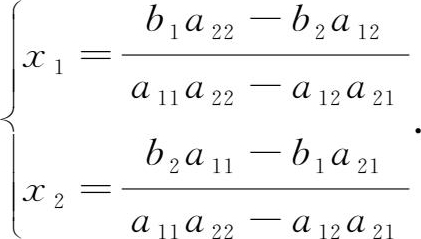
如何更方便地记忆上述方程组的解呢?为此我们引入二阶行列式的概念。
定义1.1.1
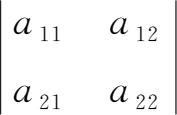
称为 二阶行列式 ,它由2 2 个数构成,表示一个算式,其值为 a 11 a 22 - a 12 a 21 ,即
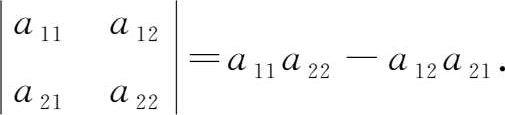
其中,数 a ij ( i =1,2; j =1,2)称为行列式的元素。元素 a ij 的第一个下标 i 称为行标,表明该元素位于第 i 行,第二个下标 j 称为列标,表明该元素位于第 j 列。
把 a 11 到 a 22 的对角线称为 主对角线 , a 12 到 a 21 的对角线称为 副对角线 。
二阶行列式的值是主对角线上的元素之积减去副对角线上的元素之积,称之为二阶行列式的对角线法则。
利用二阶行列式的定义,对于【思考问题】中的二元一次线性方程组
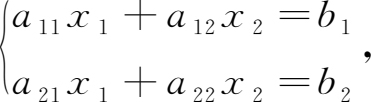
记
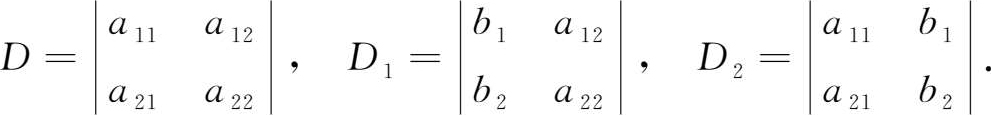
若 D ≠0,那么

这里的分母 D 是由方程组的系数所确定的二阶行列式(称为系数行列式), x 1 的分子 D 1 是用常数项 b 1 , b 2 替换 D 中第一列的元素所得的二阶行列式, x 2 的分子 D 2 是用常数项 b 1 , b 2 替换 D 中第二列的元素所得的二阶行列式。
小试牛刀
例1.1.1 求解二元线性方程组
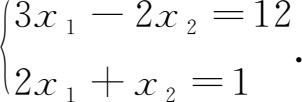
解 因为
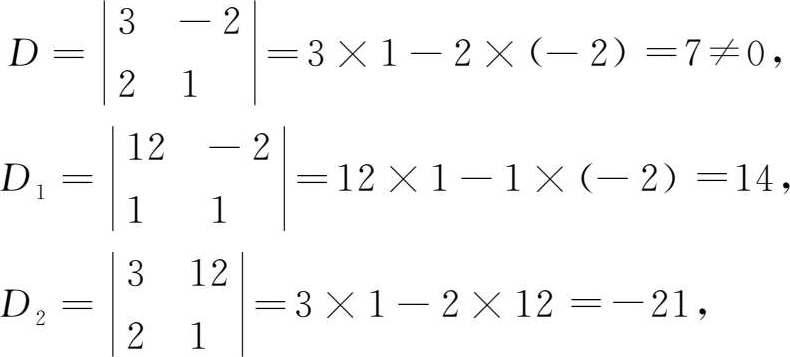
所以方程组的解为
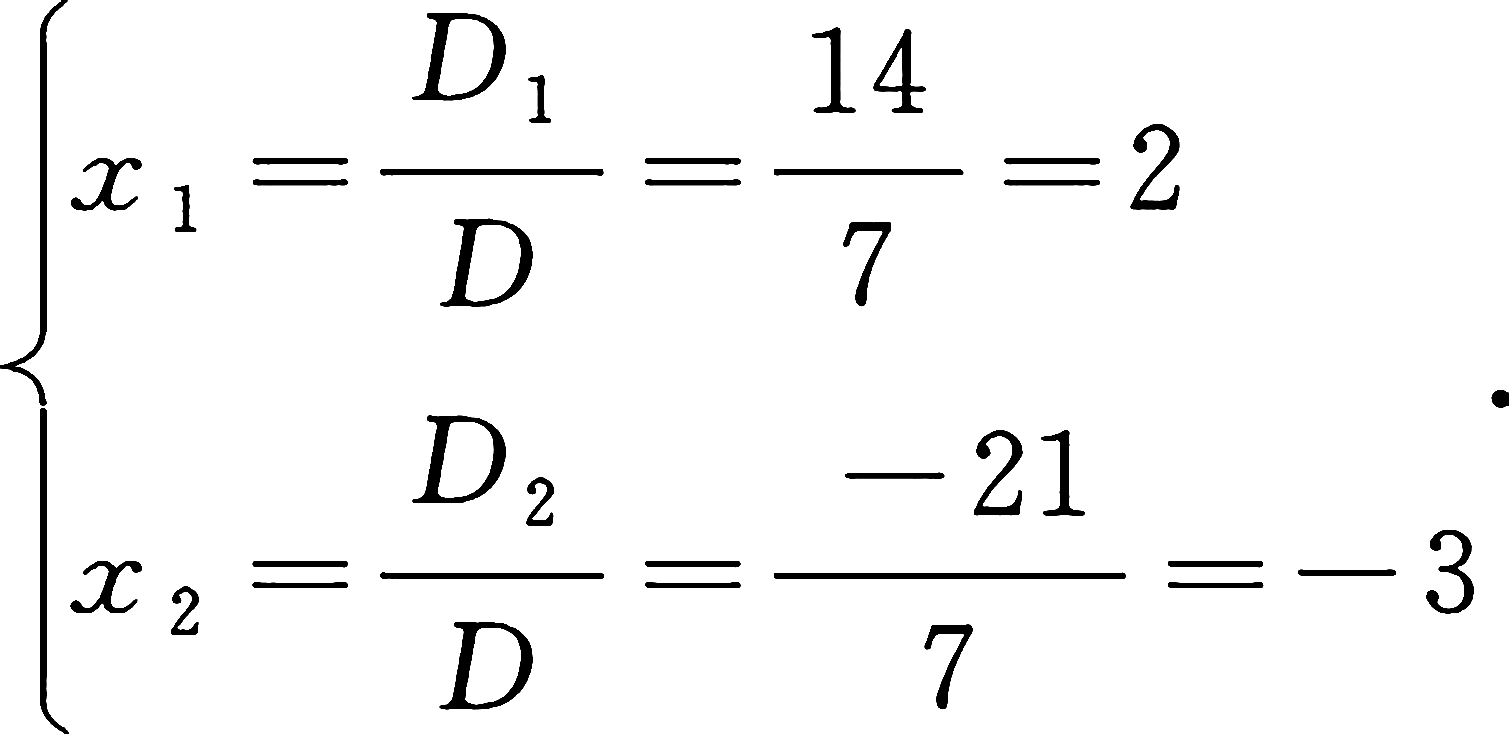 D
7
D
7
与二阶行列式类似,可以定义三阶行列式。
定义1.1.2

称为 三阶行列式 ,它由 3 2 个数构成,表示一个算式,其值为 a 11 a 22 a 33 + a 12 a 23 a 31 + a 13 a 21 a 32 - a 11 a 23 a 32 - a 12 a 21 a 33 - a 13 a 22 a 31 ,即
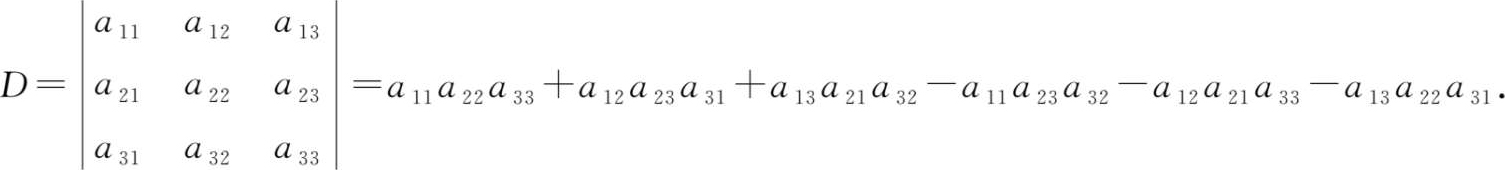
三阶行列式的值是六项代数和,每项是三个元素的乘积,可借助图1-1记忆,其中实线上的三元素的乘积前是正号,虚线上的三元素的乘积前是负号。这种方法称为三阶行列式的对角线法则。
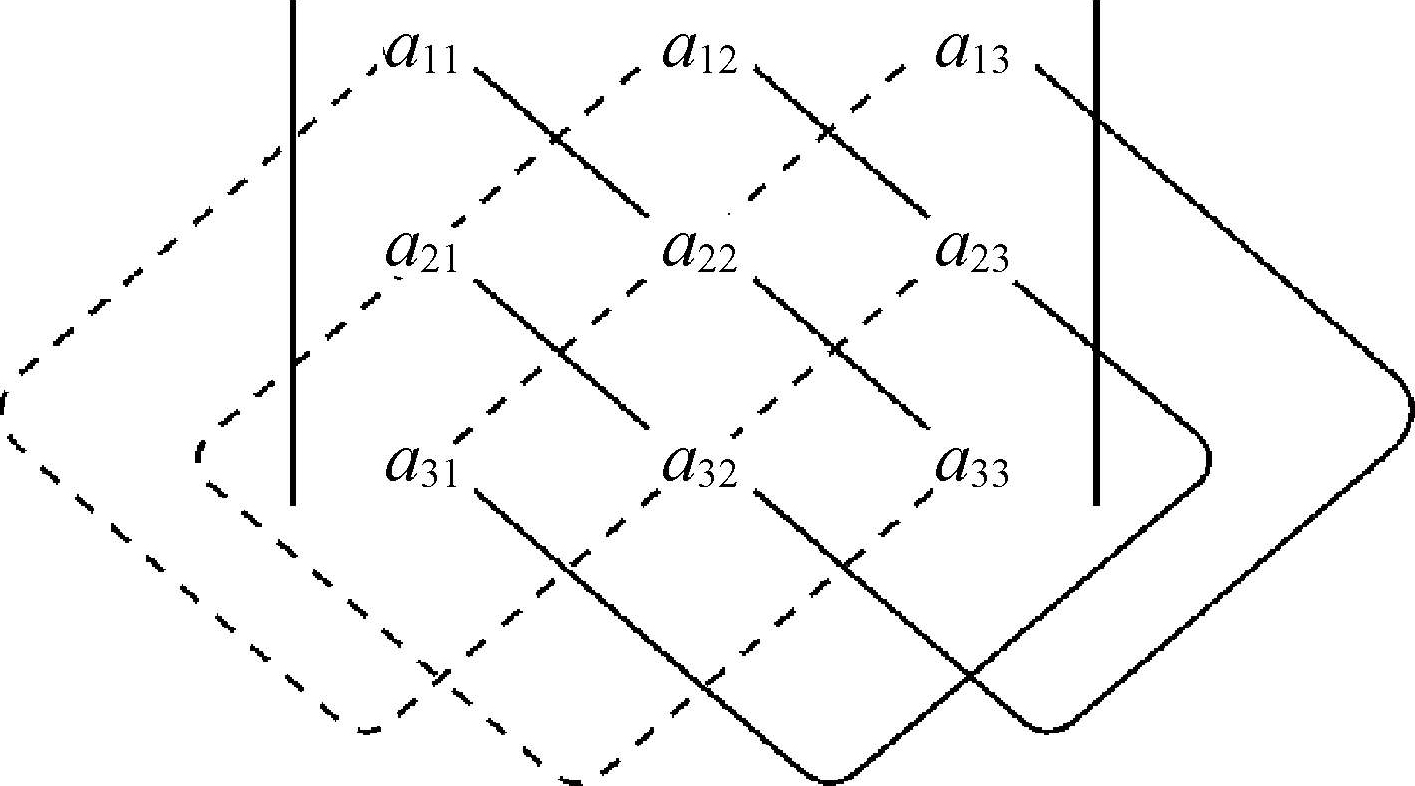
图1-1
小试牛刀
例1.1.2 计算三阶行列式
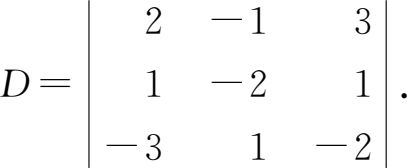
解 D =2 × (-2) × (-2)+(-1)×1 × (-3)+3×1×1-2×1×1-(-1)×1 × (-2)-3 × (-2) × (-3)=8+3+3-2-2-18=-8。
大展身手
例1.1.3 解方程
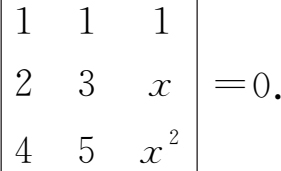
解 方程左端的三阶行列式
D =3 x 2 +4 x +10-5 x -2 x 2 -12= x 2 - x -2,
由 x 2 - x -2=0,解得 x 1 =-1, x 2 =2。
由二阶行列式和三阶行列式的定义,不难发现如下关系式。
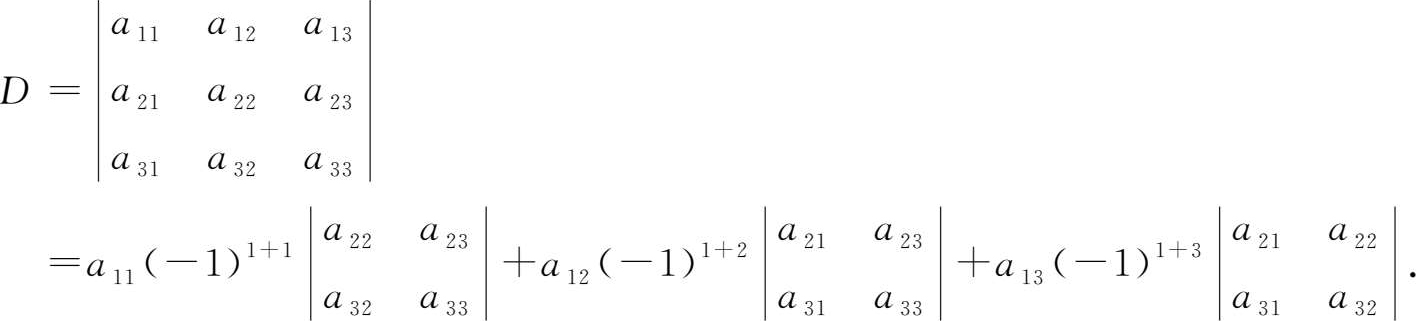
定义
1 .1.3 称
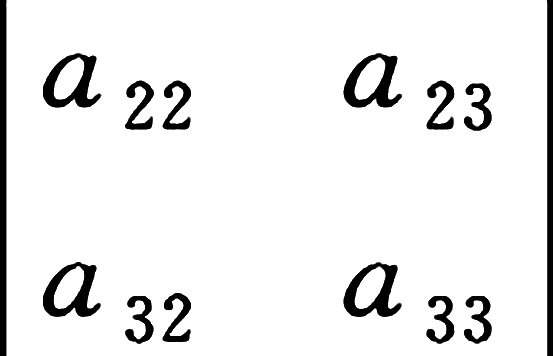 为三阶行列式
D
中元素
为三阶行列式
D
中元素
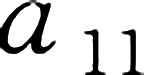 的
余子式
,记作
M
11
,即
的
余子式
,记作
M
11
,即
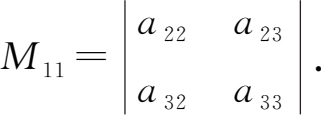
元素 a 11 的 余子式 是原三阶行列式 D 中划去元素 a 11 所在的第一行和第一列后剩下的元素按原来顺序组成的二阶行列式。
类似地,分别记 a 12 , a 13 的余子式为
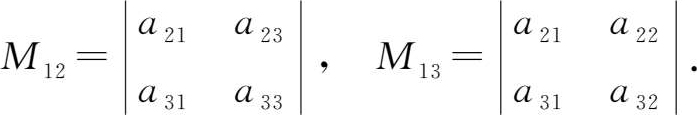
类似地可以定义三阶行列式其他元素的余子式。
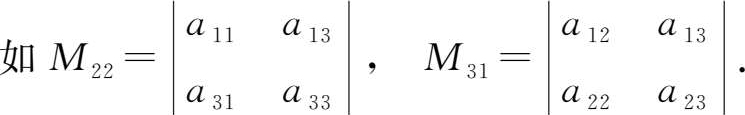
定义1.1.4 称
A ij =(-1) i + j M ij ( i =1,2,3; j =1,2,3)
为三阶行列式 D 中元素 a ij ( i =1,2,3; j =1,2,3)的 代数余子式 。
因此,三阶行列式也可以表示为
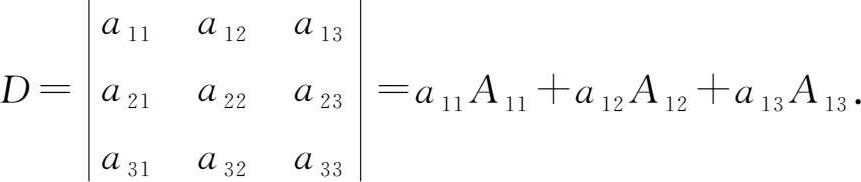
这样,求三阶行列式的问题就可以转化为求二阶行列式的问题,这种求行列式的方法称为 降阶法 ,上面式子的右端称为按行列式 D 的第一行展开的展开式。
降阶法是可以按任意一行(列)展开的,即任一行(列)各元素与其对应的代数余子式的乘积之和。
小试牛刀
例1.1.4 利用降阶法计算三阶行列式
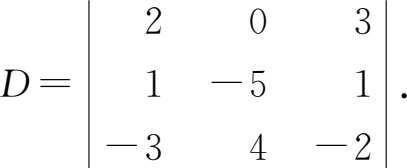
解法1 按第一行展开
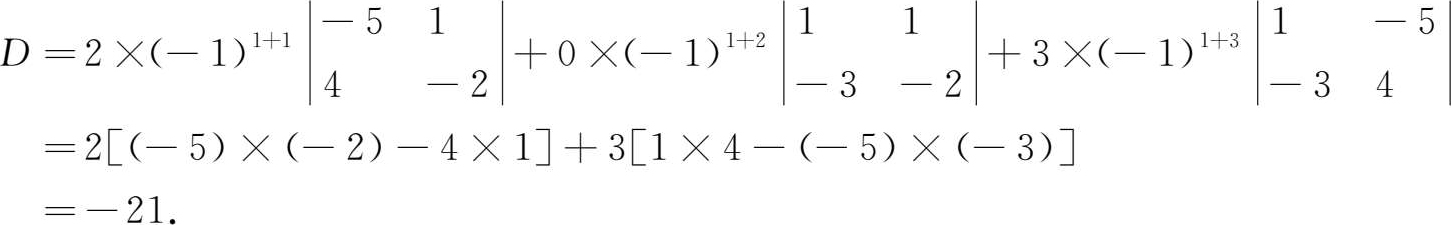
解法2 按第二列展开
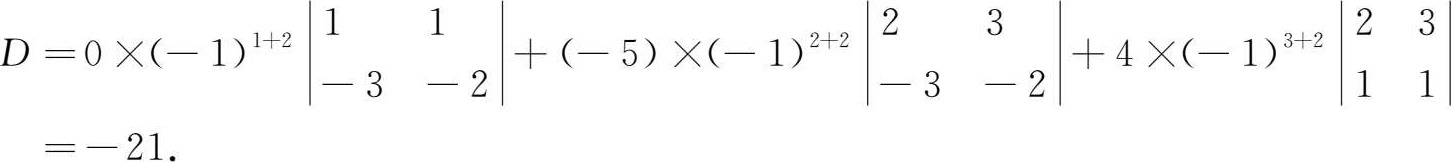
仿照二、三阶行列式,可以把行列式推广到一般情形。
定义1.1.5
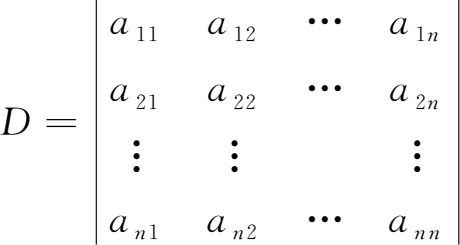
称为 n 阶行列式 ,它由 n 2 个数构成,代表一个算式,其值为
①当 n =1时,规定 D =| a 11 | =a 11 ;
②当 n ≥2时,均可用降阶法计算,即行列式按任意一行(或列)展开,得
D =a i 1 A i 1 + a i 2 A i 2 +…+ a in A in ( i =1,2,…, n )
或
D = a 1 j A 1 j + a 2 j A 2 j +…+ a nj A nj ( j =1,2,…, n )。
对于 n 阶行列式,元素 a ij ( i =1,2,3,…, n ; j =1,2,3,…, n )的余子式和代数余子式的定义与三阶行列式的余子式和代数余子式的定义类似。
例如 行列式,
 中元素
中元素
 的子式和子式余代数余分别是8 -1 -2 4
的子式和子式余代数余分别是8 -1 -2 4
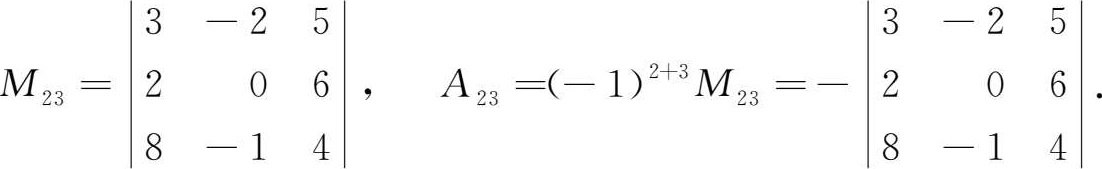
小试牛刀
例1.1.5 计算四阶行列式

解
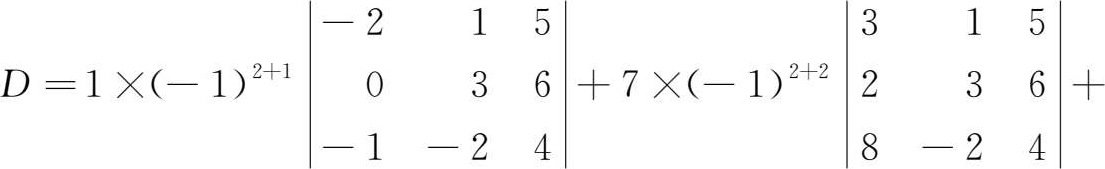
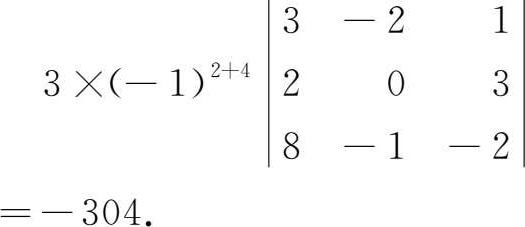
利用降阶法求行列式的值,选择零元素多的行(列)展开。
例1.1.6 计算四阶行列式
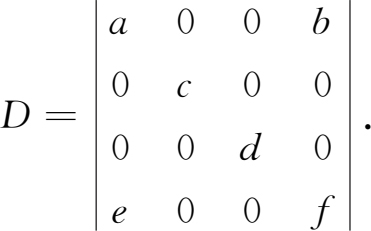
解
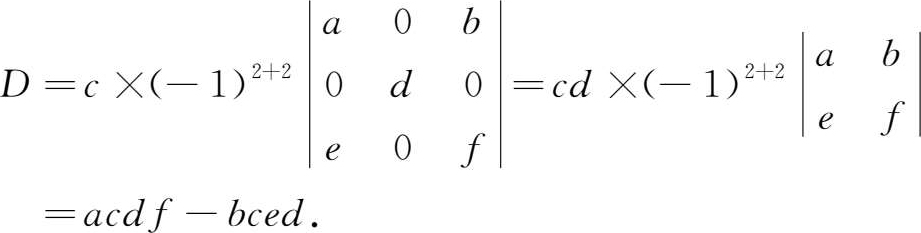
大展身手
例1.1.7 计算 n 阶下三角行列式

解
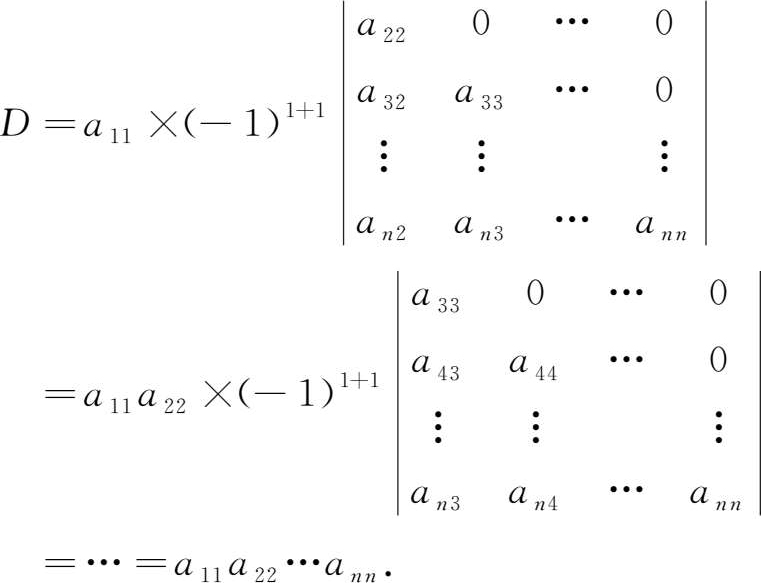
例1.1.8 计算 n 阶上三角行列式

解
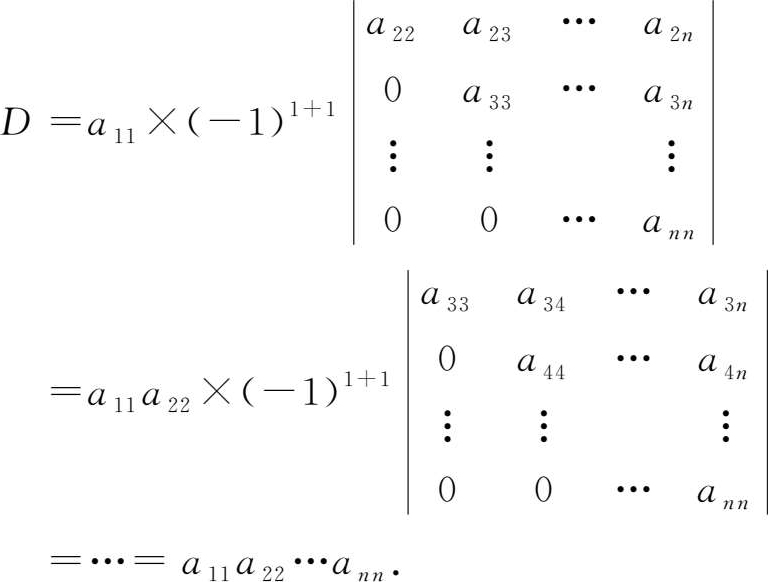
类似的,对角行列式
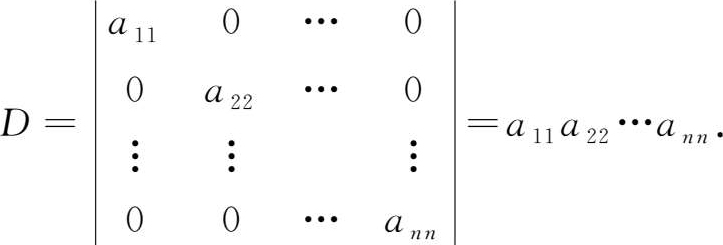
n 阶上(下)三角行列式、对角行列式的值等于主对角线上各元素的乘积。
小试牛刀
1.计算下列行列式:

大展身手
2.解下列方程:
