




自然界中,经常可以看到物体在某中心位置附近做一种周期性的往复运动.这种物体在平衡位置附近所做的往复运动称为 机械振动 ,简称 振动 .
振动是一种常见的物理现象,各种机械运行时的振动、水波的振动、乐器的弦振动等,都是最常见的例子.振动的特点在于往复的周期性运动.在物理学领域内,还有一些物理现象或物质运动,描述这些现象或运动的物理量,也是在某一数值附近做周期性的变化,例如交流电的电流和电压、光波在空间某点的电场强度或磁场强度等.尽管这些现象不是机械振动,但描述它们的方式和运动方程是完全一样的.对于这样的一些运动,我们也称为振动.
物体做振动时,振动物体的位置坐标随时间的变化规律为余弦(或正弦)函数,则称物体的振动为 简谐振动 .简谐振动是一种最简单、最基本的振动,许多复杂的振动都可以分解为简谐振动的合成.了解和掌握了简谐振动对于掌握其他各种复杂的振动具有重要意义.
接下来我们以弹簧振子为例详细讨论简谐振动.如图4-1所示,长度为 l 0 的轻质弹簧(质量可以忽略不计)的一端固定,另一端连接一个质量为 m 的小球,放置在光滑的水平面上.当小球在水平方向不受外力作用时,弹簧处于自然长度 l 0 ,小球处于平衡位置 O 点.然后对小球施加一个向右的作用力,将小球拉至 A 点,然后无初速地释放,小球将在弹簧弹性恢复力的作用下从 A 点向 O 点运动.弹性恢复力指向 O 点,小球速度逐渐增大.当小球到达 O 点时,弹性恢复力为0,小球不受力的作用,但小球在惯性的作用下,通过 O 点继续向左运动.于是,弹簧开始被压缩,弹性恢复力仍然指向 O 点.在这个弹性恢复力的作用下,小球速度逐渐减小,直到减小到零并到达左边最远点 B 点.从 B 点小球再次开始加速向 O 点运动,整个运动过程与小球从 A 点向 B 点的运动情况相似.
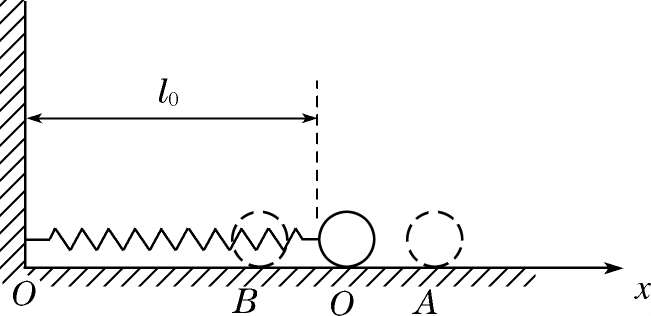
图4-1 弹簧振子的运动
从上面的分析可以知道,弹簧的弹性恢复力和惯性是小球产生往复运动(即振动)的关键.现在我们来讨论弹簧振子的运动方程.在图4-1中,设小球在 x 轴方向上运动,坐标原点在平衡位置 O 点,则弹簧的弹性恢复力为

由牛顿第二定律可以得到小球的运动微分方程为
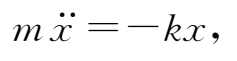
或写为标准形式为

式中

称为简谐振动的 圆频率 (或 角频率 ),它由振动系统的特性所决定,是系统的固有属性.
运动微分方程(4.2)式的通解为正弦或余弦函数:

其中
A
和
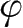 为两个待定常数.将(4.4)式对时间求导,可以得到小球的速度
v
x
和加速度
a
x
为
为两个待定常数.将(4.4)式对时间求导,可以得到小球的速度
v
x
和加速度
a
x
为
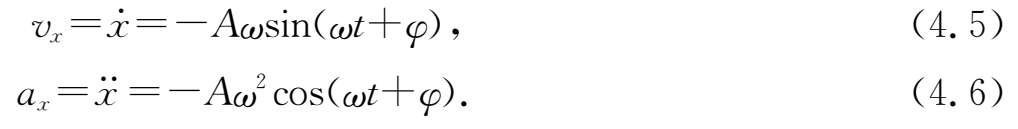
可见,对于做简谐振动的物体,它的坐标、速度和加速度随时间的变化都呈余弦或正弦函数关系.可以定义速度振幅和加速度振幅分别为

由(4.4)式和(4.6)式可以马上得到(4.2)式:

即加速度与位移成正比,且与位移方向相反.(4.2)式或(4.8)式是物体做简谐振动的本质特征.只要物体运动的动力学方程可以写成(4.2)或(4.8)式的形式,物体就一定是做简谐振动.
由简谐振动的三角函数解(4.4)~(4.6)式可以知道,物体的位置、速度和加速度都是时间的周期函数.由于余弦函数的周期为2π,故简谐振动的 周期 T 满足 ω T =2π,即

对于弹簧振子,考虑(4.3)式圆频率的表示形式,有

对于常见的另一种简谐振动形式——单摆,它的振动周期为

式中 l 为单摆的摆长, g 为重力加速度.
频率 ν 是1秒时间内重复振动的次数,故有

其SI单位为Hz.1Hz表示1秒内物体完成一次重复振动.显然,根据(4.9)式,有

上式表示圆频率与频率只相差一个常数2π,故它们在本质上反映同一物理量,只是使用环境有所不同而已.简谐振动的运动方程也可以用周期和频率写为
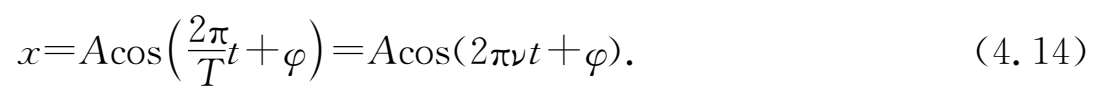
圆频率(频率、周期)由描述系统固有特征的一些物理量决定.对于弹簧振子,这些物理量是质量和弹性系数,其中质量是振动系统惯性的反映,而弹性系数是系统所受线性回复力的反映.对于单摆,它取决于摆球和地球之间的万有引力,此时的系统由摆球和地球构成,而表征这个系统特征的量是摆长和重力加速度.由于引力的特性是引力质量与惯性质量相等,故在(4.11)式中,二者消去了从而不出现.
运动方程(4.4)式中除圆频率由系统固有特征所确定外,还有两个待定常数.其中正数 A 是物体偏离平衡位置的最大位移,称为 振幅 .对于一些非机械运动的简谐振动,其振幅不是长度量,故 A 可以具有其他的量纲.
物体在做简谐振动时,当振幅
A
和圆频率
ω
给定,则振动物体在任一时刻相对平衡位置的位置、速度和加速度都由物理量(
ω
t
+
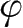 )决定.物理量(
ω
t
+
)决定.物理量(
ω
t
+
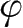 )称为简谐振动的
相位
,又称
位相
.对于图4-1所示弹簧振子,根据(4.4)式和(4.5)式,当相位(
ω
t
1
+
)称为简谐振动的
相位
,又称
位相
.对于图4-1所示弹簧振子,根据(4.4)式和(4.5)式,当相位(
ω
t
1
+
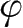 )=π/2时,有
x
=0,
v
x
=-
A
ω
,即在
t
=
t
1
时刻,物体在平衡位置,并以速度
v
x
=-
A
ω
向左运动.当(
ω
t
2
+
)=π/2时,有
x
=0,
v
x
=-
A
ω
,即在
t
=
t
1
时刻,物体在平衡位置,并以速度
v
x
=-
A
ω
向左运动.当(
ω
t
2
+
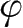 )=3π/2时,有
x
=0,
v
x
=
A
ω
,即在
t
=
t
2
时刻,物体仍在平衡位置,但以速度
v
x
=
A
ω
向右运动.这说明在
t
1
和
t
2
两个不同时刻,由于相位的不同,物体的运动状态也不相同.相位是一个重要的概念,它反映了物体振动状态的一种顺序变化.在研究波动、物理光学、无线电技术、交流电等问题时,相位都起着关键性的作用.
)=3π/2时,有
x
=0,
v
x
=
A
ω
,即在
t
=
t
2
时刻,物体仍在平衡位置,但以速度
v
x
=
A
ω
向右运动.这说明在
t
1
和
t
2
两个不同时刻,由于相位的不同,物体的运动状态也不相同.相位是一个重要的概念,它反映了物体振动状态的一种顺序变化.在研究波动、物理光学、无线电技术、交流电等问题时,相位都起着关键性的作用.
在相位的表示式(
ω
t
+
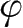 )中,
)中,
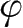 为
t
=0时的相位,称为
初相位
,表示初始时物体的运动状态.由于相位可以相差2π,故通常限制
为
t
=0时的相位,称为
初相位
,表示初始时物体的运动状态.由于相位可以相差2π,故通常限制
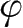 在[0,2π)或(-π,π]范围内取值.振动的振幅和初相位可以由初始条件确定.设初位置和初速度已知:
t
=0时
x
=
x
0
,
v
x
=
v
x
0
,将此初始条件代入(4.4)式和(4.5)式得
在[0,2π)或(-π,π]范围内取值.振动的振幅和初相位可以由初始条件确定.设初位置和初速度已知:
t
=0时
x
=
x
0
,
v
x
=
v
x
0
,将此初始条件代入(4.4)式和(4.5)式得
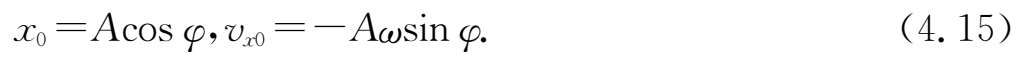
由此容易解得振幅为

而初相位满足

利用初始条件求初相位时要注意,单独(4.17)式不能完全确定
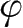 ,还需根据(4.15)式选择两个可能值中的一个.
,还需根据(4.15)式选择两个可能值中的一个.
例4.1
某物体在做圆频率
ω
=5 rad/s的简谐振动,初始条件为
t
=0时,
x
0
=1m,
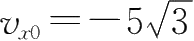 m/s,求物体振动的振幅和初相位.
m/s,求物体振动的振幅和初相位.
解: 由(4.16)式得
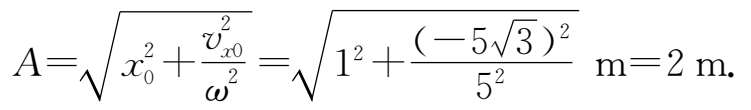
由(4.17)式得到
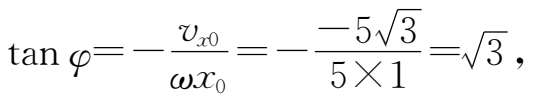
故
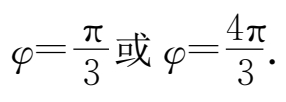
又由(4.15)式得到
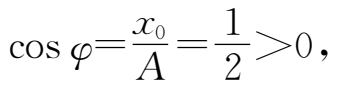
故
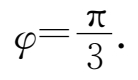
例4.2 已知物体做简谐振动时,最大位移为10cm.开始振动时,物体处于-5cm的位置,且向正方向运动,而当 t =1s时,物体第一次处于5cm处.试写出物体的振动方程.
解: 设物体的运动方程为
x
=
A
cos(
ω
t
+
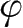 ).
).
代入初始条件得
-5=10cos
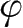 ,
,
即
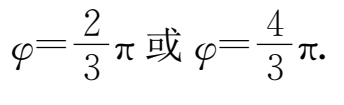
因为
v
x
0
=-
A
ω
sin
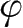 >0,
>0,
故
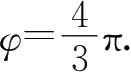 于是
于是
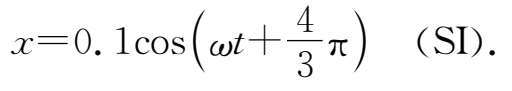
再由 t =1s时 x =5cm的条件,得
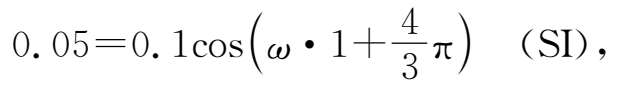
即
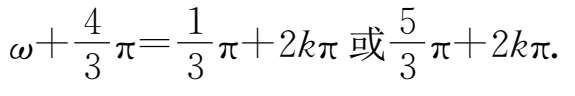
而由于此时物体是第一次处于5cm处,故 T >1s,且
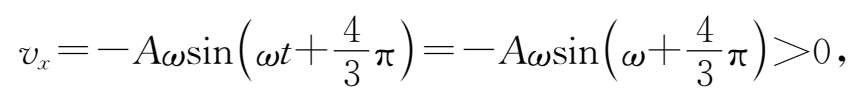
于是
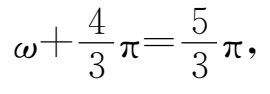
即
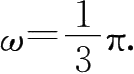 最后有
最后有
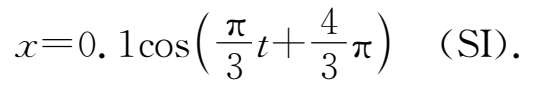
简谐振动位置和时间的函数关系还可以用旋转矢量的方法来表示.使用旋转矢量法的好处是可以直观清楚地给出简谐振动的各特征量(振幅、圆频率、相位)以及它们之间的关系.
如图4-2所示,从直角坐标系
O
-
xy
的原点
O
出发,作一矢量
A
,令
A
的模等于振动的振幅
A
.矢量
A
逆时针匀速转动,其角速度就是圆频率
ω
,且在初始时刻与坐标横轴
x
的夹角就是初相位
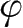 .由圆周运动可知,在任意一个时刻
t
,矢量
A
与
x
轴的夹角为
ω
t
+
.由圆周运动可知,在任意一个时刻
t
,矢量
A
与
x
轴的夹角为
ω
t
+
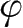 ,而它在
x
轴上的投影为
,而它在
x
轴上的投影为
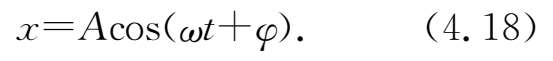
此式说明, 这样特意构造出的旋转矢量,其端点在 x 轴上投影就正好做(4.4)式所示的简谐振动! 于是,对于简谐振动,我们找到了一个很好、很直观的几何解释.而振动物体的速度和加速度可以从该矢量端点速度和加速度的 x 轴分量得到.
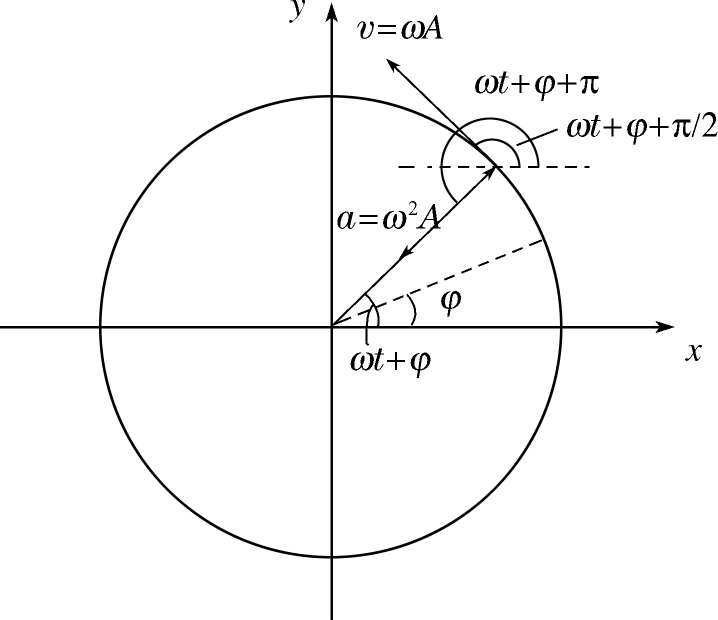
图4-2 旋转矢量图
由图4-2可以得到,矢量
A
的矢端速度沿切线方向,大小为
v
m
=
ω
A
,方向为与
x
轴呈夹角
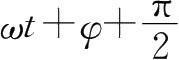 ,故它在
x
轴上的投影为
,故它在
x
轴上的投影为
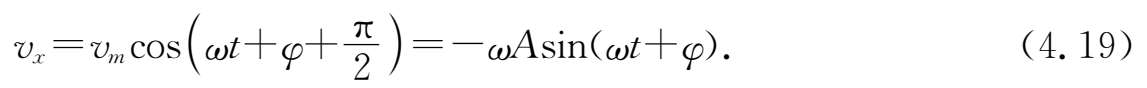
而矢量
A
的矢端的加速度就是向心加速度,其大小为
a
m
=
ω
2
A
,方向指向坐标系原点
O
点,与
x
轴的夹角为
ω
t
+
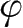 +π,故它在
x
轴上的投影为
+π,故它在
x
轴上的投影为
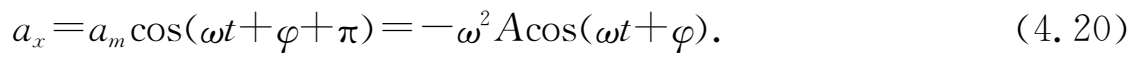
(4.18)~(4.20)式正是前面得到的简谐振动的位移、速度和加速度公式(4.4)~(4.6)式.
由此可以知道,以圆频率
ω
为角速度、以振幅
A
为模、以初相位
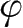 为初始夹角的旋转矢量
A
,其端点的
x
轴投影的运动完全
模拟
了一个具有上述参数的简谐振动.这种用旋转矢量在坐标轴上的投影来描述简谐振动的方法称为简谐振动的
旋转矢量法
.
为初始夹角的旋转矢量
A
,其端点的
x
轴投影的运动完全
模拟
了一个具有上述参数的简谐振动.这种用旋转矢量在坐标轴上的投影来描述简谐振动的方法称为简谐振动的
旋转矢量法
.
使用旋转矢量法可以方便地得到结果.在上面的例4.2中,根据题意,相应的过程用旋转矢量表示的话只能是图4-3中的
BC
段.于是易得初相位
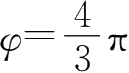 ,且圆频率(即角速度)
,且圆频率(即角速度)

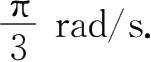 可见,利用旋转矢量法可以极大地简化计算.
可见,利用旋转矢量法可以极大地简化计算.
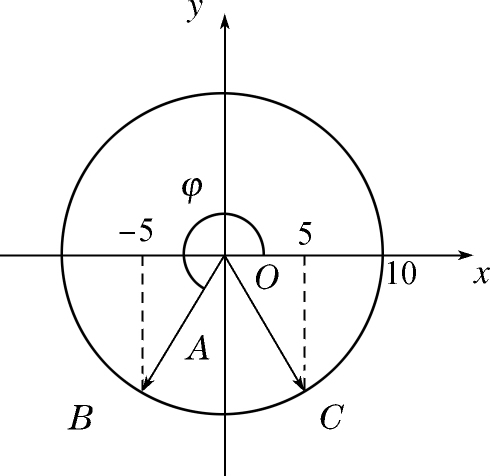
图4-3 用旋转矢量法解例4.2
但需要说明的是,旋转矢量法仅仅是为了更好地理解、更直观地描述简谐振动而引进的一种工具,矢量 A 本身并不做简谐振动;做简谐振动的是 A 的端点的投影.