




根据角动量定理,如果力矩为0,那么体系的角动量将保持不变.这就是角动量守恒定律.根据情况的不同,角动量守恒定律有多种形式.质点和质点系的情况前面已经阐述,下面专门讨论刚体情况.
刚体的对轴角动量由(3.19)式给出,它正比于对轴转动惯量和角速度的乘积.由转动定理(即对轴角动量定理)(3.20)式可知,当外力对轴的总力矩为零时,刚体对该轴的角动量保持不变.故在定轴转动中,当 M z =0时,有

由于刚体的对轴转动惯量是不变的,故

在航海、航空、航天以及导弹中使用的定向装置回转仪,其基本原理就是刚体的角动量守恒定律.这种回转仪高速旋转,而且尽量把外力矩减到了最小.虽然回转仪没有可以看见的转轴,但它靠惯性而保持着其转轴方向和转动角速度大小不变,因为这分别表征着其角动量的方向和大小.因此,不管飞行器如何飞行,回转仪总是指向确定方向,从而可以用于定向.
根据质点系的对轴角动量定理(3.16)式,如果合外力矩的 z 分量 M z =0,那么质点系的对轴角动量将守恒.在实际使用中经常碰到整个体系不能视为一个刚体的情况,但体系的始末状态都表现为一些刚体(和质点)的组合.此时,刚体的对轴角动量根据(3.19)式是很容易计算的,于是可以得到有用的方程.
例如,对于一个可以形变的物体,虽然其转动惯量可以变化,但(3.27)式可以适用,只要物体的始末状态都可以视为刚体.这意味着转动惯量 I 和角速度 ω 都可以改变,但它们的乘积将保持不变.因此,当转动惯量增大时,角速度必然减小;当转动惯量减小时,则角速度必然增大.
这样的实例有很多.例如,体操运动员在做翻转动作时,通常在起跳后将身体蜷缩起来,以减小转动惯量,从而增加转动的角速度,使得翻转的次数尽量得多.当运动员准备落地时,又会将身体展开,以增大转动惯量而减小角速度,便于稳定地落地.溜冰运动员和舞蹈演员在做旋转动作时,通过张开或收缩手臂来改变转动的快慢,其原理也是利用改变转动惯量来控制转动.在工业生产中,离心式调速器也是通过角动量守恒的原理来调节转速.
例3.3 工业上常将两个飞轮用摩擦啮合器使它们以相同的转速一起转动.它的基本结构是两飞轮的轴杆在同一中心线上,转动惯量分别为 I 1 =20kg·m 2 和 I 2 =40kg·m 2 .初始时,第一个飞轮的转速为 n 1 =500r/min,另一个为静止.试求两轮啮合后的共同转速.
解: 考虑两飞轮组成的一个系统,则系统不受外力矩,啮合前后的角动量守恒.设啮合后的角速度为 ω ,有
I 1 ω 1 + I 2 ω 2 =( I 1 + I 2 ) ω ,
或
I 1 n 1 + I 2 n 2 =( I 1 + I 2 ) n ,
故
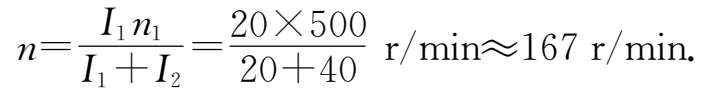
例3.4 质量为 M ,半径为 R 的水平均匀圆盘可以绕竖直轴转动.在盘的边缘上有一个质量为 m 的人,二者开始都相对地面静止.当人沿盘的边缘相对于圆盘走一周时,盘对地面转过的角度为多少?略去转轴处的摩擦阻力.
解: 人和盘组成的系统中,外力矩在转轴上的分量为零,满足角动量守恒.人和盘对转轴的转动惯量分别为 I 1 = mR 2 和 I 2 = MR 2 /2.设二者的角速度分别为 ω 1 和 ω 2 ,角位移分别为 θ 1 和 θ 1 ,由角动量守恒,有
I 1 ω 1 - I 2 ω 2 =0.
故
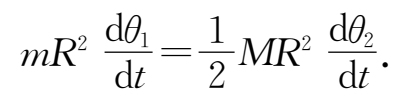
两边同乘以d θ ,并积分,有
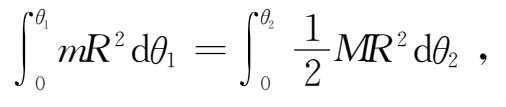
即
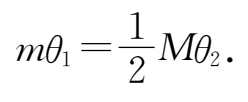
又因为人在盘上走一周,满足
θ 1 + θ 2 =2π.
故
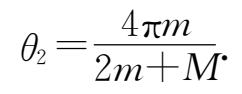
例3.5 如图3-7所示,质量为2.97kg、长为1.0m的均匀细杆可绕水平且光滑的 O 轴转动,杆静止于竖直方向.一质量为10g的粒子以水平速度200m/s射向杆的下端,并未穿出,而是和杆一起运动.求碰撞前后系统的动能改变和动量改变.
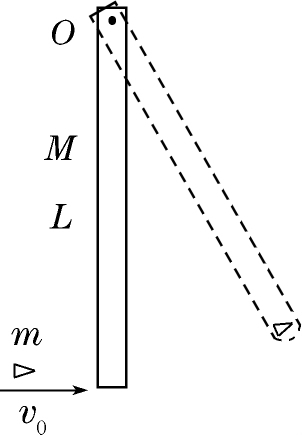
图3-7 粒子入射细杆
解: 碰撞过程动量并不守恒,因为 O 处的约束会施予杆以额外的力,使得 O 点不动.但系统对 O 点的角动量守恒:
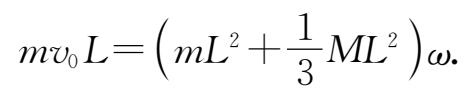
于是
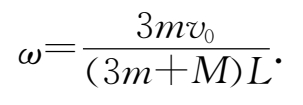
动能改变为
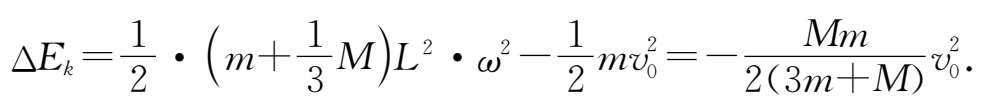
刚体的动量等于把质量集中于质心时的动量,故动量改变为
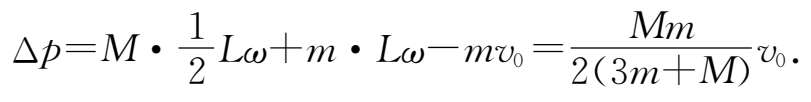
可见,系统的动能有损失,但动量有增加.后者是因为,若 O 点不被固定,则碰撞后的瞬间 O 点将向后运动.因此,碰撞时 O 处的约束施予杆的力是向前的,使总动量增加.