




动量定理阐明了力的时间积累跟物体运动状态改变的关系,那么力的空间积累呢?考虑一个质点,根据牛顿第二定律,有
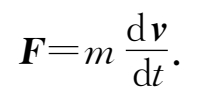
上式两边点乘位移d r = v d t ,得
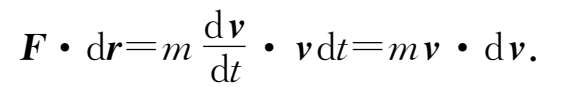
下面计算 v ·d v .根据点积的定义,
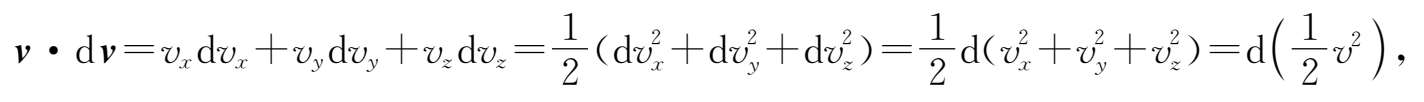
故

这是一个非常紧凑的公式.左边表示力的空间积累,右边是一个状态量的全微分.我们定义:左边的

称为
功(元功)
[1]
,右边的
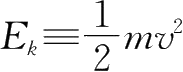 称为
动能
,则(2.13)式表明,外力所做的功等于物体动能的增量.
称为
动能
,则(2.13)式表明,外力所做的功等于物体动能的增量.
把(2.13)式两边积分,得到
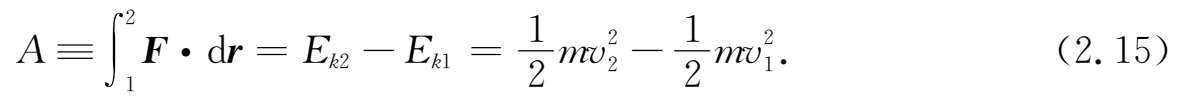
这是动能定理的有限形式.
可以看出,动能也是对物体运动状态的一种描述.力能够改变物体的运动状态,也就能够改变物体的动能,只是这种改变是通过 力的空间积累 ——功来实现的.所以,动能定理也是对力学的根本问题——力与运动的关系的定量回答.
功是力的空间积累效应,是一个非常重要的物理量,同时又比冲量要复杂.因此,有必要专门讨论一下功的概念.
考虑一个无限小过程,如图2-3所示.在此过程中,力所做的功由(2.14)式给出:

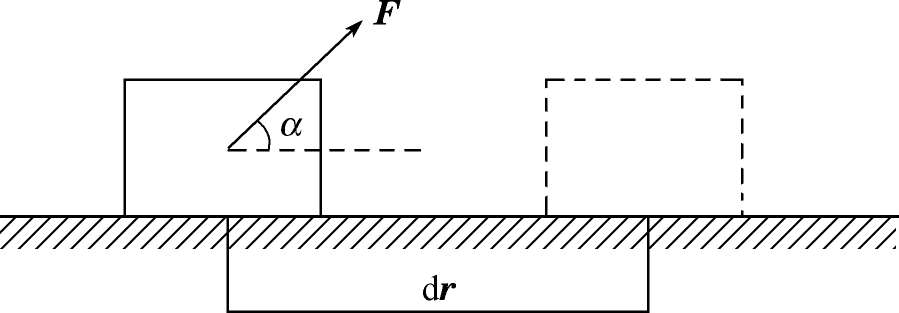
图2-3 力所做的功
该式可以做两种等价的理解:(1)力在位移方向的分量与位移的乘积;(2)位移在力方向上的分量与力的乘积.
功是一个标量,它没有方向,但有大小和正负,是一个代数量.功的正负由角
α
决定.当0≤
α
<
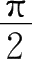 时,
时,
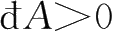 ,力对物体做正功;当
α
=
,力对物体做正功;当
α
=
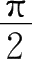 时,
时,
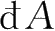 =0,力对物体不做功;当
=0,力对物体不做功;当
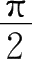 <
α
≤π时,
<
α
≤π时,
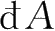 <0,力对物体做负功.此时,我们也说,物体克服阻力做负功.
<0,力对物体做负功.此时,我们也说,物体克服阻力做负功.
对于一个一般的过程,如图2-4所示,物体沿曲线运动从 a 点到达 b 点,沿这一路径力 F 做的功,可以通过对(2.16)式积分得到
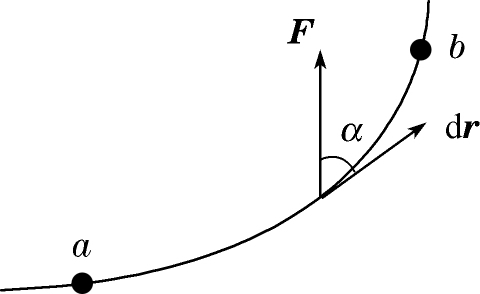
图2-4 力沿曲线做的功
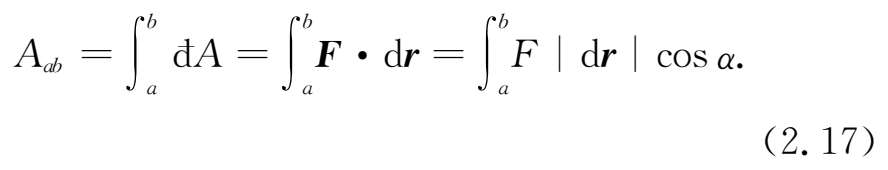
如果物体在一组力 F i 的作用下,沿曲线从 a 点到达 b 点,则合力 F 对物体做的功为
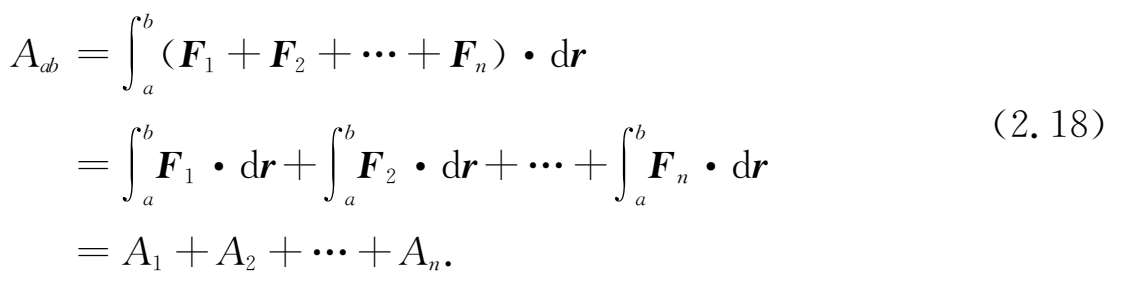
上式说明,合力所做的功等于各分力沿同一条路径所做的功的代数和.在SI国际单位制中,功的单位是焦耳,用J表示.
在直角坐标系中,力和元位移可以表示为
F = F x i + F y j + F z k ,d r =d x i +d y j +d z k ,
这样,(2.17)式就可以写为
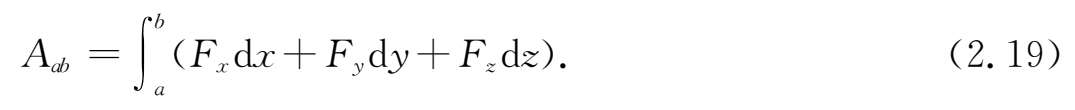
力在单位时间内所做的功称为功率.设力
F
在Δ
t
时间内做的功为Δ
A
,则在Δ
t
时间内的平均功率为
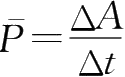 .当Δ
t
趋于零时,可得瞬时功率为
.当Δ
t
趋于零时,可得瞬时功率为

将功的表示式(2.16)式代入,有

也就是说,力的瞬时功率等于力和速度的点积.在SI国际单位制中,功率的单位是瓦特,用W表示.
功的数值一般与路径有关.在(2.17)式和(2.19)式中的积分标明了始末位置,但原则上还必须标明积分路径.但人们发现,有一类力所做功的大小仅与物体的始末位置有关,而与物体所经历的路径无关,这类力称为 保守力 .比较常见的保守力有重力、万有引力、弹性力等.下面分别给出它们的功.
重力是最简单的保守力.设质点的质量为 m ,在重力作用下沿任意路径由 a 点运动到 b 点.在地球表面附近,重力的大小不变,方向竖直向下.选择地面为坐标原点, z 轴垂直于地面向上,则重力只有 z 方向的分量 G z =- mg .代入(2.19)式,有
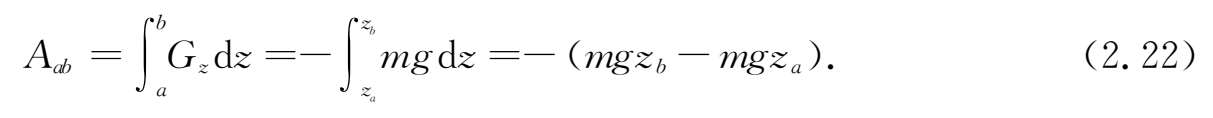
上式表明,重力的功只与质点的始末位置有关(而且只取决于始末高度),与所走过的路径无关.
对于万有引力,如图2-5所示,质量为 M 的质点保持静止在原点,质量为 m 的质点在 M 施与的万有引力作用下做曲线运动.设质点 m 相对于 M 的初末位置分别为 r a 和 r b ,则根据万有引力公式(2.3)式,有
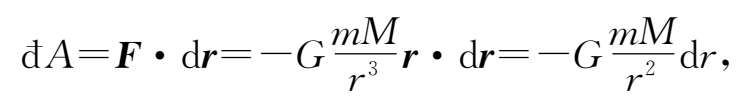
其中 r ·d r = r d r (在图中,d r 沿径向的分量就是d r .也可参见(2.13)式的推导过程).上式表明,万有引力做功只取决于半径的变化,与垂直于半径方向的运动无关.于是
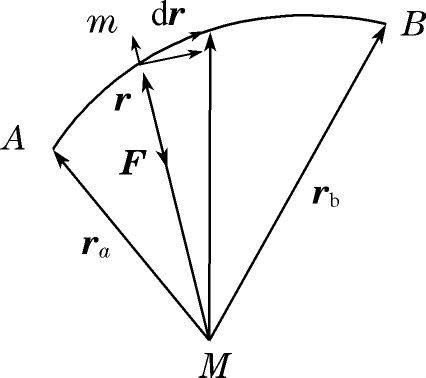
图2-5 万有引力做的功
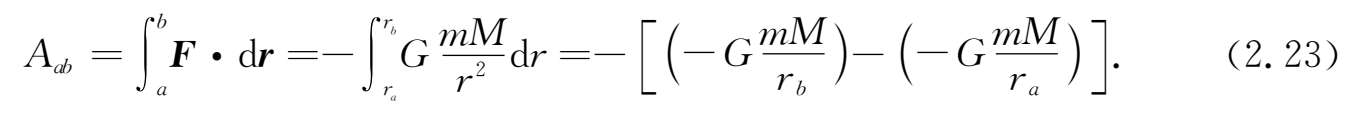
式(2.23)表明引力的功也只由质点的始末位置决定(而且只决定于始末距离),与所走过的路径无关.
弹性力满足胡克定律(2.4)式.考虑弹簧在 x 轴方向上伸缩,选择一维坐标的坐标原点在弹簧的自然长度处,有
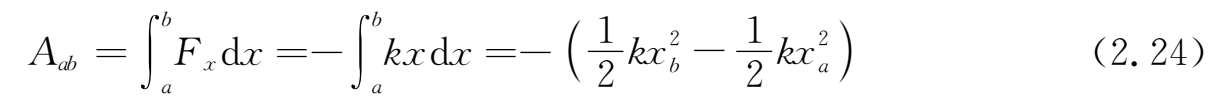
显然,弹性力做的功也只由质点的始末位置决定.
上述各力做功的结果显示, 保守力做功仅由物体的始末位置决定,而与中间路径无关 .由此马上得到, 保守力沿任意一条闭合路径做功之和为零 ,即

这是因为起点与终点重合了.(2.25)式也可以视为保守力的定义.
与此相反,摩擦力做功就不满足此性质.以在粗糙水平面上运动的质点为例,由于滑动摩擦力始终跟运动方向相反,故滑动摩擦力始终做负功.它沿闭合路径做功之和就只能为负数,不可能等于0.而且,它做的功显然跟路径有关:对于相同的始末位置,路程越长,滑动摩擦力做的负功越多.因此,摩擦力不是保守力.
例2.4 质点在 xy 平面内受外力 F =2 xy i + x 2 j (SI)的作用,求质点沿如下不同路径从点 O (0,0)运动到点 A (1,1)的过程中,力 F 所做的功:
(1)路径 L 1 :先沿 x 轴从 O 点运动到点 B (1,0),再平行于 y 轴运动到 A 点;
(2)路径 L 2 :沿直线 y = x 从 O 点到 A 点.
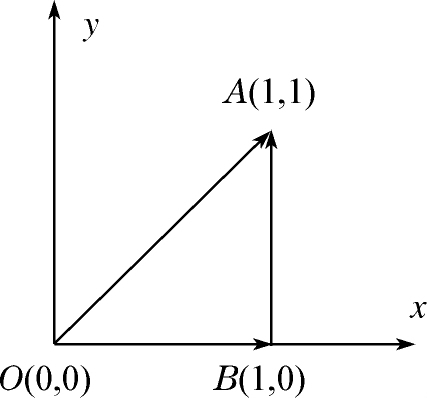
图2-6 例2.4题图
解:
(1)
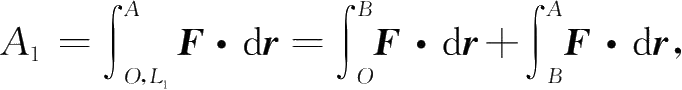
其中对于路径 OB , y =0,d y =0,故
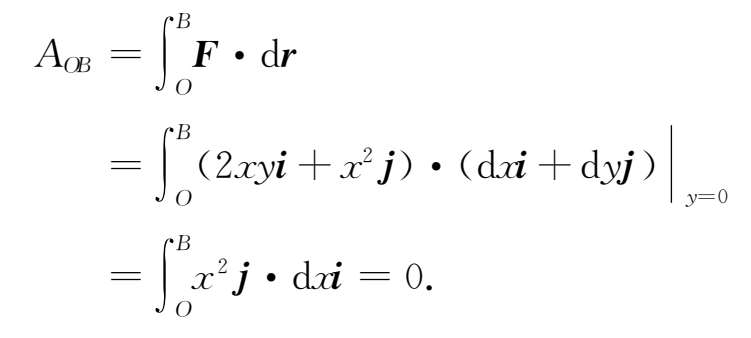
对于路径 BA , x =1,d x =0,故
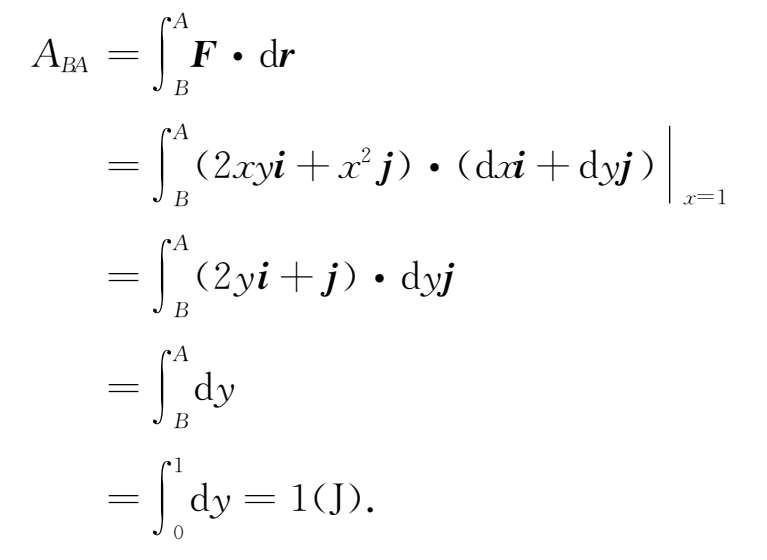
故
A 1 = A OB + A BA =1J.
(2)对于直线 OA ,有 y = x ,故
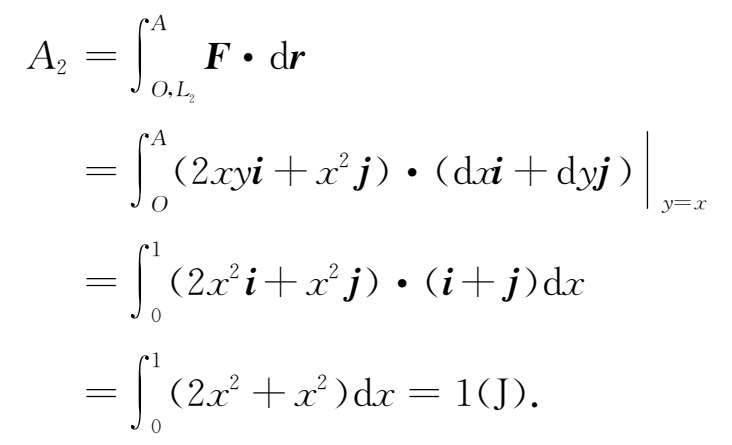
可以看出,尽管积分路径不同,但积分结果完全相同.我们还可以证明,沿其他任意路径得积分结果都是这个数值,从而说明该力为保守力.事实上,考虑题中所给的力在一般情况下的元功:
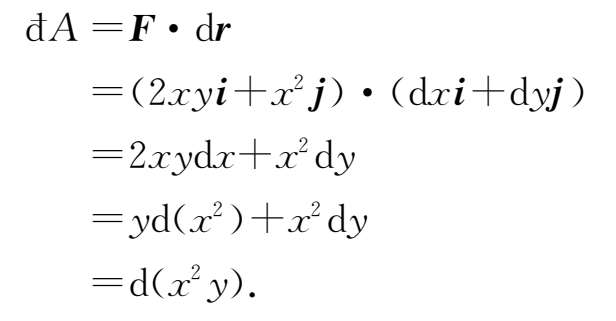
可见,该力所做的功必然等于函数 x 2 y 在终点和起点的函数值差,这当然跟路径无关.
[1]
功是过程量,故在无限小过程中的元功用
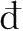 表示,以区别于函数(状态量)的全微分符号d,因为
表示,以区别于函数(状态量)的全微分符号d,因为
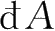 一般不是某个量
A
的微分(详见第13章),只在特殊情况(即保守力)时才能如此.
一般不是某个量
A
的微分(详见第13章),只在特殊情况(即保守力)时才能如此.