




摄氏温度 (Celsius,C)的由来是在标准大气压环境,水的凝固点是0℃、沸点是100℃,中间划分100等份,每个等份是1℃。这样命名是为了纪念瑞典科学家 安德斯·摄尔修斯 (Anders Celsius)。
华氏温度 (Fahrenheit,F)的由来是在标准大气压环境,水的凝固点是32℉、水的沸点是212℉,中间划分180等份,每个等份是1℉。这是为了纪念德国科学家 丹尼尔·加布里埃尔·华伦海特 (Daniel Gabriel Fahrenheit)。
摄氏 和 华氏 温度互转的公式如下:
摄氏 温度 = ( 华氏 温度 – 32 ) * 5 / 9 华氏 温度 = 摄氏 温度 * ( 9 / 5 ) + 32
程序实例ch4_28.py: 请输入华氏温度,这个程序会输出摄氏温度。

执行结果

假设已知条件是:
· 贷款金额 :笔者使用loan当变量
· 贷款年限 :笔者使用year当变量
· 年利率 :笔者使用rate当变量
然后我们需要利用上述条件计算下列结果:
· 每月还款金额 :笔者用monthlyPay当变量
· 总共还款金额 :笔者用totalPay当变量
处理这个贷款问题的数学公式如下:

银行的习惯是用年利率,所以碰上这类问题我们需要将所输入的利率先除以100,这是转成百分比,同时要除以12表示是月利率。可以用下列方式计算月利率,笔者用monthrate当变量。
monthrate = rate / (12*100) # 第5行
为了不让求每月还款金额的数学式变得复杂,笔者将分子(第8行)与分母(第9行)分开计算,第10行则是计算每月还款金额,第11行是计算总共还款金额。
程序实例ch4_29.py: 根据已知条件计算还款金额。

执行结果

假设正五角形边长是s,其面积的计算公式如下:
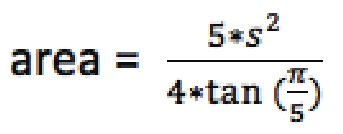
上述计算正五角形面积需要使用数学的PI(π)和tan( ),虽然我们可以使用3.14159代替,不过笔者此处先引导读者学习使用Python的数学模块,可以使用import math导入此数学模块。
程序实例ch4_30.py: 请输入正五角形的边长s,此程序会计算此正五角形的面积。

执行结果

我们可以将上述概念扩充应用在正多边形面积计算中。
math 是标准函数库模块,由于没有内置在Python直译器内,所以使用前需要导入此模块,导入方式是使用 import ,可以参考语法: import math。
导入模块后,可以在Python的IDLE环境使用dir(math)了解此模块提供的 属性 或 函数 (或称 方法 )。

下列是常用的math模块的 属性 与 函数 :
· pi :PI值(3.14152653589753),直接设定值称 属性 。
· e :e值(2.718281828459045),直接设定值称 属性 。
· inf :极大值,直接设定值称 属性 。
· ceil(x) :回传大于x的最小整数,例如,ceil(3.5) = 4。
· floor(x) :回传小于x的最大整数,例如,floor(3.9) = 3。
· trunc(x) :删除小数位数。例如,trunc(3.5) = 3。
· pow(x,y) :可以计算x的y次方,相当于x**y。例如,pow(2,3) = 8.0。
· sqrt(x) :开根号,相当于x**0.5,例如,sqrt(4) = 2.0。
· radians( ) :将 角度 转成 弧度 ,常用在三角函数中。
· degrees( ) :将 弧度 转成 角度 。
· 三角函数: sin( ) 、 cos( ) 、 tan( )等, 参数是 弧度 。
· 不同底的对数函数: log( ) 、 log10( ) 、 log2( ) 等。
在使用上述math模块时,必须在前面加math,例如: math.p i或 math.ceil(3.5) 等,此概念应用在上述所有模块的函数操作。有了上述概念就可以进入本节的主题了。
地球是圆的,我们可以使用经度和纬度了解地球上每一个点的位置。有了2个地点的经纬度后,可以使用下列公式计算彼此的距离。
distance = r*acos(sin(x1)*sin(x2)+cos(x1)*cos(x2)*cos(y1-y2))
上述 r 是地球的半径,约 6371 千米,由于Python的三角函数 参数 皆是 弧度 (radians),我们使用上述公式时,须使用math.radian( )函数将 经纬度角度 转成 弧度 。上述公式 西经 和 北纬 是 正值 , 东经 和 南纬 是 负值 。
经度坐标为-180° ~ 180° , 纬度坐标为-90° ~ 90° ,虽然我们习惯称经纬度,在用小括号表达时却是( 纬度 , 经度 ),也就是第一个参数是 纬度 ,第二个参数是 经度 。
获得经纬度最简单的方式是开启Google地图,开启后就可以看到我们目前所在地点的经纬度,点选其他地点就可以看到所选地点的经纬度信息。
程序实例ch4_31.py: 香港红磡车站的经纬度是(22.2839, 114.1731),台北车站的经纬度是(25.0452, 121.5168),请计算台北车站至香港红磡车站的距离。

执行结果

“今有鸡兔同笼,上有三十五头,下有百足,问鸡兔各几何?”这是古代的数学问题,表示一个笼子里有35个头、100只脚,然后问笼子里面有几只鸡与几只兔子。鸡有1个头、2只脚,兔子有1个头、4只脚。我们可以使用基础数学解此题目,也可以使用循环解此题目,这一小节笔者将使用基础数学的联立方程式解此问题。
如果使用基础数学,x代表chicken,y代表rabbit,可以用下列公式推导。

经过推导可以得到下列结果:
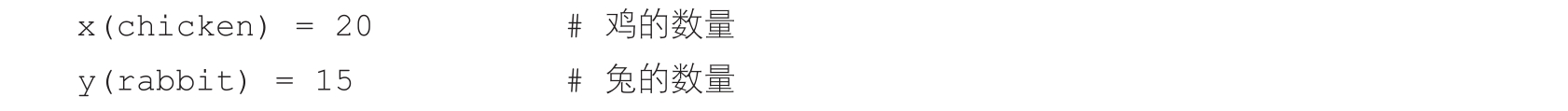
假设f是脚的数量,h代表头的数量,可以得到下列公式:
x(chicken) = f / 2 – h
y(rabbit) = 2h – f / 2
程序实例ch4_32.py: 请输入头和脚的数量,本程序会输出鸡的数量和兔的数量。

执行结果

注 并不是每个输入皆可以获得解答,必须是合理的数字。
约翰·卡尔·弗里德里希·高斯(Johann Karl Friedrich Gauss,1777—1855)是德国数学家。他在9岁时就发明了等差数列求和的计算技巧,在很短的时间内计算了1~100的整数和。使用的方法是将第1个数字与最后1个数字相加得到101,将第2个数字与倒数第2个数字相加得到101,然后依此类推,可以得到50个101,然后执行50 * 101,最后得到解答。
程序实例ch4_33.py: 使用等差数列计算1~100的总和。

执行结果
