




甲乙两个人为一件事发生了争执,他们来到寺院让一个德高望重的老和尚评理。甲来到老和尚面前说了自己的一番道理,老和尚听后说:“你说得对。”接着,乙来到老和尚面前说了和甲的意见相反的另一番道理,老和尚听后说:“你说得对。”站在一旁的小和尚说:“师父,怎么两个人说的都对呢?要么甲对乙错,要么乙对甲错。”老和尚说:“你说得对。”
也许你觉得老和尚的话自相矛盾,但是真的存在绝对的对与错吗?很多事并非只有一种解释。从甲与这件事的关系来看,甲说的是对的;从乙与这件事的关系来看,乙说的是对的;从小和尚与这件事的关系来看,小和尚说的也是对的。
我们所处的这个世界是一个多元的、复杂的世界,我们所做的每一件事都有利有弊,对与错、好与坏就像一股黑线和一股白线相互交织,有时甚至紧密得难以分开。我们在观察和解释事物的时候,应该避免单一和僵化的解释,那样只会导致偏执一词、钻牛角尖,看不到事情的全貌。
要想在这个世界上从容地生存发展,就要运用关系发散法来思考问题,即从宏观的角度充分分析事物所处的复杂关系,并从中寻找相应的思路,得出客观全面的结论。人们常用“八面玲珑”来形容那些善于为人处事的人,这个词形象地体现了关系发散法的好处。
关系发散的另外一层意思是从另一个角度重新理解和解释事物之间的关系。很多时候我们习惯了事物之间的某种关系,于是把这种关系看做是亘古不变的,从来不试图改变。事实上,只要你愿意,完全可以对事物的关系做出另一番解释。
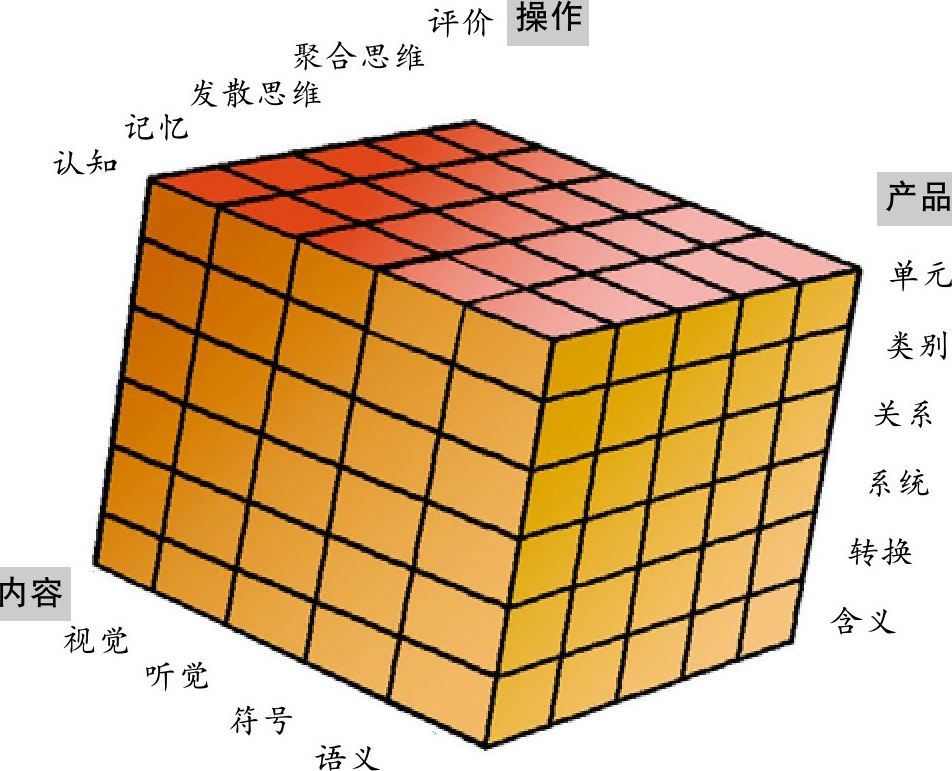
■智力的三维结构模型
古时候,有一位秀才进京赶考,住进了一家客店。考试前一天他做了3个梦:在第一个梦里,他在墙上种白菜;在第二个梦里,他在下雨天戴了斗笠还打伞;在第三个梦里,他跟心爱的表妹脱光了衣服背靠着背躺在一起。
秀才觉得这3个梦似乎意味着什么,于是去找算命先生解梦。算命先生听了他的描述后连连摇头说:“你还是回家吧!你想想,高墙上种菜不是白费劲吗?戴斗笠打雨伞不是多此一举吗?跟表妹脱光了躺在一张床上了,却背靠背,不是没戏吗?”秀才听后觉得有道理,没心思考试了,回到客店收拾包袱准备回家。店老板觉得非常奇怪,问:“不是明天才考试吗,你怎么今天就回乡了?”
秀才把解梦的事告诉了店老板,店老板听后笑了起来:“我也会解梦的。我倒觉得,你这次一定要留下来。你想想,墙上种菜不是高中(种)吗?戴斗笠打伞不是说明你这次有备无患吗?跟你表妹脱光了背靠背躺在床上,不是说明你翻身的时候就要到了吗?”
秀才听后觉得更有道理,于是信心十足地参加了考试,结果中了探花。
在生活中,我们同样需要从不同的角度来解释两件事之间的关系。“塞翁失马,焉知非福”就是对关系发散的运用。“福兮祸之所倚,祸兮福之所伏”,丢了一匹马,并不仅仅给塞翁造成损失,有可能还会带来好处,虽然那好处没立刻显现出来,但是通过关系发散法塞翁预测到了可能的好处。
此外,关系发散法在数学题中的应用也很广泛。
在一节思维培训课上,一个小学一年级的数学教师向思维培训师请教如何教孩子们练习发散思维。思维培训师在黑板上写了一道算术题:
2+3=?
然后,他说:“这是小学一年级常见的计算题,只有唯一的答案,对就是对,错就是错。这会让孩子们养成寻找一个答案的思维习惯,导致思维的扁平化,遇到问题时缺乏寻找多种答案的意识和能力。虽然大部分数学题是一题一解的,但是我们可以运用关系发散法来改变出题的方式。”接着,他在黑板上写下了这道题:
5=?+?
那个数学老师一下子醒悟过来,显然学生在计算这道题的时候思维是发散的,而计算前一道题的时候思维却是封闭的。
思维培训师对等式两边的关系进行了发散处理,把已知变未知,把未知变已知,从由分求和到由和求分。有人把这种发散方法称为“分合发散”。曹冲称象的方法就是对分合发散的运用。
三国时,孙权送给曹操一头大象。曹操很高兴,问他的谋士们:“谁有办法称一称它的重量?”有人说造一个巨型的秤,有人说把大象宰了切成块。这时曹冲说:“我有办法。”他让众人跟他来到河边,叫人把大象牵到一条大船上,等船身稳定了,在船舷上齐水面的地方刻了一条线做标记。然后,他让人把大象牵到岸上,把岸边的石头一块一块地往船上装,船身就一点儿一点儿往下沉。等船身沉到刻的那条线时,曹冲就叫人停止装石头。接下来,大家都知道怎么办了吧?称一称船上石头的就知道大象有多重了。
在这个例子中曹冲巧妙地把大象和石头联系起来,把难于称量的大象的重量分解为容易称的石头的重量,使问题迎刃而解。与此类似的还有西汉时期的孙宝称馓子的故事。
一个农夫撞倒了卖馓子的小贩,馓子掉在地上全摔碎了。农夫愿意赔偿50个馓子的价钱,但是小贩坚持说他有300个馓子,二人僵持不下。这时,担任京兆尹的孙宝路过,他让人把地上的碎馓子收集起来称出重量,然后买来一个馓子称出一个馓子的重量,两数相除计算出馓子的个数。农夫和小贩都心服口服,农夫按照馓子的数目赔钱给了小贩。
这同样是对关系发散法的应用,孙宝同时考虑了整体与个体,数量与重量的关系。馓子虽然碎了,但总重量不会变,每个馓子的重量都差不多,用总重量除以单个馓子的重量,就得出了数量。
你是谁?尽可能多地说出你与周围人和事物的关系。