





还有一类需要研究的极限。我们已经研究了在接近一点 x = a 时的函数行为。然而在有些情况下,重要的是要理解当 x 变得非常大时,一个函数的行为如何。换句话说,我们感兴趣的是,研究当变量 x 趋于∞时函数的行为。我们想写出
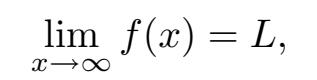
并以此表示,当
x
很大的时候,
f
(
x
)变得非常接近于值
L
,并保持这种接近的状态。(更多详情请参见附录A的A.3.3 节。)重要的是要意识到,写出
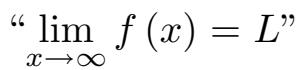 表示
f
的图像在
y
=
L
处有一条右侧水平渐近线。类似地,当
x
趋于−∞时,我们写出
表示
f
的图像在
y
=
L
处有一条右侧水平渐近线。类似地,当
x
趋于−∞时,我们写出
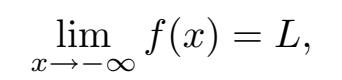
它表示当 x 变得越来越负(或者更确切地说,− x 变得越来越大)时, f ( x )会变得非常接近于值 L ,并保持接近的状态。当然,这对应于函数 y = f ( x )的图像有一条左侧水平渐近线。如果愿意,你也可以把这些转化为定义:
“
f
在
y
=
L
处有一条右侧水平渐近线”意味着
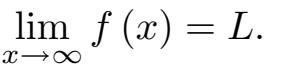
“
f
在
y
=
M
处有一条左侧水平渐近线”意味着
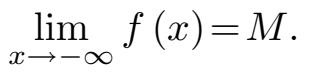
当然,像
y
=
x
2
这样的函数没有任何水平渐近线,因为当
x
变得越来越大时,
y
值只会无限上升。用符号表示,我们可以写作
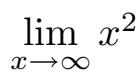 =∞。反过来,极限也有可能不存在。例如,
=∞。反过来,极限也有可能不存在。例如,
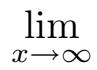 sin (
x
). sin (
x
)会变得越来越接近何值(并保持这种接近状态)呢?它只是在−1 和 1 之间来回振荡,因此绝不会真正地接近任何地方。此函数没有水平渐近线,也不会趋于∞或−∞;你所能作的最好回答是,
sin (
x
). sin (
x
)会变得越来越接近何值(并保持这种接近状态)呢?它只是在−1 和 1 之间来回振荡,因此绝不会真正地接近任何地方。此函数没有水平渐近线,也不会趋于∞或−∞;你所能作的最好回答是,
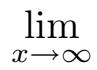 sin (
x
)不存在(DNE)。证明请参见附录A的A.3.4 节。
sin (
x
)不存在(DNE)。证明请参见附录A的A.3.4 节。
让我们回到上一节看到的函数
f
,其定义为
f
(
x
)=sin (1
/x
)。当
x
变得非常大时会怎么样呢?首先,当
x
很大时,1
/x
会非常接近于 0。由于sin (0)=0,那么sin (1
/x
)就会非常接近于 0.
x
越大,sin (1
/x
)就会越来越接近于 0。我的论证有点粗略,但希望能说服你相信

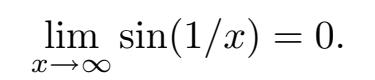
因此,sin (1 /x )在 y =0 处有一条水平渐近线。这就能够扩展我们之前画的 y =sin (1 /x )的图像,至少是向右边做扩展。我们仍旧担心当 x < 0 时会发生什么。事情不是太糟糕,因为 f 是一个奇函数。理由是
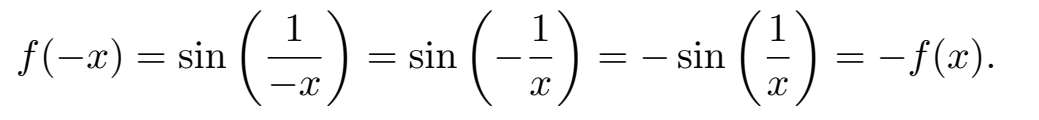
注意到我们使用了sin ( x )是 x 的奇函数的事实来由sin (−1 /x )得到−sin (1 /x )。这样一来,由于奇函数有一个很好的性质,就是其图像关于原点对称(参见 1.4 节),可以完整地画出 y =sin (1 /x )的图像,如图 3-8 所示。
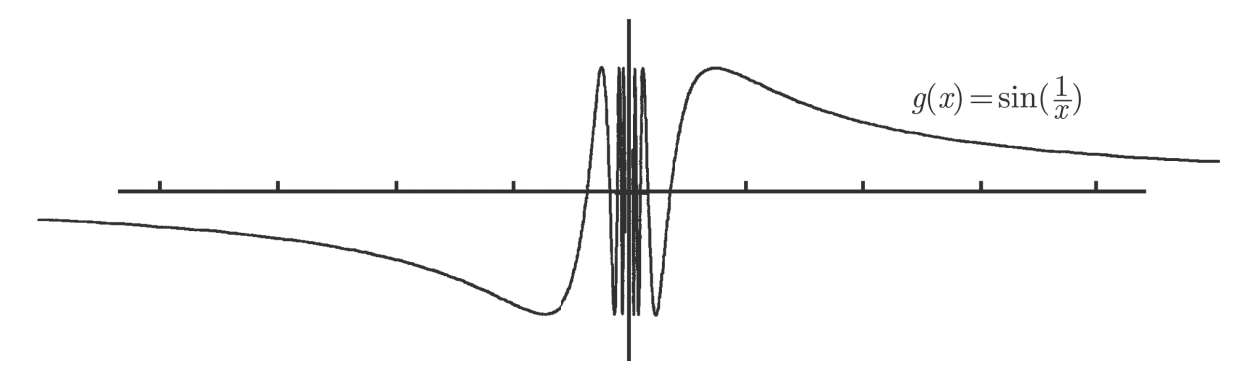
图3-8
同样,很难画出当 x 在 0 附近时的情况。 x 越接近 0,此函数就会振荡得越激烈。当然,该函数在 x =0 处无意义。在上图中,我选择避免在中间画得密密麻麻,而是把那里的激烈振荡留给你想象。
希望我们都认同 1 000 000 000 000 是一个大的数。那么−1 000 000 000 000呢?或许这会引起争议,但我要让你把它看作是一个大的负数,而不是一个小的数。举个小的数的例子,0.000 000 001,同时−0.000 000 001 也是一个小的数(更确切地说,是一个小的负数)。有趣的是,我们不打算把 0 看作是个小的数:它就是零。因此,下面就是我们对于大的数和小的数的非正式定义:
● 如果一个数的绝对值是非常大的数,则这个数是 大的 ;
● 如果一个数非常接近于 0(但不是真的等于 0),则这个数是 小的 。
尽管上述定义在我们的实际应用中很有帮助,但这实在是一个没有说服力的定义。“非常大”和“非常接近于 0”分别意味着什么?好吧,我们考虑极限
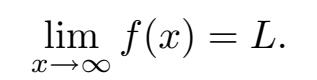
正如之前看到的,它表示当 x 是一个足够大的数时, f ( x )的值就会几乎等于 L 。可问题是,多大才是“足够大”呢?这取决于你想让 f ( x )距离 L 有多近!不过,从实际应用的角度出发,如果 y = f ( x )的图像看上去开始变得靠近在 y = L 的水平渐近线,那么这个数 x 足够大。当然,一切都依赖于函数 f 的定义,例如图 3-9 中的两种情况。
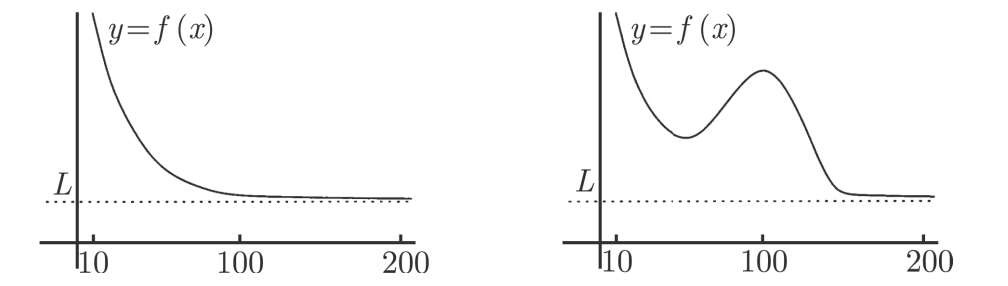
图3-9
在这两种情况下, f (10)都不在 L 的附近。在左图中,当 x 至少是 100 时, f ( x )看上去非常接近于 L ,因此,任何比 100 大的数都是大数。在右图中, f (100)远离 L ,因此,现在的 100 就不是足够大了。在这种情形下,你可能需要走到 200。那么你能够只选取一个像 1 000 000 000 000 这样的数,然后说它已经很大了吗?不可以,因为一个函数有可能一直起伏不定,直到比如 5 000 000 000 000 才变得趋于它的水平渐近线。这里的要点是,“大的”一词必须考虑到相关的某个函数或极限才有意义。幸好,没有最大,只有更大,往上还大有余地——甚至一个像 1 000 000 000 000这样的数,相对于 10 100 (古戈尔)来说还是相当小,而 10 100 与 10 1 000 000 比起来又是那么微不足道……顺便说一下,我们会经常使用术语“在∞附近”来代替“大的正的数”。(在字面意义上说,一个数不可能真的在∞附近,因为∞无穷远。不过在 x → ∞时的极限的语境中,“在∞附近”的说法还是说得通的。)
当然,所有这些也都适用于 x → −∞时的极限,你只需在上述所有大的正的数之前添加一个负号。在这种情况下,我们有时会说“在−∞附近”来强调我们所指的是大的负的数。
另一方面,我们会经常看到极限
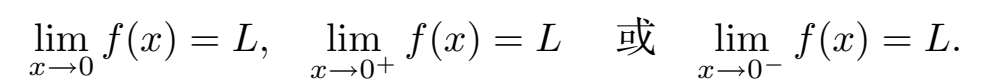
在上述三种情况下,我们知道,当 x 足够接近于 0 时, f ( x )的值几乎是 L 。 (对于右极限, x 还必须为正;而对于左极限, x 还必须为负。)那么 x 必须离 0 多近呢?这取决于函数 f 。因此,当说一个数是“小的”(或者“接近于 0”)时,必须结合某个函数或极限的语境来考虑,就像在“大的”情形中一样。
尽管这一番讨论让之前的非正式定义确实变得更严谨了一些,但它仍不算完美。如果你想了解更多,真的应该查看一下附录A的A.1 节和A.3.3 节。