




 一、时间是第四维
一、时间是第四维
第四维这个概念通常被神秘和怀疑所笼罩。我们这些只有长、宽、高的生物如何敢谈及四维空间呢?凭借我们全部的三维智力,有可能设想一个四维的超空间吗?一个四维的立方体或球体会是什么样子呢?我们说“想象”一条尾巴披鳞、鼻孔喷火的巨龙,或者一架带有游泳池、机翼上有两个网球场的超级客机时,实际上是在心灵中描绘这些东西真的突然出现在我们面前时的样子。我们是以那个所有普通物体(包括我们自己在内)都位于其中的大家所熟悉的三维空间为背景来描绘这幅图像的。如果这就是“想象”一词的含义,我们就无法以普通三维空间为背景来想象一个四维的物体,一如我们无法将三维物体压入平面。不过且慢,在某种意义上我们的确可以将一个三维物体压入平面,那就是在平面上画出这个三维物体。不过,在所有这些情况下,我们当然不是用一台水压机或任何其他物理的力量来实现的,而是用所谓的几何“投影”法进行的。由图24立即可以看出将物体(例如马)压入平面的这两种方法的区别。
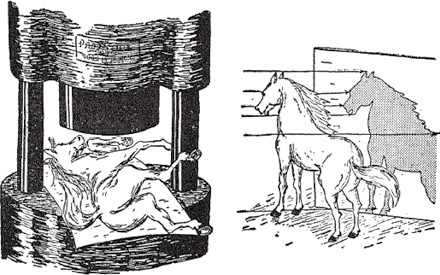
图24 将一个三维物体“压”入二维表面的错误方法和正确方法
通过类比,我们现在可以说,虽然不可能把一个四维物体完全“压”入三维空间,但可以讨论各种四维物体在我们这个三维空间中的“投影”。不过要记住,正如三维物体的平面投影是二维图形或平面图形,四维超物体在我们这个普通三维空间中的投影是立体图形。
为了把问题说得更清楚一些,我们先来考虑生活在面上的二维影子生物会如何构想一个三维立方体。不难想象,作为优越的三维生物,我们可以从上面即从第三个方向来打量二维世界。将立方体“压”入平面的唯一途径就是以图25所示的方法将它“投影”到那个平面上。旋转这个立方体,可以得到各种其他投影。通过观察这些投影,我们的二维朋友们至少能对这个被称为“三维立方体”的神秘形体的性质形成某种认识。他们无法“跳出”自己的面,像我们一样来看这个立方体。不过仅仅通过观察投影,他们也能说(比如)这个立方体有八个顶点和十二条边。现在看图26,你会发现自己的处境和那些只能看到普通立方体在面上投影的可怜的二维影子生物完全相同。事实上,图中那家人正在惊愕万分地研究的那个复杂的古怪结构,正是一个四维的超正方体在我们这个普通三维空间中的投影。

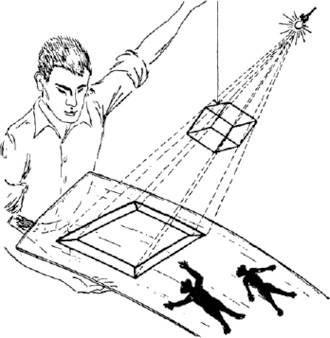
图25 二维生物们正在惊奇地打量一个三维立方体在其表面上的投影
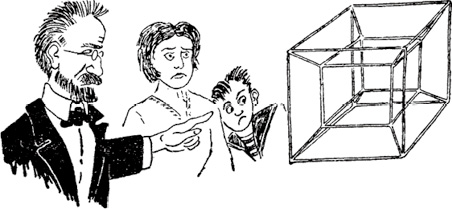
图26 四维空间的来客!一个四维超正方体的正投影
认真考察这个形体,你很容易看到让图25中的影子生物困惑不已的那些特征:普通立方体在平面上的投影是两个正方形,一个套在另一个里面,且顶点与顶点相连;而超正方体在普通空间中的投影则是两个立方体,一个套在另一个里面,顶点也以类似的方式相连。数一数就会看到,一个超正方体共有16个顶点、32条边和24个面。好一个正方体,不是吗?
现在我们来看看四维球体是什么样子。为此,我们最好先看一个较为熟悉的例子,即一个普通球体在平面上的投影。例如设想将一个标记有大陆和海洋的透明球体投射到一面白墙之上(图27)。在这一投影中,两个半球当然会彼此重叠,而且从投影上看,我们也许会以为美国纽约和中国北京距离很近。但这只是一种表面的印象。事实上,投影上的每一点都代表实际球体上两个相对的点,一架从纽约飞往中国的飞机,它在球体上的投影将先移到平面投影的边缘,然后再返回来。虽然两架不同飞机在图上的投影可能会重叠,但如果它们“实际”在地球的两侧飞行,那是不会相撞的。
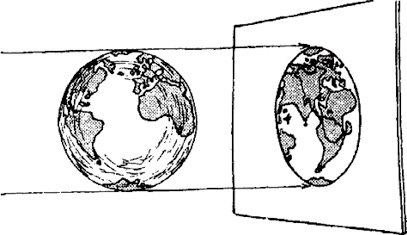
图27 地球的平面投影
这些便是普通球体的平面投影的性质。只要对想象力稍作发挥,我们便不难看出四维超球体的空间投影是什么样子。正如普通球体的平面投影是两个(点对点)叠在一起、只沿外圆周相连的圆盘,超球体的空间投影也一定是两个彼此交叠且沿外表面相连的球体。关于这种特异的结构,我们已经在上一章作为类似于封闭球面的三维封闭空间的例子作了讨论。这里只需补充一句:四维球体的三维投影不过就是我们在那里讨论的由两个沿整个外皮长在一起的普通苹果所形成的双苹果罢了。
同样,使用这种类比法,我们也能回答关于四维形体性质的其他许多问题,尽管我们无论如何也没法在我们的物理空间中“想象”出第四个独立的方向。
不过,只要再稍作思考,你就会发现,根本没有必要把第四个方向看得很神秘。事实上,有一个我们几乎每天都在用的词可以表示物理世界中这第四个独立的方向,那就是“时间”。我们常常用时间和空间来描述周围发生的事件。谈到宇宙中发生的任何事情时,无论是在街上邂逅了一个朋友,还是遥远星体的爆发,我们通常不仅会说它在哪里发生,还会说它是何时发生的。于是,除了表示空间位置的三个方向要素之外,我们又增加了一个要素——时间。
如果作进一步思考,你还可能意识到,任何实际物体都有四个维度:三个空间维度,一个时间维度。比如你所住的房屋就是沿长、宽、高和时间延展的。时间的延展从盖房时算起,一直到它最后被烧毁、被某个拆迁公司拆掉或因年久失修而倒塌为止。
的确,时间方向与空间的三维很不相同。时间间隔是由钟表度量的:嘀嗒声表示秒,叮咚声表示小时,而空间间隔则是由尺子度量的。你能用同一把尺子来度量长、宽、高,却不能把尺子变成钟表来度量时间。此外,你在空间中可以前移、后移或上移,然后再回来,而在时间中你却退不回来,只能从过去到将来。不过,尽管时间方向与空间的三个方向之间存在着所有这些区别,我们仍然可以把时间作为物理世界的第四个方向,不过别忘了它与空间不大相同。
在选择时间作为第四维时,想象本章开头讨论的四维形体要简单得多。例如,你还记得四维正方体的投影所切出的那个奇特形体吗?它竟然有16个顶点、32条边和24个面!难怪图26中的那些人盯着这个几何怪物会瞠目结舌。
不过从我们的新观点来看,四维正方体只是个存在了一段时间的普通立方体罢了。假定你在5月7日用12根铁丝制成了一个立方体,一个月后又把它拆掉。那么,这样一个立方体的每一个顶点都应被看成沿时间方向有长为一个月的一条线。你可以给每个顶点挂一本小日历,每天翻一页以显示时间的前进。
现在很容易数出这个四维形体的边数。它刚开始存在时有12条空间边,以及描述各个顶点延续时间的8条“时间边”,结束存在时又有12条空间边,
 因此总共有32条边。用类似的方法可以数出它有16个顶点:5月7日有8个空间顶点,6月7日又有8个空间顶点。作为练习,请读者以同样的方式数一数我们四维形体的面数。在此过程中要记住,其中一些面是原立方体的普通正方形面,其他面则是立方体原来的边从5月7日延伸到6月7日所形成的“半空间半时间”面。
因此总共有32条边。用类似的方法可以数出它有16个顶点:5月7日有8个空间顶点,6月7日又有8个空间顶点。作为练习,请读者以同样的方式数一数我们四维形体的面数。在此过程中要记住,其中一些面是原立方体的普通正方形面,其他面则是立方体原来的边从5月7日延伸到6月7日所形成的“半空间半时间”面。
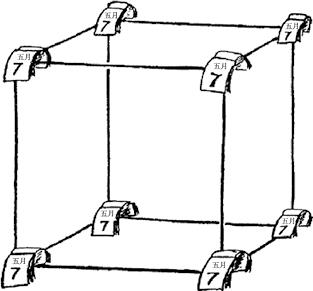
图28
我们这里针对四维立方体所讲的内容当然也适用于任何其他几何体或物体,无论是死的还是活的。
特别是,你可以设想自己是一个四维形体,类似于一根长长的橡胶棒从你出生之时延伸到你生命结束。不幸的是,我们在纸上画不出四维物体,因此在图29中,我们尝试以二维影子人为例来说明这种想法,他把与他所生活的二维平面垂直的空间方向认作时间方向。这幅图只描绘了这个影子人整个生命的很小一部分,整个生命过程需要用一根长得多的橡胶棒来表示:开端很细,此时他是婴儿,在很多年里一直变动不定,直到死时才获得恒定的形状(因为死人不会动),然后开始解体。
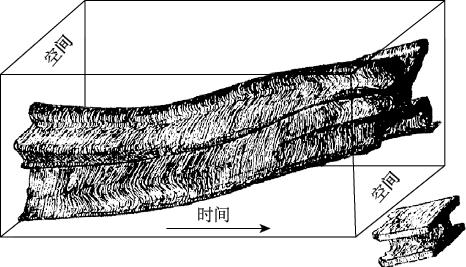
图29
说得更确切一些,这根四维棒是由无数分离的纤维组成的,每根纤维都由分离的原子所组成。在整个生命过程中,大多数纤维保持成一束,只有少量纤维在理发或剪指甲时离去。由于原子是不灭的,所以人死后的身体分解实际上应被视为各个纤维朝四面八方分散开来(也许除了形成骨骼的那些纤维)。
用四维时空几何的语言来说,这样一条代表每一个物质微粒历史的线被称为它的“世界线”。同样,我们把形成一个复合体的一束世界线称为“世界束”。
图30给出了一个天文学的例子,显示了太阳、地球和彗星的世界线。
 和前面那个例子一样,我们让时间轴与二维空间(地球轨道平面)垂直。在这幅图中,太阳的世界线由一条与时间轴平行的直线来表示,因为我们认为太阳是不动的。
和前面那个例子一样,我们让时间轴与二维空间(地球轨道平面)垂直。在这幅图中,太阳的世界线由一条与时间轴平行的直线来表示,因为我们认为太阳是不动的。
 地球的轨道非常接似于圆,地球的世界线是一条围绕太阳世界线盘旋的螺旋线,而彗星的世界线则先靠近、后远离太阳的世界线。
地球的轨道非常接似于圆,地球的世界线是一条围绕太阳世界线盘旋的螺旋线,而彗星的世界线则先靠近、后远离太阳的世界线。
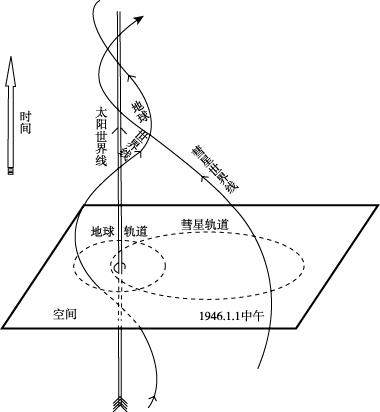
图30
我们看到,从四维时空几何的角度来看,宇宙的地形学和历史融合成了一幅和谐画面。我们只需考虑一束代表个体原子、动物或星辰运动的缠结在一起的世界线就可以了。