




 2.2 曲线运动
2.2 曲线运动
抛体运动——物体在地面附近不大的范围内仅在重力作用下的运动。被抛物体只受恒定的重力作用,故做匀变速曲线运动,其加速度为重力加速度g,其速度变化的方向总是竖直向下的。
(1)平抛运动
物体水平抛出后的运动,可看成是水平方向的匀速直线运动和竖直方向的自由落体运动这两个分运动的合成。
(2)斜抛运动
物体斜向上或斜向下抛出后的运动。下面以斜上抛运动为例讨论:
1)特点
加速度a=g,方向竖直向下。初速度方向与水平方向成一夹角θ斜向上,θ=90°为竖直上抛运动;θ=0为平抛运动。
2)常见的处理方法
①将斜上抛运动分解为水平方向的匀速直线运动和竖直方向的竖直上抛运动,这样有:
在水平方向
v x =v 0 cosθ,x=v 0 cosθ·t
在竖直方向
v
y
=v
0
sinθ-gt,y=v
0
sinθ·t
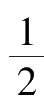 gt
2
gt
2
由此可得如下特点:a.斜向上运动的时间与斜向下运动的时间相等;b.从轨道最高点将斜抛运动分为前后两部分,这两部分具有对称性,如同一高度上的两点,速度大小相等,速度方向与水平力线的夹角大小相等。
②将斜抛运动分解为沿初速度方向的斜向上的匀速直线运动和自由落体运动两个分运动,用矢量合成法则求解。
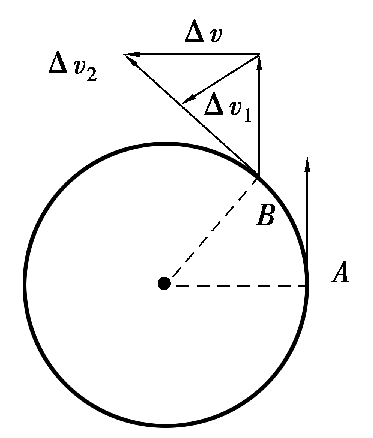
图 2.15
③处理在斜面上的斜抛运动问题时,一般将沿斜面和垂直斜面方向分别作为x、y轴,再分别分解初速度和加速度后用运动学公式解题。
做圆周运动的质点,速度不仅大小可以变化,方向也在不断变化。如图2.15所示,质点在沿圆周由A到B的过程中,其速度的增量Δv=Δv 1 +Δv 2 。其瞬时加速度
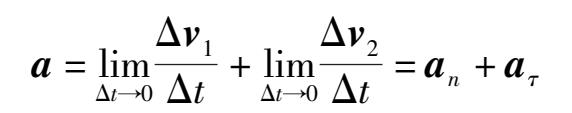
上式中,a
n
为向心加速度,它描述速度方向的变化快慢,大小为
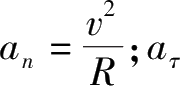 为切向加速度,它描述速度大小的变化快慢。对匀速圆周运动而言,a
τ
= 0,而对一般曲线运动,
为切向加速度,它描述速度大小的变化快慢。对匀速圆周运动而言,a
τ
= 0,而对一般曲线运动,
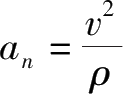 ρ式中ρ为质点所在位置的曲线的曲率半径。
ρ式中ρ为质点所在位置的曲线的曲率半径。
刚体定轴转动时,其上各点都绕转轴做圆周运动,且各点的角位移θ、角速度ω、角加速度β都相同。
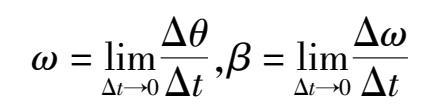
当β为常量时,刚体做匀变速转动,其运动规律可类比于匀变速直线运动,因而有
ω=ω
0
+βt,θ=θ
0
+ω
0
t+
 βt
2
,ω
2
=
βt
2
,ω
2
=
 +2β(θ-θ
0
)
+2β(θ-θ
0
)
做定轴转动的刚体,其上一点(到转轴的距离为R)的线速度v、切向加速度a τ 、向心加速度a n 与刚体的角速度ω和角加速度β的关系是
v=ωR,a
T
=βR,a
n
=
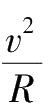 =ω
2
R
=ω
2
R
匀速圆周运动是一种周期性运动,其规律的描述不同于匀变速运动。在圆周运动中,位移、速度与时间的关系不再是研究的重点,其重点是研究周期、角速度、速率、半径等物理量与加速度的联系,从而进一步研究运动和力的关系。在一般圆周运动中,要注意加速度一方面描述了速度大小的变化快慢,另一方面又描述了速度方向的变化快慢。
例1 一圆盘沿顺时针方向绕过圆盘中心O并与盘面垂直的固定水平转轴以匀角速度ω=4.43rad/s转动,圆盘半径r=1.00m,圆盘正上方有一水平天花板,如图2.16(a)所示。设圆盘边缘各处始终有水滴被甩出。现发现天花板上只有一点处有水。取重力加速度大小g=9.80m/s 2 。求:
(1)天花板相对于圆盘中心轴O点的高度;
(2)天花板上有水的那一点的位置坐标。
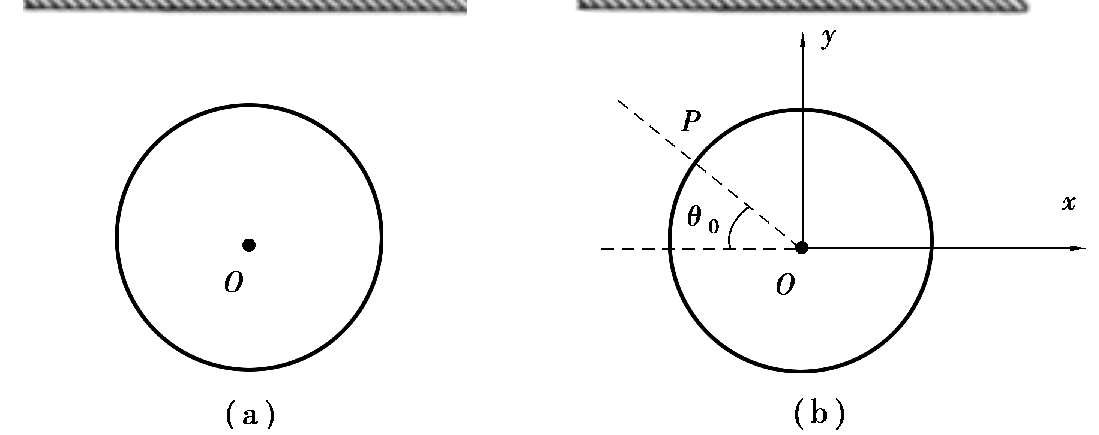
图 2.16
解 (1)在圆盘所在平面内建立平面直角坐标系,使盘心O为原点,x轴水平向右,y轴竖直向上。只有第二象限的圆盘边缘甩出的水滴才可能到达天花板上某固定点;而不是打到天花板上某一区域(不止一个点),或者打不到天花板上。
水滴甩出时的初速度大小是恒定的
v 0 =ωr
水滴从P点甩出时,设OP与x轴负向成θ 0 ,如图2.16(b)所示,其x和y分量分别为
v ox =v 0 cosθ 0 ,x 0 =rcosθ 0
v oy =v 0 sinθ 0 ,y 0 =rsinθ 0
取水滴从P点甩出时为计时零点,水滴的x、y坐标与t的关系式为
x=x
0
+v
0x
t,y=y
0
+v
0y
t-
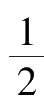 gt
2
gt
2
现对某一特定的θ值,求y的最大值
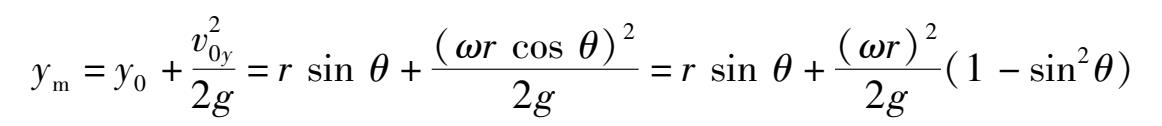
对变元sinθ配方后,得
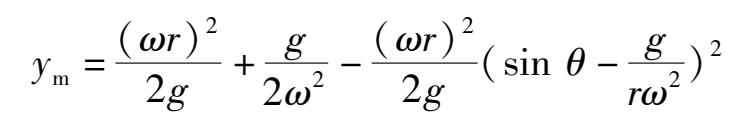
当
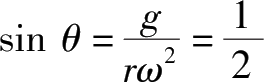 ,即θ=30°时,y
m
=1.25m。
,即θ=30°时,y
m
=1.25m。
依题意,上式即为天花板相对圆盘中心轴O点的高度。
(2)代入θ=30°,有
x= -r cos 30°+
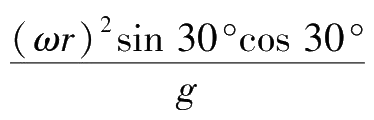 =0
=0
所以天花板上有水的那一点的位置坐标为(0,1.25 m)。
例2
如图2.17(a)所示,一光滑斜面与水平面夹角为α,由斜面下端O向上斜抛一个小球,小球的初速度为v,抛射方向与斜面夹角为
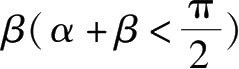 。小球的轨迹在如图2.17(a)所示的竖直平面内。已知小球与斜面在每次碰撞时,速度垂直于斜面方向的分量在碰撞后是碰撞前的e倍,e<1;小球在第n次碰撞时恰好回到O点。求:α、β与e、n之间所满足的关系式。
。小球的轨迹在如图2.17(a)所示的竖直平面内。已知小球与斜面在每次碰撞时,速度垂直于斜面方向的分量在碰撞后是碰撞前的e倍,e<1;小球在第n次碰撞时恰好回到O点。求:α、β与e、n之间所满足的关系式。
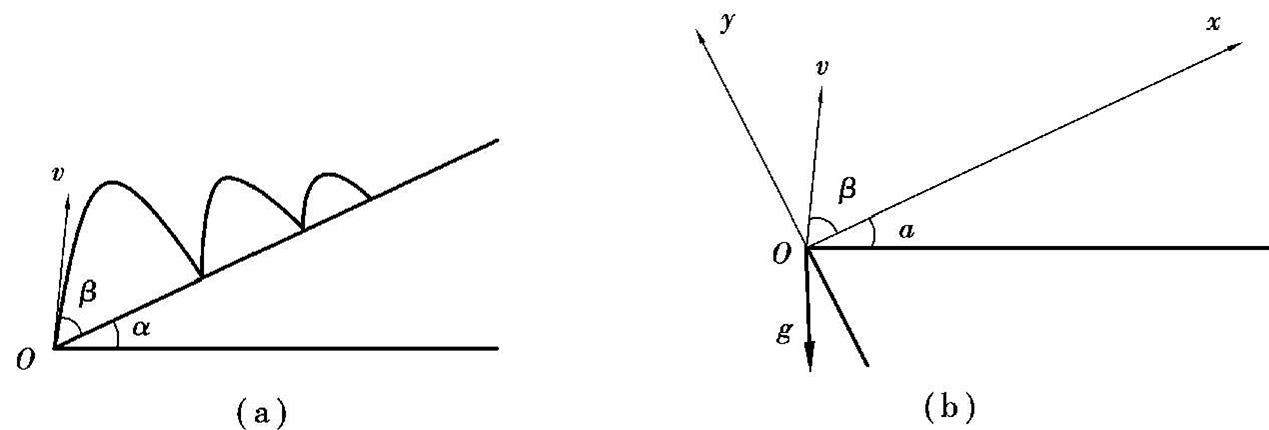
图2.17
解 以斜面方向为x轴,垂直于斜面方向为y轴建立坐标系,原点为O,如图2.17(b)所示,则有
v x =vcosβ,v y =vsinβ
a x =gsinα,a y =gcosα
设从抛出小球到小球落回O点的时间为t,则在x方向有
0=v
x
t-
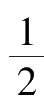 a
x
t
2
a
x
t
2
小球第一次掉到斜面的时间t 1 满足
v
y
t
1
-
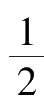 a
y
t
a
y
t
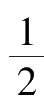 =0
=0
即
t
1
=
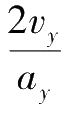
同时,小球第一次掉到斜面上时的速度
v' y =v y -a y t 1 =-v y
依题意,小球第一次反弹的速度为ev y ,所以在y轴方向可得
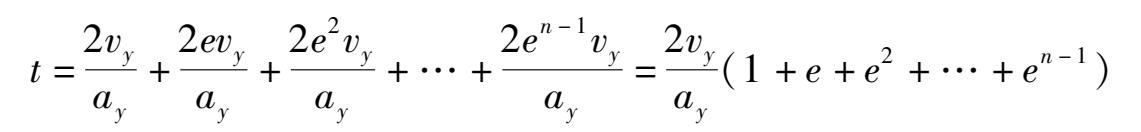
由以上各式可得α、β与e、n之间所满足的关系式
1+e+e 2 +…+e n- 1 =cotαcotβ
即
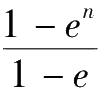 =cotαcotβ
=cotαcotβ
例3 图2.18(a)所示为用三角形刚性细杆AB、BC、CD连成的平面连杆结构图。AB和CD杆可分别绕过A、D的垂直于纸面的固定轴转动,A、D两点位于同一水平线上。BC杆的两端分别与AB杆和CD杆相连,可绕连接处转动(类似铰链)。当AB杆绕A轴以恒定的角速度ω转到图2.18(a)所示的位置时,AB杆处于竖直位置。BC杆与CD杆都与水平方向成45°,已知AB杆的长度为l,BC杆和CD杆的长度由图给定。求此时C点加速度a C 的大小和方向(用与CD杆之间的夹角表示)。
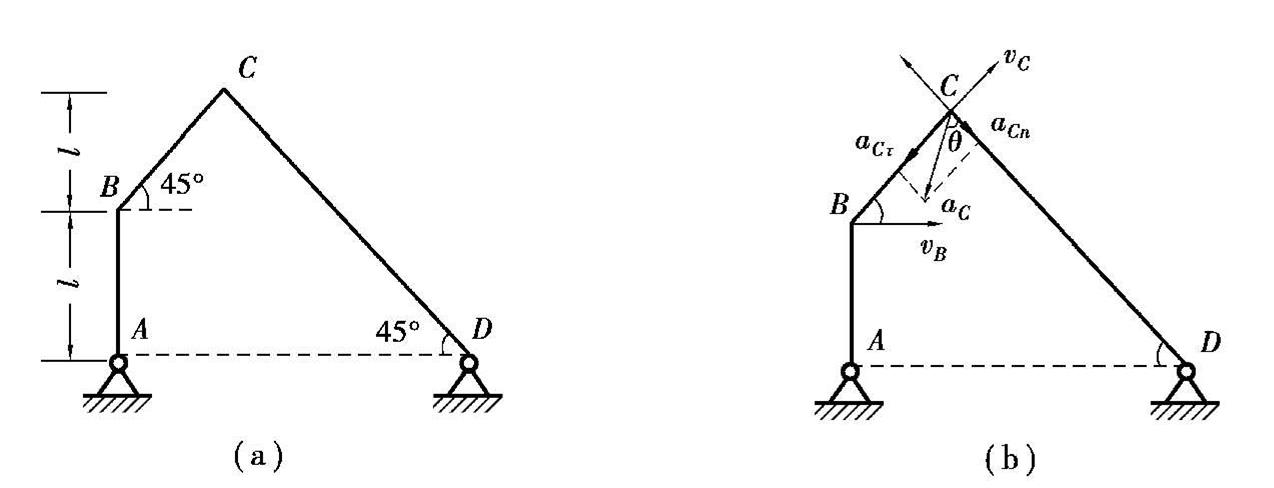
图 2.18
解 因B点绕A轴做圆周运动,其速度的大小为

B点的向心加速度大小为

由于是匀速转动,B点的切向加速度为0,故a B 也是B点的加速度,其方向沿BA方向。因C点绕D轴做圆周运动,其速度的大小用v C 表示,方向垂直于杆CD,由图2.18(b)可知,其方向沿杆BC方向,因BC是刚性杆,所以B点和C点沿BC方向的速度必相等,故有

此时杆CD绕D轴按顺时针方向转动,C点的法向加速度

由图2.18(b)可知
CD=22l
由③④式可得

其方向沿CD方向。
而C点沿垂直杆CD方向的加速度,即切向加速度为a Cτ 。因BC是刚性杆,所以C点相对B点的运动只能是绕B的转动,C点相对B点速度方向必垂直于杆BC。
设v CB 表示其速度的大小,根据速度的合成公式,有
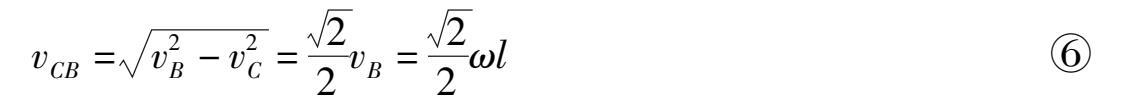
因为C点绕B做圆周运动,相对B点的向心加速度
a
cB
=
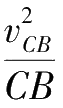
因为
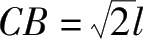 ,故有
,故有

其方向垂直于杆CD。
由②式及图2.18(b)可知,B点的加速度沿BC杆的分量为
(a
B
)
cB
=a
B
cos
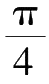
所以,C点相对于A点的加速度沿垂直杆CD方向的分量
a
CT
=a
CB
+(a
B
)
BC
=
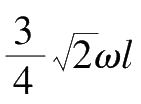
C点的总加速度为C点绕D点做圆周运动的法向加速度a Cn 与切向加速度a Cτ 的合加速度,即

a C 的方向与杆的CD间夹角为
θ=arctan
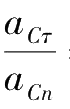 = arctan 6=80.54°
= arctan 6=80.54°
1.如图2.19所示,沿水平方向向一面竖直光滑的墙壁抛出一个弹性小球A,抛出点离水平地面的高度为h,距离墙壁的水平距离为s,小球与墙壁发生弹性碰撞(碰撞后速度大小保持不变)后,落在水平地面上,落地点距墙壁的水平距离为2s。求小球抛出时的初速度。
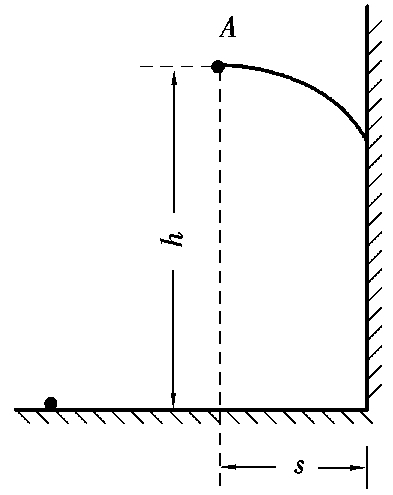
图 2.19
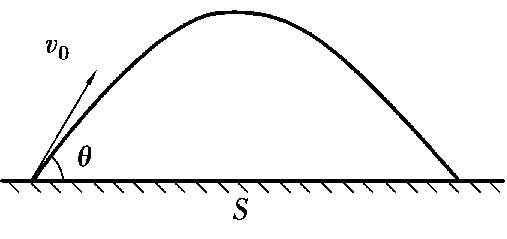
图 2.20
2.物体做如图2.20所示的斜抛运动。(1)已知抛出速度为v 0 与抛射角θ,求物体在水平面的落点与抛出点的距离s;(2)(该问用到了动量守恒)若一个人站在光滑冰面上,以相对自己的速度v 0 斜向上抛出一个球,当小球下落至抛出点高度时,水平位移为L。设人与球的质量分别为M和m,求抛出速度v 0 的最小值,以及小球抛出时速度与水平方向的夹角θ。
3.一只苍蝇在高H处,以速度v平行桌面飞行,在某一时刻发觉就在它的正下方有一滴蜂蜜,苍蝇借助于翅膀可以向任何方向加速,但加速度大小不超过a。试求苍蝇能够飞到蜂蜜所在处的最短时间(设想问题发生在宇宙空间,重力不存在)。
4.公园的转椅以恒定的角速度ω绕其竖直对称轴在水平面内匀速转动,转椅上的人以相对转椅v的速度平抛一小球。如图2.21所示,为使小球能击中转椅架底部中心点O,试求v的大小和方向(已知小球抛出点比O点高h,与竖直转轴的距离为R)。
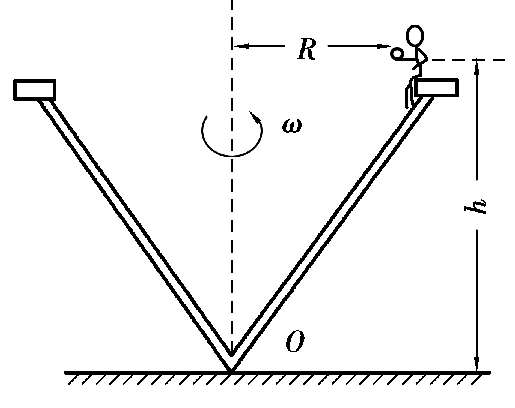
图 2.21
5.如图2.22所示,有一半径为R的刚性圆环竖直地在刚性水平地面上做纯滚动,圆环中心以不变速度v 0 在圆环平面内水平向前运动,求圆环上与圆心等高的P点的瞬时速度、切向加速度和法向加速度。
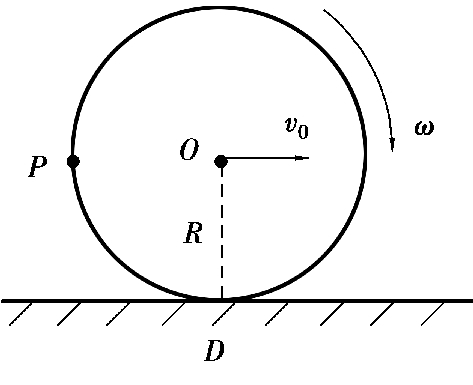
图 2.22
6.如图2.23所示,AC杆的A端以匀速v沿水平地面向右运动,在运动时杆恒与一半圆周相切,半圆周的半径为R,当杆与水平线的交角为θ时,求此时:
(1)杆上与半圆相切点B的速度大小v B ;
(2)杆的角速度ω;
(3)杆上AB间中点的速度大小v 中 ;
(4)杆与圆柱接触点B′的速度大小v B′ 。
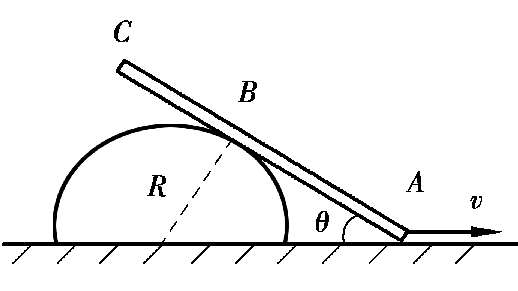
图 2.23

参考答案与解析