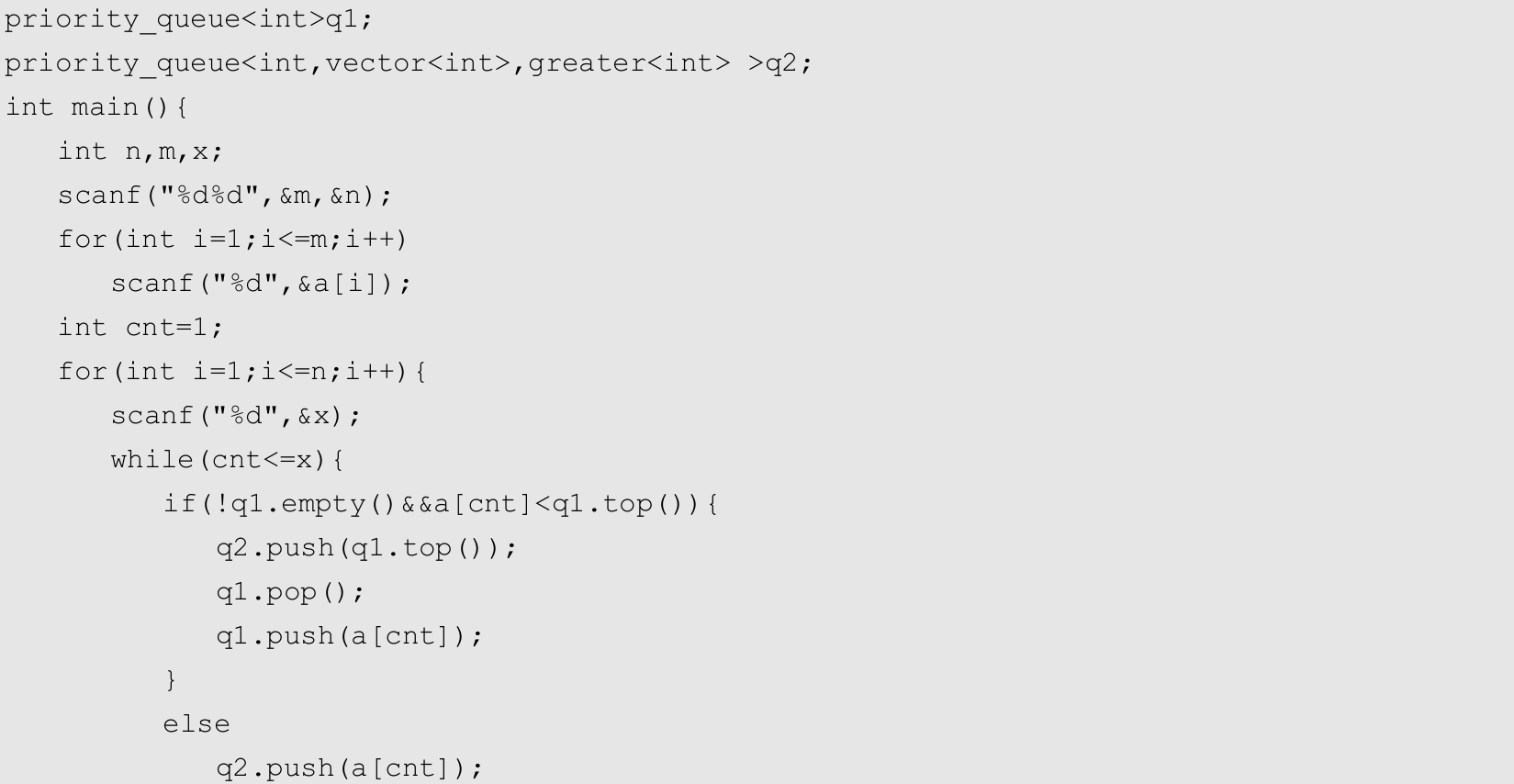
priority_queue是一个优先队列,优先级高的最先出队,默认最大值优先。内部实现为堆,因此出队和入队的时间复杂度均为 O (log n )。可以自定义优先级控制出队顺序,如果是数值,则也可以采用加负号的方式实现最小值优先,优先队列不支持删除堆中的指定元素,只可以删除堆顶元素,如果需要删除指定元素,则可以采用懒操作。使用priority_queue时,需要引入头文件#include <queue>。
优先队列的成员函数如下。
● push( x ): x 入队。
● pop():出队。
● top():取队头。
● size():返回队中的元素个数。
● empty():判断队空,若为空则返回true。
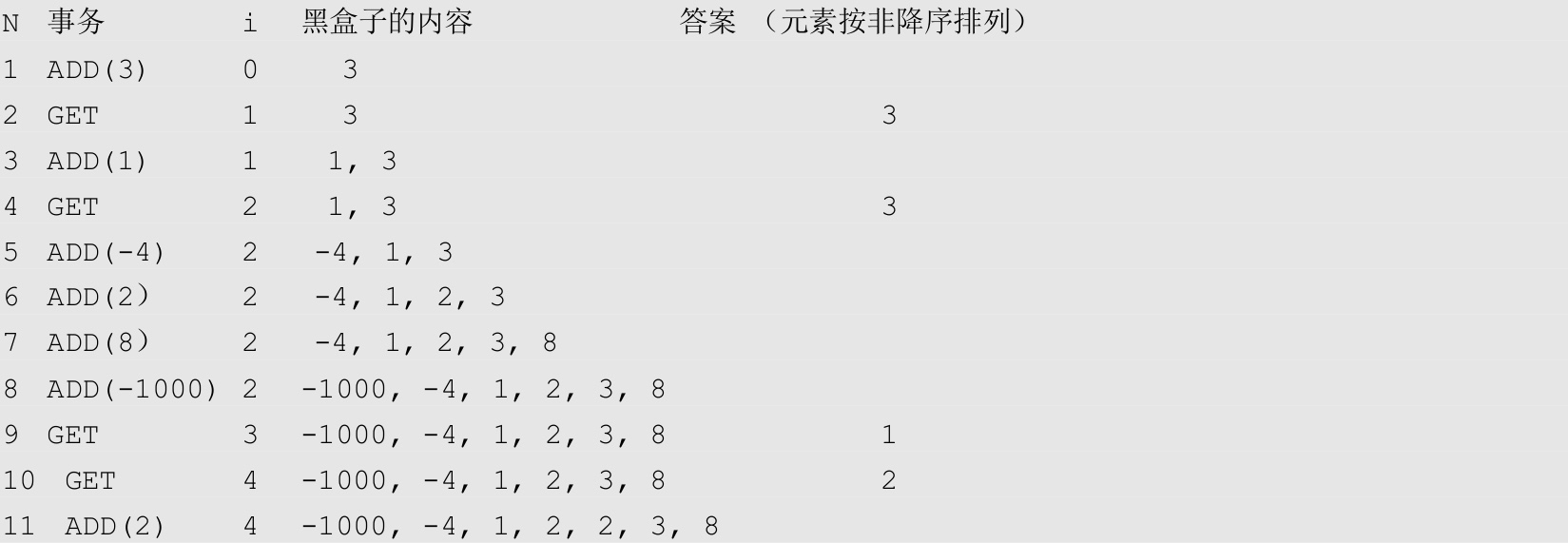
题目描述(POJ1442): 黑盒子代表一个原始数据库,保存一个整数数组和一个特殊的 i 变量。在最初的时刻,黑盒子是空的, i =0。黑盒子处理一系列命令(事务),有以下两种类型的事务。
● ADD( x ):将元素 x 放入黑盒子。
● GET:将 i 增加1,并给出包含在黑盒子中的所有整数中第 i 小的值。第 i 小的值是黑盒子中按非降序排序后的第 i 个位置的数字。
示例如下。
写一个有效的算法来处理给定的事务序列。ADD和GET事务的最大数量均为30 000。用两个整数数组来描述事务的顺序。
(1)A(1),A(2),…,A( M ):包含在黑盒子中的一系列元素。A值是绝对值不超过2 000 000 000的整数, M ≤30 000。对于示例,序列A =(3, 1, -4, 2, 8, -1000, 2)。
(2) u (1), u (2),…, u ( N ):表示在第1个,第2个,…,第 N 个GET事务时包含在黑盒子中的元素个数。对于示例, u =(1, 2, 6, 6)。
假设自然数序列 u (1), u (2),…, u ( N )按非降序排序, N ≤ M 且每个 p (1≤ p ≤ N )对不等式 p ≤ u ( p )≤ M 都有效。由此得出这样的事实:对于 u 序列的第 p 个元素,执行GET事务,给出A(1),A(2),…,A( u ( p ))序列第 p 小的数。
输入: 输入包含 M , N ,A(1) ,A(2) ,…,A( M ) , u (1) , u (2) ,…, u ( N )。
输出: 根据给定的事务顺序输出答案序列,每行一个数字。

可以采用两个优先队列:一个是最大值优先队列 q 1 ,保存前 i -1大的数;另一个是最小值优先队列 q 2 ,保存从 i 到序列末尾的数。 q 2 的堆顶就是要查询的第 i 小的数。
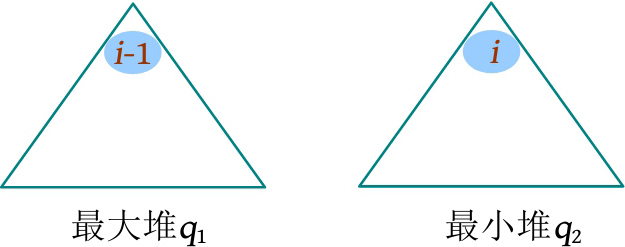
(1)用cnt计数,控制放入黑盒子的元素个数。
(2)读入 u ( i ),如果cnt≤ u ( i ),则重复以下操作:如果 q 1 不空且 a [cnt]< q 1 .top(),则说明 a [cnt]属于前 i -1大的数,因此将 q 1 堆顶放入 q 2 , q 1 堆顶出队,将 a [cnt]放入 q 1 ;否则,直接将 a [cnt]放入 q 2 。cnt++。
(3)输出 q 2 的堆顶(第 i 小的数)。
(4)因为查询第 i 小时, i 每次都增1,因此每次处理完毕后,都需要将 q 2 中的堆顶放入 q 1 , q 2 堆顶出队。