




计算思维左右离不开一个概念,就是 算法 。
目前业界公认,术语“算法”源自公元9世纪的数学家、天文学家花剌子米(al-Khawārizmi)。花剌子米写了不少数学书,“算法”这个词就来自他名字的拉丁文音译。
但是,不看这个词的话,大多数历史学家认为,巴比伦的泥板是世界上第一个已知的算法。在这种泥土烧成的平板上,巴比伦人开发和保存了一种使用楔形数字进行计数的数字系统。
图2-1
还有些算法被记录在古希腊的纸上,诸如杰拉萨的尼科马修斯(Nicomachus)、欧几里得(Euclid)等学者奠定了现代数学的基础。为了简化其想法,使之具备可理解性和适用性,他们将其中许多想法表示为分步操作,和我们的计算机算法很相似。
算法在拉丁语中叫“Algoritmi”,意思是“十进制数系统”,算法在这样一个含义下使用了几个世纪。后来,算法的非正式定义演变成“一系列精确定义的操作规则”,所以菜谱、法律流程也都可以算作算法。
现代算法的概念在19世纪以英语出现,并在20世纪50年代开始流行,这是由第一台商用计算机的出现而引起的。计算机大师图灵严格定义了“计算”这个概念,证明了图灵机可以模拟任何一个算法,引起了业界的广泛兴趣。
从此以后,人们普遍认为,“算法是计算机的过程和公式,它们将您的问题转化为答案”。
算法本身可以有多种表现形式,可以是自然语言、流程图、伪代码、编程语言等。好的算法需要被精心设计,可以适用于多种场景。我在斯坦福计算机系读博士期间,经常会在系里碰见戴着自行车头盔的当代算法大师唐纳德·克努特,他自取的中文名叫高德纳。他是1974年图灵奖的获得者,TeX(文本排版系统)的发明者,被称为“算法分析之父”。高德纳有一段关于算法的著名引言:
我们希望在某种松散的美学意义上寻求好的算法。一个标准是执行该算法所需的时间;另一个标准是该算法对计算机的适应性,也就是简单和优雅。
“简单”代表“快”,“优雅”代表“小”。快而小,是算法的终极目标。
说起当代算法大师高德纳,他与算法的结缘来自他13岁时一场关于糖果名称的组词比赛。
在20世纪中叶,计算机编程刚刚诞生的那些年,有一家叫Ziegler(齐格勒)的糖果公司为了促销一种叫Giant Bar(巨人吧)的棒棒糖,在学校中办了一个比赛,看谁能用Ziegler’s Giant Bar中的字母排列组合出最多的单词,这是一个界定清晰明确的问题,也正是高德纳喜欢的那类问题。
“我有一种强迫症,而这个小比赛让我产生了对数字离散问题的兴趣。并且,我也很热爱钻研大量信息。”高德纳说。
在他家的地下室中,高德纳系统性地翻阅了他家那本2 000页厚的Funk & Wagnalls(美国出版商)无删节版词典。他甚至说服父母相信自己生病了,这样两周时间都没去上学,而是把时间投入这个问题。基于这些可能组成糖果名称的字母,他标注了以Aa、Ab和Ba等可能在单词前面的字母串,并将它们做成了索引卡片。之后,他开始检索词典中满足条件的条目。他发现词典中有些部分可以完全跳过,比如以字母C或BU开头的单词所在的部分。
赛事举办方预计最后的胜者能找到大约2 000个单词,而高德纳找到了4 700多个。他为他的班级赢得了在电视上露脸以及获得巧克力的奖励。
在那以后,他还将继续为自己赢得更多“巧克力”,包括第一届格蕾丝·穆雷·赫柏(Grace Murray Hopper)奖、美国国家科学奖章和1974年图灵奖。
高德纳将自己对离散数字问题和大量信息的热爱融入了他的巨著《计算机程序设计艺术》,这套书从1962年他还是一个研究生时就已经开始写了,但到现在还未完成。
1968年,他出版了该书的第一卷,目前该卷已经印了27版。第二卷和第三卷分别出版于1969年和1973年。1968年他已经是斯坦福大学的一位计算机科学教授了,但他一直担心教职工作会妨碍自己写完这套书。因此他在1990年告假,接着在1993年退休,打算余生都用来完成这套七卷巨著。现在,他已经83岁了,仍在努力撰写第四卷的B部分,他预计这一卷至少有A到F共6部分。
在这本书里,我不仅仅希望把算法这个概念教给大家,还希望让大家真正看到计算机的算法是怎样一步步工作的。这一章,我将介绍所有计算机应用都离不开的 排序算法 。
图2-2
世上一切皆有次序,从播种到花开,春夏秋冬,四季更迭。排序在生活中的一个典型例子就是按一定的规则排队。排序有非常多的应用场景,比如孩子在体育课上按高矮排队,书店的图书按字母排序,字典里的字按笔画排序,考试成绩按分数排序。前面我们提到过抖音的短视频排序,淘宝的商品排序,游戏榜单的比分排序,这些都是排序。你在一个电商网站,比如在京东、淘宝买东西,它们的商品可以按销售量排,按评论数排,也可以按价格排。在手机App,比如美团、点评里,商家可以按距离远近排或按均价排。这些也都是排序。排序是其他算法发挥作用的基础,比如搜索算法往往基于已经排好的物品,才能快速找到目标。
你也许会觉得排序是一件简单的事。从概念上看,排序是比较容易理解的,所以这章我们用排序来引入,看看计算机算法是怎么回事儿。我们也会看到,给少量物品排序并不难,但是如何有效地给成千上万个物品排序,还是很有讲究的。
图2-3
逻辑清晰的计算机如何给一些东西排序?让我们先来看一个简单的例子——抓牌。打牌的时候,如果你决定把所有抓到的牌从小到大排在手里,你会怎么做?
你也许会先抓第一张拿在手里。从第二张牌开始,看看新的一张牌和旧牌相比的大小,然后把新牌插到合适的地方。也就是说,插到一个左边的牌比它小,右边的牌比它大或者一样大的地方。如果这张新牌比手里所有的牌都小,那就把它放到最左边;如果这张新牌比手里所有的牌都大,那就把它放到最右边。
恭喜你,你已经完成了第一个排序算法,叫作 插入排序算法 (insertion sort)。这个办法可以保证你在抓牌的过程中,总能把所有的牌都从小到大排好。
计算机常用插入排序算法来维持一批有序的物件。比如,来了一件新商品,计算机可以用插入排序算法把它插到原来的商品清单里,保持所有商品的顺序。理论上,把任何新的物品,无论是商品、网页、歌、视频还是账号,加到原有的已经排好的清单中,计算机都可以用插入排序算法,不过这不一定是最好最快的方法罢了。
你现在已经了解了第一个算法——插入排序算法,我们来更清楚地解释一下什么是“算法”。算法是一个方法,它包含一系列具体的指令,去解决一个问题或者完成一个任务。你可以看到,对算法的解释一定要足够清晰,没有歧义,这样接受方看到以后才会知道怎么做。也就是说,上面所说的抓牌的方法是一个算法,任何一个人或者计算机都可以遵从这些指示,把一组牌按照顺序从小到大排好。在后面的章节中,你会看到很多算法的例子,我也会越来越多地介绍算法的特性。

下面请思考两个相关的小问题:
(1)如果我们希望牌是从大到小进行排序,那上面同样的方法可以用吗?
(2)上面这个抓牌的方法,和一共有几张牌相关吗?也就是说,对1张牌、5张牌、100张牌来说,这个方法都会管用吗?
下一节,我将用孩子排队来解释另外几种常用的排序算法,然后你会看到,这些算法不仅可以用于孩子排队,还可以用于本章开头讲述的任何排序场景。
开学的时候,一群不认识的同学来到一起,需要从矮到高排队。下面我们来仔细地分解一下,如果让一台计算机来做这件事,它可以怎么做。记住,计算机做这件事,不能只是说“你们排队吧”,它必须有确定的一步步的方法。
我们分析一下几种常用的方法,来介绍几种不同的排序算法。
第一个方法:计算机先找到最矮的同学,让他站在最前面,然后,再从余下的同学中找最矮的,排在第一个后面,以此类推,直到把所有同学排好,如图2-4所示。
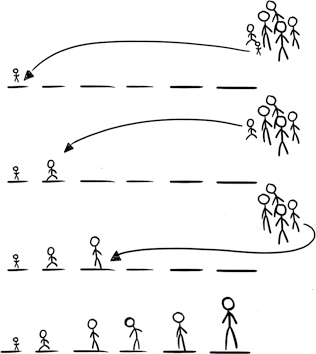
图2-4
这个方法就是经典的计算机 选择排序算法 (selection sort),也就是每次都选一个最矮的。你可以想象,计算机可以把每个同学的身高表示成一个数字,每次看所有的数字,挑一个最小的,放到一边,然后再从剩余的数字里面挑最小的,直到把全部数字都按从小到大的顺序排好。这个方法的好处是简单易懂,缺点是比较慢,计算机每次都要在没排过的所有数字当中看一遍,挑一个,每次都要看剩下的所有同学谁最矮。
我们再来看第二个排序的方法:所有的同学先随便站成前后一排,然后,前后相邻的两个同学互相看一下对方,如果前面的比后面的高,那他们就换一下位置。
这个方法是不是比较有趣?你是不是相信,用这个方法最后也能把同学们从矮到高排成一排?
下面我们来展示一下3个同学用这个方法的排序过程。假设3个同学的代号分别是1,2,3。1比2矮,2比3矮。开始这3个同学的顺序是3,1,2。那么第一次,3和1交换,变成1,3,2;第二次,再把3和2交换,变成1,2,3,排序就完成了,如图2-5所示。
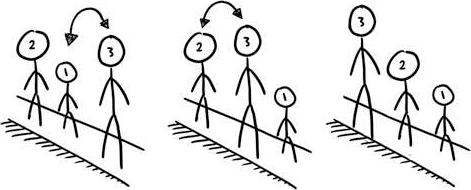
图2-5
假设开始这3个同学的顺序是2,3,1,那么第一次,3和1交换,变成2,1,3;第二次,再把2和1交换,变成1,2,3,排序也就完成了,如图2-6所示。
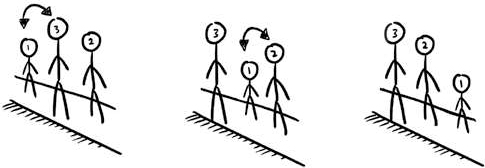
图2-6
为了方便理解这个方法,你可以用几张卡片来试一下。给卡片写上1,2,3等数字,代表从矮到高的同学。然后,随便它们开始怎么排,用两两交换的办法,几步后你就可以把整个顺序排好。
你可以试试其他组合,是不是无论开始的时候是“3,2,1”,“2,1,3”或者“3,1,2”,都能排成1,2,3?也许你已经发现了,是不是有的时候比较快,只要交换一次,而有时候要多交换几次,慢一点?
这里我们要强调,虽然我们举的例子只有3个同学,但是这个方法是在任何数量的情况下都奏效的,不管是几十个、几百个还是几万个。这个交换的算法是另一个经典排序算法,叫 冒泡排 序算法 (bubble sort)。如图2-7所示,你可以想象最矮的孩子像气泡一样,一步步从他的位置移到队伍的第一位。

图2-7
我再问你一个问题:用这个方法,什么时候能知道每个人都排好了,不用再排了?你可能会发现,当队伍里面每个后面的人都比前面一个人高,不用再换位置,这个过程就可以结束了。
你可能要问,为什么要用第二个方法呢?用方法一,老师直接选择排不是挺好的吗?原因是如果只有10个同学,我们当然可以用方法一来排。但如果有1万个同学排队呢?那用方法一就太难了,老师第一次要在1万个同学里挑最矮的,第二次要在9 999个同学里面挑。而方法二,每次都是前后两个人交换,就不会太难。方法二还有一个特别大的好处,就是可以同时进行:前后两个同学随时都可以交换,不用等老师一个一个看。这就是前面第1章提过的并行处理,而计算机做并行处理是很在行的。
你可能还会问,为什么要把1万个同学从矮排到高啊?其实,孩子排队只是个比喻,这1万个孩子可以是1万个网页、视频、商品。我前面就说过,计算机要处理的问题并不是3个孩子排序这样简单的小问题,而是很多的东西,比如成千上万个商品,成千上万个短视频,要不断排序的那个更大的问题。你只要理解了这个方法,它在数目很大的情况下还是会奏效的。
有趣的排序方法很多,我再给大家提供一个方法三:男孩从矮到高排好队,女孩从矮到高排好队,然后老师站在前面,每次老师从两个队的队首挑选出比较矮的孩子,依次合成一个队就行了。这个算法叫 归并排序算法 (merge sort)。
图2-8示意了一个简单的归并排序过程。在这个情景中,一共有3个男孩a、b、c和2个女孩x、y,他们都已经从矮到高排好。在下面的5步当中,每次最矮的男孩和最矮的女孩进行比较,第一次a被选中,第二次b被选中,第三次x被选中,第四次c被选中,第五次y被选中。这样比较5次,5个孩子就都排好了。
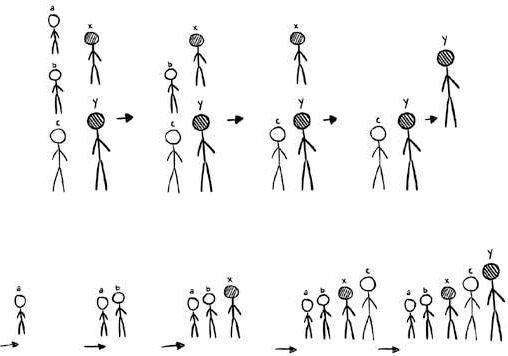
图2-8
方法三看上去很简单,但是它有个要求,就是男孩、女孩要先分别排好。仔细想一下,归并排序其实使用了问题分解的方法,把排一个大队的问题,分成了先排两个小队,再把小队合成一个大队的问题。小队人少,好排,小队合成大队又很简单。这里,我们可以看到计算思维在起作用。

下面请思考两个相关的小问题:
(1)一个年级有5个班,现在要按身高给所有学生排队。假设每个班的同学可以先排好,你是否可以用归并排序算法把所有同学排好?怎么做?
(2)一个年级有5个班,现在要按身高给所有学生排队。你是否可以先用一种算法把每个班的学生排好,然后再把全体学生排好?怎么做?与所有学生一起用一个算法相比,这样做的好处和坏处是什么?
前面讲的每一个排序的方法,在计算机术语里都叫算法。算法就是用一系列简单确定的操作来完成一项标准任务。算法是计算机用来解决问题的基本单元。因为计算机是一台机器,它不会猜想,也没有直觉或者感情,算法的操作必须是清楚的,没有歧义的,可以严格遵从的。
算法的第一个重要特性是 正确性 ,也就是它在任何情况下都必须正确。例如,我们如果用某个算法为孩子排队,那么不管是对1个孩子,10个孩子,还是100万个孩子,也不管他们开始是怎么站的,这个算法都要保证最终能够把所有的孩子排好。算法系统地解决一类问题,而不是解决某个特殊的问题。这是算法的强大之处。对于前面介绍的几个算法,虽然在这里我们没有严格地证明,但是它们都是被验证正确的。
同时,大家在排序的例子里还可以看到很多计算机算法的其他特性,比如多样性、重复性、完整性。
多样性。对同一个问题的解法有多个,每个方法在不同的情况下可能效果很不一样,有的在这种情况下解得快,有的在那种情况下解得快。往往总有一个很笨的方法能达到目的,比如一个个地数过挑人。计算机可以先用这个笨算法,然后再改进。也就是说,虽然每个算法是确定的,但每个问题都可以用多种不同的算法来解。
重复性。大家可以注意到一个现象,我们经常有一些事情需要重复地做,直到某一个条件被满足为止。比如说,重复直到所有的孩子都排好了。条件满足了,算法就结束了。这里讲了一个计算里常用的概念,叫循环,就是一件事情需要反复地做,直到某一个条件被满足为止。计算机最擅长不厌其烦地重复劳动。这个概念之所以重要,是因为有了这个循环条件,这个算法可以被用在N多个孩子排队上,不需要预先知道一共有多少个孩子。
完整性。排队不能有的孩子没排进去,所以我们的方法要保证把每个孩子都排好。比如有3个孩子一样高,排序算法需要正确地工作,不能一直犹豫谁排在谁前面,也不能扔掉2个孩子。或者说,假设一共有10个孩子,把8个排好也是正确的,但这是不完整的。其实,这个完整性也是正确性的一个角度,我们把它单独提出来,是因为仅仅有正确的结果还是不够的。
到了这里,看了这些,你是不是觉得计算思维和数学思维不是一回事了?
我们学习排序的目的,不是要认出哪个孩子高,哪个数更大,而是要知道怎么样正确地把一个队排好。计算思维更关心在不同的初始情况下,具体的一步步的方法是怎样的,这样我们就可以写程序让计算机操作。换句话说,计算机关心的是如何做事。另外,因为计算机要解决大的问题,所以计算思维也会关心在数目很大的情况下,哪一个方法才是最快的。
算法一旦被表示清楚,不同的计算机执行同一个算法,每次都可以产生同样的效果。就好比任何人拿了那个炒鸡蛋的菜谱,只要严格按照那个菜谱做,他总是能够把鸡蛋炒熟。算法也是一样,不管哪个老师按照我们这个小孩排序的算法做,他总是可以正确地把学生排出来的,排的中间过程也一样,不会因为不同的老师操作而不同。搜索的结果,商品的推荐名单,都不会因为是不同的电脑来操作而有所不同。
还有非常重要的一点,就是你会发现,不管我们是排简单的数字1、2、3,还是孩子的身高1.5米、1.6米,还是按字母顺序从A排到Z,只要我们排序的那个东西可以比出大小或者先后,这些算法都是奏效的。这是个 抽象 的概念,也就是说我们其实可以不去关心具体排的是什么东西,不关心数字有没有小数点。我们可以抽象地用简单的数字1、2、3去说明和学习这些算法,知道它们也适用于非简单数字的其他场景。
比如,我们说过抖音算法的最后一步是排序。在这个时候,也就是第1章图1-7的3.2步,每个视频都已经和你的个人喜好匹配出一个分数,比如视频1是5.0分,我们表示为(视频1,5.0)。其他的视频和分数是(视频2,6.6),(视频3,4.3),(视频4,8.9),(视频5,3.1)。我们可以用选择排序算法,或者冒泡排序算法,把这5个视频按照分数从高到低排列:
(视频4,8.9)
(视频2,6.6)
(视频1,5.0)
(视频3,4.3)
(视频5,3.1)
排好以后,这些视频就可以按照这个顺序展示给你看了。也就是说,你刷抖音的时候它按照你的喜好把视频推荐给你。这个时候,如果有新的视频到来,抖音可以用插入排序算法把新的视频插到未看视频队列中合适的地方,这样任何时候你看到的都是和你的喜好最相关、最匹配的视频。
我们怎么把学到的分解问题和排序算法连起来用呢?举个例子,我有一次去广西支教,给孩子们发冬衣,去之前要统计孩子的身高,到时候要把衣服按大小排好在操场上,然后给孩子们排队,让他们认领。这里有一个有趣的问题:如果有1万个孩子,1万件大小不同的衣服,怎么把合适的衣服发给合适的人呢?
这个答案就是我们分发衣服的三步:
(1)把人从矮到高排好。
(2)把衣服从小到大排好。
(3)按顺序给每人发1件衣服。
以上这三步可以用一个串联的流程图来表示(见图2-9)。

图2-9
后面我们会遇到不少算法,它们都有多个步骤。从现在开始,我们把算法写成下面这个方式:每一行代表做事的顺序,也就是说,我们不再具体写出“第一步”“第二步”“第三步”。每一行,我们叫一个 指令 ,一般是指向一件清楚的可以具体操作的事。我们假设这些指令会按照顺序一行一行串行地执行,和流程图表示的一样。对于下面这个算法,我们在右面标出了指令1、2、3,如果没有标出,你也可以认为是从上到下一行行地执行。

你发现了吗?当我们解决这个发衣服问题的时候,第一步和第二步都是排序,可以用我们刚刚学到的排序算法来做。在思考怎样发衣服的时候,我们不需要具体思考这两个关于排序的子问题怎么解决。也就是说,上面说的第一步和第二步可以先不考虑。我们可以假设,总有办法能把人和衣服分别排好,我们把排序问题外包,再“调用”就行了。我们刚刚学过的排序算法给了我们自信。而且你会发现,排人和排衣服可以用不同的排序算法,比如人可以让他们用互换法自己排(冒泡排序),衣服可以按号码的大小排(选择排序)。图2-10展示了这两种不同的算法。

图2-10
这种思维把大问题(分配衣服)分解成子问题(两个排序加一个匹配),并且假设子问题(排序)已经有现成的解,只要调用它们就行了。这是我在第1章所讲的分解问题和本章所讲的算法的结合,也是计算思维的精髓所在。
另外,你可能已经发现了,1万个人排序和1万件衣服排序是可以同时进行的!这两个排序只要在发衣服之前都做好就行了(见图2-11)。可以想象,给1万个人或物品排序要花很长时间。让这两个耗时的任务同时做,总体上所需的时间就会短多了。如果给1万个人排序要10个小时,给1万件衣服排序要5个小时,给所有人发衣服要2个小时。那么串行的算法(见图2-9)需要10+5+2=17个小时,而并行算法(见图2-11)只需要10+2=12个小时。
图2-11
你也许在想,怎么会给1万个人发衣服呢?记住,这些例子都只是为了解释算法的概念。一旦我们懂得如何操作,这些算法可以有特别多的应用。
比如,上面发衣服的算法,在我们的工作和生活中类似场景很多,只不过你可能还没意识到,这些都是排序问题。我再举一个例子。“6·18”购物节快到了,假设中国移动要做“积分送好礼”活动,给积分最高的1万个用户送上金额不等的免费话费礼券。它的算法用流程图表现出来如图2-12所示。
图2-12
你可以看到,这个算法和发衣服的算法是一模一样的。用户按积分高低排序,礼券按金额大小排序,都可以用我们已经学过的排序算法来排。在中国移动“积分送好礼”这样的大型实际应用中,常常要给这样大数目的人和物排序。而我们学到的这些约定俗成的排序算法,都是计算机专家已经证明正确的方法,都可以直接拿来用。

图2-13
下面我们来看一个有一定空间限制的排序。小明需要把9个乱的数字按大小排好。我们列出,这9个数开始的时候是这样的:7,8,2,9,5,1,8,5,3。可是,小明能力有限,每次只会排6个数字,再多他就想不清楚了。那他怎么排9个数呢?小明可以像下面这样做。
(1)排前面6个数,成为: 1,2,5,7,8,9 ,8,5,3。
(2)排后面6个数,成为:1,2,5, 3,5,7,8,8,9 。
(3)再排前面6个数,成为: 1,2,3,5,5,7 ,8,8,9。
这时候小明看了一下,后面6个数也已经排好了。他就停下来,宣布9个数全部都排好了。
小明的算法是:先用学过的任何方法排前面6个数,再排后面6个数,如此反复循环,直到前面和后面的6个数都已经排好了,也就是说,再没有需要移动的数字了,他就宣布排序成功。
可以说,小明虽然每次只能排6个数,但他还是相当聪明的。他的方法可以保证这串数的前半部分和后半部分都是排好的,中间又有衔接,他的确可以保证这串数字都排好了。

下面请思考两个相关的小问题:
(1)我们说小明停止他的算法时,他的9个数都已经排好了,为什么?如果这9个数还有顺序颠倒的,他是否会停下来?换句话说,如果这9个数还有顺序颠倒的,那么他的前6个数或者后6个数是否还有更多排序工作要做?
(2)如果有一串很长的数,比如1万个,小明每次排6个,保证每6个数有重叠(比如1~6号数字,6~11号数字,11~16号数字等),他的这个方法还有效吗?
计算机有时候也会遇到小明这种情况。比如要排50亿个网页,计算机可能一次也排不出来,没那么大的空间,所以前面提到的开学排队的算法不能直接用,计算机需要像小明一样,一部分一部分地排,再衔接起来。对每一部分,计算机都可以使用我在前面介绍的经典排序算法。
总结一下,很多强大的应用都会用到排序。
● 短视频App展示的是按照你的喜好排好的视频清单。
● 电商网站展示的是按照销量、评价、价格等排序的商品。
● 搜索的结果是按相关性排序的网页。
● 通信录是按照名字排好的联系人。
● 银行账单是按照时间排序的交易清单。
● 流行歌单是按播放量来排序的歌曲。
排序是很多计算机算法的基础,也是了解计算机必须迈出的第一步。计算机科学家发明的排序算法远远多于上面介绍的几种,每一种都适用于不同的情况。有的算法内部很复杂,比如基于机器学习的商品推荐系统,会按照它猜测你可能想要购买的商品给你推荐,而不是简单地排序。但是,不管算法内部多么花哨和复杂,结果都是一个有序列的清单。
根据事情的优先级给我们生活中每一天要做的事情排序,可以大大提高我们时间管理的效率。下面用艾维·利时间管理法来举一个具体的例子。
伯利恒钢铁公司总裁舒瓦普曾会见效率专家艾维,艾维说能帮舒瓦普把他的钢铁公司管理得更好。舒瓦普承认自己的公司不尽如人意,可是他说自己需要的不是更多知识,而是更多行动:“应该做什么,我们自己是清楚的。如果艾维你能告诉我们如何更好地执行计划,我就听你的,在合理范围内价钱由你定。”
艾维递来一张白纸,请舒瓦普在这张纸上写下明天要做的6件重要的事:“现在,用数字标明每件事对于你和公司的重要性的次序。”
艾维接着说:“现在把纸放进口袋,明天早上拿出来,做第一件事。不要看其他的,只看第一项,着手办第一件事,直至完成为止;然后用同样方法对待第二项、第三项……直到你下班为止。如果你只做完第一件事,无所谓,因为你是在做最重要的事情,一切都值得!”
艾维说:“每一天都要这样做。在你对该方法的价值深信不疑后,叫公司的其他人也这样干。如果能带来价值,请给我寄来支票,值多少就给我多少。”
几个星期后,舒瓦普寄去一张2.5万美元的支票和一封信,信上说,从钱的方面看,那是他一生中最有价值的一课。5年后,舒瓦普的小钢铁厂从5年前名不见经传的小厂跃居为世界最大的独立钢厂,而艾维推荐的时间管理方法已为舒瓦普赚得了1亿美元。
我们来总结一下艾维·利时间管理法的具体步骤:
(1)写下你明天要做的6件最重要的事。
(2)用数字标明每件事的重要性次序。
(3)明天早上第一件事是做第一项,直至完成或达到要求。
(4)然后再开始完成第二项、第三项……
(5)每天都要这样做,养成习惯。
这其中,第二步,也就是排序,是最重要的,它帮助人们遵从两个重要原则:(1)先解决最重要的问题,(2)每次只解决一个问题。
我们在生活中常常看不清楚的优先级问题,比如工作和生活的平衡,该去同学聚会还是在家里看书,都是没有想清楚要按什么来排,什么对你最重要。每天的时间对于每个人都一样多,用排序思维来管理时间可以让你的每一天更高效。
从古至今,人们每天都在执行着各种算法,只不过在今天看到这一章的内容之前,你不一定这样想。
“sort”这个英文单词,不仅仅用于排序和分类东西,也有“整理、应付、搞定”的意思。一个场景被“sort out”,就是排整齐了,也可以说是搞清楚了。生活中的矛盾混乱,往往源于一个优先级的问题。排序最关键的是要知道按照什么排,比如商品是按价格、销量还是评分来排,你的朋友是按亲密程度、交往时间还是有用程度来排。如果我们想清楚了,知道是按照自己最在意的标准来排序,我们就头脑清晰,能分辨出哪一个是主要的,哪一个是次要的。这样我们就可以先做主要的事情,先做高价值的事情。
算法、排序算法、插入排序算法、选择排序算法、冒泡排序算法、归并排序算法、抽象、指令。
◆ 算法是一个方法,它包含一系列具体的指令,去解决一个问题或者完成一个任务。对算法的解释一定要足够清晰,没有歧义,任何人拿同样一个算法去做事,做出来的结果都是一样的。
◆ 算法系统地解决一类问题,而不是解决某个特殊的问题。这是算法的强大之处。无论是1个、10个,还是100万个事项,算法的应对在任何情况下都保证是正确的。
◆ 对同一个问题,往往有多个算法可以解。计算思维关心的是哪个解更快、更好,或者说效率更高。
◆ 看似很复杂的问题,比如抖音的推荐,拆解之后也会变成我们已知的算法可以解的问题,比如这是个排序的问题。
“为什么一只乌鸦像一张写字桌?”帽匠问。
“好了,现在我们有有趣的事做了!”爱丽丝想。
“真高兴他们开始出谜语了。我一定能猜出来。”她大声地说。
“你的意思是你能猜出答案?”三月兔问。
“正是这样。”爱丽丝说。
——刘易斯·卡洛尔《爱丽丝漫游奇境记》
“Why is a raven like a writing-desk? ” The Hatter said.
“Come, we shall have some fun now! ” thought Alice.
“I'm glad they've begun asking riddles. — I believe I can guess that. ” she added aloud.
“Do you mean that you think you can find out the answer to it? ” said the March Hare.“Exactly so. ” said Alice.
— Lewis Carroll, Alice in Wonderland