1.14　超对称性

到此为止，我一直放肆地无视了超对称的关键问题，虽然超对称让格林和施瓦玆将弦论时空的维度从26减到10，而且还在弦论里扮演着很多其他基本角色。实际上，超对称概念的重要是在远离弦论的物理考虑中发现的。的确，我们可以认为超对称是现代物理学的一个时髦概念，那么它本来就值得在本章里认真考虑！尽管这个概念的很多动力确实来自弦论的需求，它的时尚地位在很大程度上却独立于弦论。

什么是超对称呢？为了解释这个概念，我们要回到1.3和1.6节关于物理学基本粒子的讨论。回想一下，存在不同的有质量粒子族，如轻子和强子；还有其他粒子，如无质量的光子。其实还有更基本的粒子分类，只分两类，比前面遇到的分类便捷多了。如1.6节说的，粒子被简单分为费米子和玻色子。

表示费米子与玻色子区别的一种方法是，认为费米子更像我们从经典物理认识的粒子（电子、质子、中子等），而玻色子像粒子间的力的携带者（光子是电磁力的携带者，W和Z玻色子是弱相互作用的携带者，而所谓 胶子 则是强相互作用的携带者）。然而这并非泾渭分明的区别，特别因为还存在类似粒子一样的π子、K子和1.3节的其他玻色子。而且，有些类粒子原子可以很好地近似认为是玻色子，其组成部分在很多方面都像单个粒子。玻色子与费米子没那么大的区别，两者都像经典粒子。

不过我们暂且不管复合粒子的问题，也不管它们是否可以合理地当单粒子来处理。迄今我们所考虑的客体都可以作为单粒子，费米子与玻色子之所以显现区别，是因为所谓的泡利 不相容原理 ，它只适用于费米子，告诉我们两个费米子不可能同时处于相同状态，而两个玻色子可以。大致说来，泡利原理断言两个全同费米子不可能一直相互重叠，它们仿佛心有灵犀，靠得太近时就会相互推开。另一方面，玻色子对与它同类的粒子有着某种亲和力，能一直重叠在一起（如著名的 玻色 — 爱因斯坦凝聚态 就是多个玻色子聚在一起的状态）。这些凝聚态的一个解释，见［Ketterle 2002］；更一般的文献，见［Ford 2013］。

稍后我还会回到量子力学粒子的这相当怪异的一面，力图说明那相当模糊的特征，这当然只是为我们提供一幅玻色子与费米子差异的不完整图像。更清楚的区别来自粒子自旋速率的考察。奇怪的是，任意（非激发）量子粒子的自旋有确定而固定的量，正好成为粒子特殊类型的表征。我们不要把这个自旋看成角速度，而要看成角动量——在无外力作用下运动的物体所拥有的一种特殊自旋度量，在物体的整个运动中保持不变。想象一只在空中旋转着运动的棒球或板球，或者立在一只冰鞋上旋转的溜冰者。在这些情形，旋转在角动量意义上是保持不变的，而且在没有外力（如摩擦力）的情况下会永远保持下去。

溜冰者的例子也许更恰当，因为我们能看见角速度在溜冰者双臂展开时变小而在双臂收紧时变大。在这个过程中保持不变的是角动量，角速度一定时，物质分布（如溜冰者双臂）距离旋转轴越远，角动量越大，物质分布距离旋转轴越近，角动量越小（图1.36）。所以，为了维持角动量保持不变，手臂的收缩必须由旋转速度的增大来弥补。

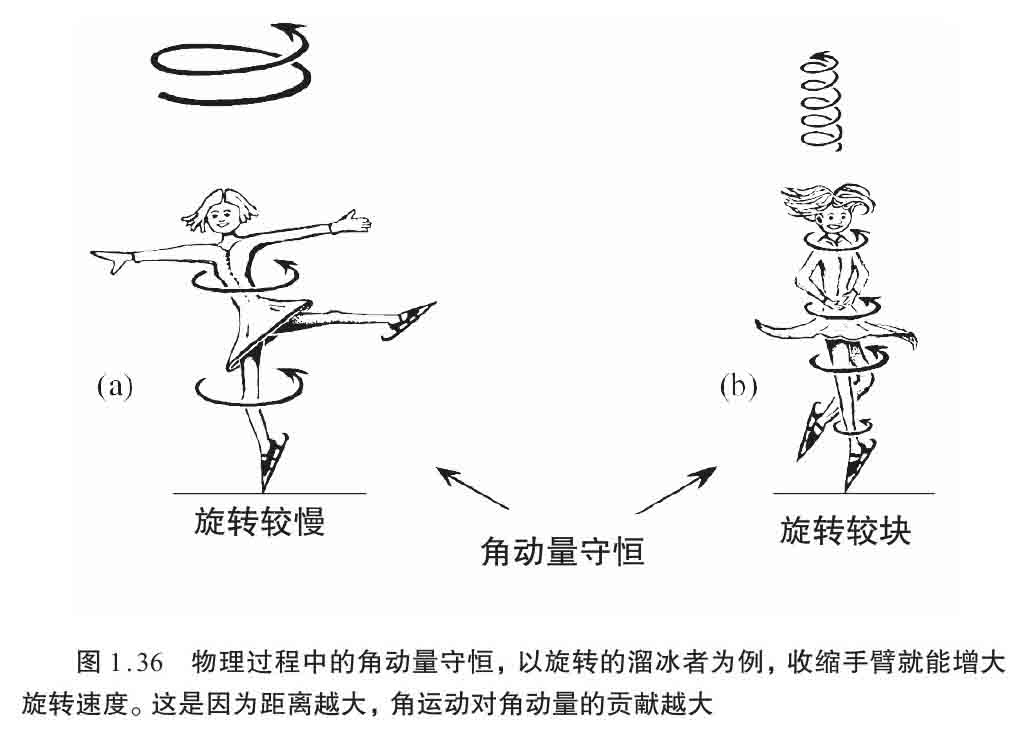
这样，我们有了一个对所有密实孤立物体都适用的角动量概念，它也适用于单个量子粒子。但量子水平的法则有些奇怪，需要费点儿工夫才能习惯。我们发现，就单个量子粒子而言，每个类型的粒子，不论处于什么情形，其角动量的数量总是同一个固定的数。在不同情形下，自旋轴的方向倒不一定总是相同，但自旋方向以一种奇异的、根本上是量子力学的方式表现出来，我们将在2.9节探讨。就眼下说，我们只需要知道，如果想看看粒子自旋有多少分布在某个特定的方向，那么对玻色子来说，其数值等于 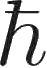的整数倍—— 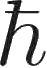是狄拉克约化的普朗克常量 h （见2.11节），即

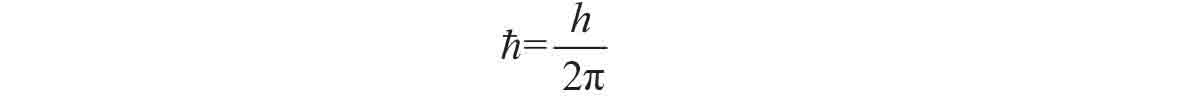
这样，玻色子在任意方向的自旋值必然等于下列数值之一：

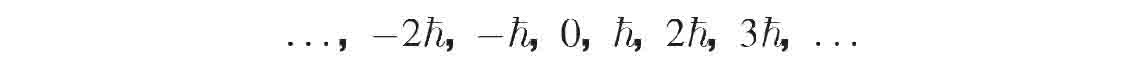
然而在费米子情形，任意方向的自旋值与它们相差 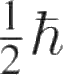，即取如下值：

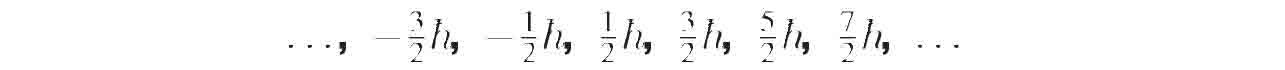
（即数值总是 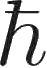的半奇数倍。）我们将在2.9节更详尽地看到如此奇异的量子力学特征是如何表现的。

在QFT框架下证明过一个著名的定理，叫 自旋统计定理 ［Streater and Wightman 2000］，大概意思是说玻色子/费米子区别的这两种观点是等价的。更精确地说，定理得到了一个在数学上比前面所说的泡利不相容原理更加深广的新的法则，即玻色子和费米子都必须遵从的一种统计。要圆满解释这个定理，需要进一步深入量子力学的数学形式，这超出了本章的范围，但我还是想传达一些它所蕴含的基本东西。

回想1.4节（也见2.3～2.9节）的量子振幅，人们期待在QFT计算中获得那些复数（见1.5节），由此得到量子测量的概率（根据2.8节的玻恩法则）。在任意量子过程中，那个振幅应该是描述过程所涉全部量子粒子的参数的函数。我们也可以认为振幅是我们将在2.5～2.7节考虑的薛定谔波函数的值。假如P 1 和P 2 是过程中的两个全同粒子，则振幅（或波函数） ψ 是两个粒子各自的参数组 Z 1 ， Z 2 的函数 ψ （ Z 1 ， Z 2 ）（这里我用单个的黑体字母 Z 来包括各粒子的所有参数：位置坐标或动量坐标，自旋值，等等）。下标的选择（1或2）指粒子的选择。对 n 个粒子P 1， P 2 ，P 3 ，…，P n （全同或不同），我们有 n 个这样的参数组 Z 1 ， Z 2 ， Z 3 ，…， Z n 。于是有所有这些变量的函数 ψ

ψ = ψ （ Z 1 ， Z 2 ，…， Z n ）

现在，假如 Z 1 描述的那类粒子与 Z 2 描述的相同，且为玻色子，则我们总会发现对称性

ψ （ Z 1 ， Z 2 ，…）= ψ （ Z 2 ， Z 1 ，…）

于是交换粒子P 1 和P 2 不会影响振幅（或波函数）。但是假如粒子类型（ Z 1 与 Z 2 相同）为费米子，则我们发现

ψ （ Z 1 ， Z 2 ，…）=- ψ （ Z 2 ， Z 1 ，…），

则交换P 1 和P 2 会改变振幅（或波函数）的符号。我们可以注意到，假如P 1 和P 2 的每个粒子都处于彼此相同的状态，则 Z 1 = Z 2 ，从而必然有 ψ =0（因为 ψ 等于其负）。根据玻恩法则（1.4节），我们看到 ψ =0意味着零概率。这表述了我们不能发现两个全同粒子处于同一状态的泡利原理。假如所有 n 个粒子都全同，则对 n 个玻色子，我们可将对称性推广到交换任意一对粒子：

ψ （…， Z i ，…， Z j ，…）= ψ （…， Z j ，…， Z i ，…）

而对费米子，有任意粒子对的反对称性：

ψ （…， Z i ，…， Z j ，…）=- ψ （…， Z j ，…， Z i ，…）

以上两个方程分别表达的对称性和反对称性是区别玻色统计与费米统计的基础。当我们“数”涉及大量同类玻色子的不同状态数时，不用考虑交换一对玻色子时达到的新态。这个计数方法生成所谓的 玻色 — 爱因斯坦统计 （或 玻色统计 ，这也是玻色子名称的由来）。这对费米子也成立，只是要改变振幅符号，由此产生 费米 — 狄拉克统计 （或 费米统计 ，这是费米子的由来），它有很多量子力学涵义，其最显著者就是泡利原理。我们注意，不论玻色子还是费米子，两个同类粒子的交换都不会影响量子态（只不过是改变波函数的符号，这不会改变物理状态，因为乘以-1只是改变相因子的一个例子：×e iθ ，这里 θ = π，见1.8节）。相应地，量子力学确实要求两个同类粒子必须是完全相同的！这说明了爱因斯坦对外尔的规范理论的反驳是多么重要——在他的建议中，“规范”实际上指的是尺度的变化，见1.8节。

这就是标准的量子力学，它有大量观测支持的卓越结果。然而很多物理学家相信，应该存在一种新的对称性，将玻色子族和费米子族相互转换，犹如那些将轻子相互联系起来从而生成弱相互作用规范理论的对称性，或者那些联系不同夸克从而生成强相互作用规范理论的对称性（见1.3节和1.8节末段）。因为两族粒子遵从的不同统计，这种新对称性不可能是普通对称性。相应地，不同物理学家将寻常类型对称性推广为一种新对称性，叫 超对称性 ［Kane and Shifman 2000］，它将玻色子的对称态转换为费米子的反对称态，反之亦然。其中还引入了几种奇怪的“数”——叫超对称生成元——其性质是，当你把两个生成元相乘时，如 α 乘以 β ，会得到它们的相反次序的乘积的负数：

αβ = - βα

（其实，算子的不可交换性，即 AB ≠ BA ，在量子形式下是很普通的，见2.13节。）正是这个负号能将玻色—爱因斯坦统计转换为费米—狄拉克统计，或者相反。

为更精确说明这些非对易量，我要多说几句量子力学（和QFT）的一般形式。在1.4节，我们遇到过系统的量子态的概念，如态（ ψ ， Φ 等）遵从复矢量空间的法则（A3和A9节）。以后我们会看到（特别是1.16，2.12，2.13和4.1节），在所谓线性算子的理论中，有几个重要角色。作用于 ψ ， Φ 等量子态的算子 Q ，以其保持量子叠加的事实为特征：

Q （ w ψ + z Φ ）= w Q （ ψ ）+ z Q （ Φ ）

其中 w 和 z 为（常）复数。量子算子的例子有位置和动量算子 x 和 p ，还有我们将在2.13节遇到的能量算子 E 和2.12节的自旋算子。在标准的量子力学中， 测量 通常用线性算子来表示，这一点将在2.8节说明。

在超对称算子如 α 和 β 的情形，它们也是线性算子，但在QFT的作用却是施加于其他线性算子，叫 生成 和 湮灭 算子，是QFT代数结构的核心。湮灭算子可以用符号 a 表示，则 a + 代表对应的生成算子。假如我们有一个特殊量子态 ψ ，那么 a + ψ 就是通过加入由 a + 代表的特殊粒子态而从 ψ 获得的一个态；类似地， aψ 是通过从 ψ 消减这个特殊粒子态而获得的一个态（假定如此消减是可能操作；否则我们只能得到 aψ = 0 ）。接下来，超对称算子 α 将作用于玻色子的生成（或湮灭）算子，将其转换为相应的费米子算子，反之亦然。

注意，在关系 αβ = - βα 中选择 β = α ，我们得到 α 2 =0（因为 α 2 等于其负值）。由此，我们不可能得到任何高于1阶的超对称算子。这导致一个奇怪的结果：假如我们总共只有有限个超对称算子 a ， β ，…， ω ，则任意代数表示 X 不用这些量的幂就能写出来：

X = X 0 + α X 1 + β X 2 +…+ ω X N + αβ X 1 2 +…+ αω X 1N +…+ αβ … ω X 1 2… N

于是求和有2 N 项（每个可能的不同数目的超对称算子的集合都有一项来代表）。这个表示确定地说明了对可能出现的超对称算子的唯一一种依赖性——尽管右边的有些项可能为零。第一项 X 0 有时被称为 体 ，其余项 α X 1 +…+ αβ … ω X 12 ... N （其中至少出现一个超对称算子）则为 心 。注意，只要表达式的某个部分进入心，则它乘以其他这样的表达式是永远不会回到体的。于是，任何代数计算的体代表了其自身，它为我们提供了完全合法的 经典 计算，这里我们可以干净地忘却心的部分。这为代数和几何考虑赋予了合法的角色，就像1.11节的讨论一样，在那儿完全忽略了超对称性。

超对称性的要求为物理理论的选择提供了一个指南，理论必须满足超对称性，这实际上是一个很强力的限制，它为理论在玻色子和费米子部分之间赋予了一定的平衡，让两个部分通过超对称操作（即借助如以上 X 那样的超对称算子构造的操作）相互联系。在旨在以合理方式模拟自然的QFT的构造中，这被认为是很有价值的工具，这样可以免受不可控的发散的痛苦。超对称的要求极大提高了理论可重正化的机会（见1.5节），也大大增强了它为重要物理问题提供有限答案的能力。有了超对称性，源自理论的玻色子和费米子部分的发散其实就相互抵消了。

这大概就是超对称在粒子物理学流行的主要原因之一（除了弦论）。然而，假如大自然真是完全超对称的（例如有 一个 超对称生成元），则任何基本粒子都将伴随着另一个——叫 超对称伙伴 ——与原来那个有着相同的质量，那么每对超对称伙伴都由一个玻色子和一个相同质量的费米子构成。这就必将存在 一个超电子 ，即伴随电子的玻色子；也将有伴随每类夸克的玻色型的 超夸克 、还将有无质量的 光微子 和 引力微子 ，即伴随光子和引力子的费米子。另外还将有伴随前面提过的W和Z玻色子的W 微子 和Z 微子 。实际上，整个情形比这些相对简单的一个超对称生成元的情形要惊人得多。假如有 N 个超对称生成元（ N ＞1），基本粒子将不仅仅以这种方式成对出现，每个超对称群组（多重态）还会有2 N 个相互伙伴，一半玻色子、一半费米子，且具有相同的质量。

看到基本粒子的如此惊人的繁衍特征（或许“基本粒子”这个名词都有点儿荒谬），读者若是听说还没见过这种超对称粒子群，大概会长舒一口气吧！不过，观测事实并没阻碍超对称的支持者们。正如人们通常论证的，总会存在某些超对称破缺的机制，导致本来对在自然中实际观测到的粒子成立的精确超对称性出现严重的偏离，从而任何多重态中的粒子质量实际上悬殊很大。于是，所有这些超对称伙伴（每组粒子中迄今观测到的单个数量的伙伴）都将具有超出目前投入运行的粒子加速器能力的质量！

当然，超对称预言的粒子仍然有可能确实存在着，只是因为它们质量太大我们才没观测到。人们曾寄望于LHC（大型强子对撞机）重新全力投入运行后，能在更高能量水平上提供支持或反对超对称性的明确证据。然而，超对称理论有许多不同纲领，在超对称破缺机制所要求的能量水平和性质问题上众说纷纭。在我写作本书时，还没有显现超对称伙伴的任何证据，不过这还是有点儿远离大多数科学家为之奋斗的科学理念，即一个理论纲领要成为真正科学的［至少依据科学哲学家波普尔（Karl Popper ）［1963］的著名准则］，那它应该是 可证伪 的。我们有一种不安的感觉，即使超对称作为自然的一个特征是真的错了，LHC或任何后来更强大加速器也没发现任何超对称伙伴，超对称的某些支持者也可能得出结论说，超对称的错 不是 因为自然的真实粒子，而只是超对称破缺的水平高于当时所能达到的水平，因此还需要更强大的机器去观测它！

其实，就科学的可反驳性而言，情势可能没那么坏。LHC的最新结果，包括长久追寻的希格斯玻色子的发现，不仅没找到任何已知粒子的超对称伙伴的证据，实际上还否决了最直接且曾被寄予厚望的超对称模型。理论与观测的约束可能对迄今提出的那类超对称理论的任何合理形式都有着重大意义，能将理论家们引向更新也更有希望的玻色子族与费米子族相互作用的思想。我们也应该指出，那些有多于一个超对称生成元的模型——如理论家中间十分流行的4生成元理论（叫 N = 4 超对称杨 — 米尔斯理论 ）——比任何单超对称生成元理论都更远地偏离了观测结果。

尽管如此，超对称依然在理论家中流行，而且如我们所见，它也是当前弦论的一个关键要素。实际上，优先选择卡丘空间作为描述额外空间维的流形 （见1.10和1.11节），就因为它具有超对称性。这种要求的另一种表述方式是，在 上存在所谓的（非零） 旋量场 ，在整个 上保持不变。名词 旋量场 说的是一种最基本类型的物理场（在A2和A7的意义上）——通常不是固定不变的——可用来描述费米子的波函数。［比较2.5和2.6节；旋量场的更多信息见，［Penrose and Rindler1984］和［1986］的附录（更高维情形）。］

大概说来，这个常旋量场可用来充当超对称生成元的角色，由此可以表示整个高维时空的超对称性质。结果表明，这个超对称性的要求确保时空的全部能量为零。这个零能量态被认为是整个宇宙的基态，这个态因为具有超对称特征而必然是稳定的。这个论证背后的思想似乎是说，零能基态的扰动必然增大其能量，那么被扰动宇宙的时空结构将通过重新释放能量而直接回到那个超对称基态。

然而，我不得不说，我感觉这类论证有很多问题。如1.10节指出的，并考虑本节先前所说的任何超对称几何的体部分可概化为一个经典几何，那么似乎可以恰当地认为那种微扰为我们提供了经典扰动；又因为1.11节的结论，我们必须接受绝大多数的经典扰动可能在远小于1秒的倏忽之间导致时空奇点！（至少，额外空间维的扰动将在弦常数的任何高阶项发生作用之前剧烈增长而产生奇性。）按照这个图景，时空不会平稳回归稳定的超对称基态，而是会挤成一个奇点！即使基态有超对称的性质，我也看不出有什么理由指望它去避免那样的奇点灾难。 LELCwUwCqgAJXkmSw1AAFrwtE6eDmiOHOphtTYiPmnBU7vW7m813dD/Pbh/A+ON+