1.10　函数自由的量子障碍？

本节（及以下）我将提出一个论证，在我看来，它呈现了一个非常有力的例证，说明我们在超维空间的理论中，即使在量子力学背景下，也躲不过超额函数自由度的问题。这个论证基本上就是我在2002年1月举行的霍金60大寿纪念会上的演讲［Penrose 2003］，也见《通向实在之路》31.11和31.12节，但这里的形式更强健。首先，为了理解相关的量子问题（以通常形式呈现的），我们需要从标准的量子理论过程获取更多的东西。

考虑一个简单的量子系统，如一个静止的原子（例如氢原子的系统）。基本上说，我们发现原子存在大量不同的分离的 能级 （如氢原子的电子的不同容许轨道）。系统有一个 最低 能量状态（叫 基态 ），原子的任何其他定态（具有比基态更高的能量）最终都会通过发射光子而衰变到基态——只要原子所处的环境不是“太热”（即能量太高）。（在某些情形，存在一定的选择法则，会禁止某些转化，但这不影响一般的讨论。）反过来说，假如有足够的外来能量（通常以所谓的 光子浴 的电磁能形式，在量子力学语境下也就是 光子 ）并且转移到原子，则原子将从能量较低的态（如基态）提升到能量更高的态。在所有情形下，每个所涉光子的能量 E 都关联一个特殊的频率 ν ，遵从著名的普朗克公式 E = hν （见1.5，1.8，2.2和3.4节）。

现在回看弦论的超维时空问题。弦论家们在窘迫时，似乎普遍表现出一种自满，说那些存在于额外空间维的（巨大的！）函数自由度，不管以什么方式，绝不会跑到我们寻常的空间环境里来。这是因为他们认为那些关乎额外6维空间变形的自由度能成功躲过外来的激发，因为激发那些自由度所需的能量实在太高了。

实际上，额外空间维有些特殊的变形 不用 外来能量也可以激发起来。10维时空就是这样的情形，其中6个额外空间维是卡—丘空间（见1.13和1.14节）。那种变形叫 零模式 ，它们为弦论家提出了一些公认的问题。这些零模式不要求我这里关心的超额函数自由度，我将在1.16节讨论它们。在本节和下节里，我只关心那些确实需要激起全部超额函数自由度的变形，它们需要极高的能量来激发。

为估计所需能量尺度，我们再用普朗克公式 E = hν ，取频率 ν 为信号沿额外维传播时间的倒数量级，这是不会太错的。现在来看，那些小小额外维的尺寸依赖于我们用什么样的弦论。在原始的26维理论中，我们满可以认为其量级为10 -15 m，其所需能量将在LHC的范围内（见1.1节）。而在新的10维超对称弦论中，所需能量要高得多，远远超出了那个地球上最强大的粒子加速器（LHC）或任何其他设想的粒子加速器的能力。在这种类型的弦论（旨在以严格方式解决量子引力问题）中，能量约为普朗克能量（与普朗克长度关联的能量）级，简单的讨论见1.1和1.5节，更详细的讨论见3.6和3.10节。于是，人们通常认为需要某种至少能将单个粒子加速到那么大能量的过程——犹如一颗巨大炮弹爆炸释放能量——才可能从基态激发额外空间维的自由度。至少对额外维那么小的弦论来说，这些维度对眼下可见的任何方式的激发都有着实在的免疫力。

还可以顺带说一下，有些形式的弦论（通常认为在主流之外），其额外维可以认为大如毫米级的尺度。这些理论的所谓优点是它们能经受观测的考验［见Arkani - Hamed et al. 1998］。可是，从函数自由度的观点看，它们遭遇了一个特别的难题：即使用现有的加速器能量，也很容易激发那些“大”震荡能量。我特别感到模糊的是，这些理论的支持者们为什么不担心随之而来的、已然显现的那么大数量的函数自由度。

我还得说（理由在下面说明），我发现，关于额外空间维（即使是普朗克尺度）函数自由度会免于激发的论证，是完全不能令人信服的。因此，我不能太看重额外维自由度在我们目前宇宙能量的“寻常”环境下免受激发的结论。我的怀疑有多个理由。首先，我们要问，为什么要认为普朗克能量在这样的环境下是“大的”呢？我猜测人们倾向的图景就像粒子加速器中的过程，能量从类似高能粒子的主体注入进来（类似于光子将一个原子从基态提升起来）。但我们要记住，弦论家呈现的图景却是，时空——至少当额外维处于其基态时——应视为一个乘积空间 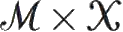（见A7节图A25），其中 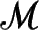多少类似于我们寻常的4维时空经典图像，而 是额外“小”维的空间。在10维形式的弦论中， 通常是卡丘空间，一种特殊的的6维流形（我们将在1.13和1.14节细说）。假如额外维本身会被激发起来，则相关的时空“激发模式”（见A11节）将呈现为我们高维时空的 形式，其中 为扰动（即“激发”）的额外维系统。（当然，在某种意义上，我们要将 视为“量子”而非经典的空间，但这不大影响讨论。）我这里想指出的是，在将 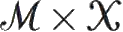扰动成 中，我们是在扰动整个宇宙（ 的每一点所涉及的整个 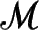空间），因而当我们考虑影响扰动模式所需能量为“大”时，必须在宇宙为整体的背景下来思考。在我看来，要入注的能量量子一定遭受局域高能粒子的影响，是很没道理的。

除此之外，我们还要考虑到某些形式的大概可能是非线性（见A11和2.4节）的不稳定性，会影响（高维）宇宙作为整体的动力学。关于这一点，必须说清楚，我并 不 认为决定6个额外空间维的“内”自由度的动力学 独立于 决定寻常4维时空行为的“外”自由度的动力学。为了名正言顺地将两者都视为一个整体“时空”的组成部分，需要一个在同一纲领下的决定两组自由度的动力学（而不是什么将前者作为后者的“丛”，见A7和1.9节）。实际上，有种形式的爱因斯坦方程就可以认为确定了两组自由度的整体演化，我想那终归也是弦论家心目中的图像，至少在经典水平上是的，其整个10维时空的演化很好地由10维爱因斯坦真空方程 10 G = 0 来逼近（见下面1.11节）。

我将在1.11节讨论这个 经典的 不稳定性问题，现在讨论的关乎量子问题，其结果是，为了严格弄清稳定性问题，我们必须洞彻经典图像。在整体宇宙动力学的背景下，普朗克能量一点儿也不大，而是极其微小。例如，地球绕太阳的运动所涉动能大约比它高亿亿亿（10 24 ）倍！我奇怪的是，这么大的能量，随便一点就远远超过普朗克能量，竟没在地球尺度——或更大的包含整个日地系统——的某个空间区域 里，对空间 有些许扰动。因为在相对大的区域上扩张，那个能量的 密度 在 中会变得极其微小（图1.31）。相应地，这些额外空间维（ ）的几何几乎不会在 上因普朗克尺度的能量扰动而改变，我却没看出丝毫理由，为什么我们自己的局域时空几何 不会被扰动为某个如 的几何——在 之外与 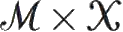的其余部分光滑连接，而 与 的 几何 之间的差别微乎其微，远 小于 普朗克尺度。

主宰整个10维空间的方程会使 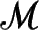的动力学与 的动力学耦合作用，因此 几何的局域的微小变化应是宏观时空几何 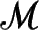的局域（ 邻域）扰动的结果。而且，耦合是相互的。相应地，借助普朗克尺度的自由度源源不断流出的潜在额外维自由度——偶尔也包含大时空曲率——将对宏观动力学产生巨大的效应。

不过，也有来自超对称的论证认为，基态 几何是被高度限制的（如必须限于所谓的6维卡丘空间，见1.13和1.14节），这就不会影响它在动力学状态下发生几何改变的倾向。例如，当爱因斯坦方程 10 G = 0 用于局限于形如 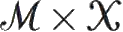空间的几何时，将对 几何本身（以及 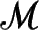的几何）强加限制条件，这种特殊的乘积形式在一般的动力学条件下是不会持续存在的——实际上，几乎所有函数自由度都表达为不具乘积形式的解（见A11节）。于是，不管用什么准则来规定额外维在基态必须具有某样特殊的几何结构（如卡丘空间），我们都不能指望它能在完全的动力学状态下维持。

这里还需要澄清一点，关乎我以前拿原子的量子跃迁来比较，因为我在本节开头讨论静止原子时忽略了一个技术问题。准确地说，原子处于静止，是指它的状态（波函数）必须（技术上说）均匀地在整个宇宙扩展（因为静止，它必须是零动量的，这样才有均匀性；见2.13和4.2节），这有点儿类似 （或 ）在乘积 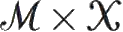的宇宙中均匀扩展。这会不会以什么方式否定我前面的讨论呢？我看不会。这些涉及单个原子的过程总归是局域事件，其中原子态的变化受某些局域过程的影响，例如与其他局域实体（如光子）的相遇。静态（或与时间无关的波函数）原子在技术上应视为整个宇宙的扩展态，这个事实与具体的计算方式无关，因为我们通常只是相对于系统的 质心 来做空间考虑的，没有前面说的困难。

然而，普朗克尺度空间 的扰动，情形就大为不同了，因为 的基态就其本性而言必不会局限于我们寻常时空 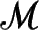的任何特殊位置，而应该无处不在，穿透整个宇宙的时空。 的几何量子态将影响发生在遥远星系的具体物理学过程，正如它影响地球上的过程一样。弦论家认为，相对于实际可能的能量来说，普朗克尺度能量要大得多，而在我看来，激发 在诸多方面都是不合适的。这些能量不仅通过非局域的方式（如地球运动）源源不断地来，假如我们想象 真会通过如此的粒子跃迁（或许归功于某项制造普朗克能量粒子加速器的先进技术）而转换为激发态 ，为新的宇宙态引来空间 ，这显然是荒谬的，正如我们不能指望天鹅座星系的物理学能瞬间为地球上的事件发生改变！我们应该考虑更温和的、以光速向外传播的地球附近的事件。这些事件可以更合理地用非线性经典方程来描述，而不需要陡峻的量子跃迁。

如此考虑来说，我要回到前面提到的问题，看看在 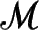的一个相当大的区域 上延展的普朗克尺度的能量量子，会以怎样的方式遂愿地影响该区域上的 空间的几何。如前面指出的， 几乎不怎么受影响，而区域 越大，此区域上的 所需的改变越小，那变化在我们看来就是受普朗克能量的事件扩张的影响。相应地，假如我们想看 在形态或大小上确实发生的巨大变化（它将 变成了截然不同的空间 ），我们就要去考虑远大于普朗克尺度的能量（当然，如此能量在我们熟悉的物理宇宙中是取之不尽的，如地球绕太阳运动的能量）。这些能量不是来自单个“极小”的普朗克尺度能量的量子，而是来自大量源源不断流入 的变化量子。为了在某个大区域上实现从 到大不同的 空间的变换，我们确实需要具备数量庞大的那种量子（如普朗克尺度或更大）。当我们考虑涉及如此多量子的效应时，现在通常是假定那些效应可以纯粹用经典方法（即无须量子力学）来描述。

实际上，我们将在第2章看到，如何能从量子事件的多样性生出经典性来，这个问题确实引出了一串深层的问题，关乎量子世界以何种方式与经典世界发生联系。至于经典性（的出现）是否只是因为涉及了大量的量子或者别的什么准则，倒真是一个有趣（也有争议）的问题，我也要在2.13节来具体讨论。然而，就眼下的讨论来说，问题的微妙也没什么特别的关系，我也只是说，用经典论证来说明时空 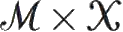的扰动（它确实巨大地改变了空间 ）问题，应该认为是有道理的。我们在下节会看到，这给额外空间维引出了严峻的问题。

但在讨论这些难题——尤其是弦论生出的超空间维的特殊形式——之前，我觉得应该先看一种实验情形，人们有时拿它来类比我们在前面考虑的问题。那种情形的一个例证就是著名的 量子霍尔 （Hall） 效应 ［von Klitzing et al.1980； von Klitzing1983］，那是人们早就确立的一种发生在普通3维空间物理的2维量子现象。在这个现象中存在一个强大的能量壁垒，将相关系统约束在一个2维曲面，而这个低维世界的量子物理，由于没有足以超越壁垒的能量，对额外的第3个空间维来说可以是浑然不觉的。于是，有人指出，我们可以认为这类例子为可能发生在弦论的超维事件提供了类比，我们寻常的3维空间物理，对它所在的9维空间世界来说，也同样是无知无觉的，这是因为存在强大的能量壁垒。

然而，这是一个地道的错误类比。上面的例子其实更适合1.16节的膜世界观，其低维空间是高维空间的 子空间 而非我前面讨论的与标准弦论相关的 因子空间 （如上面的 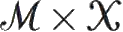表达中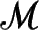， 就是一个因子）。见A7和图1.32。 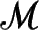作为因子空间（不同于子空间），还与下节的讨论有关。但子空间图像则与截然不同的膜世界图像相关，我们将在1.16节做更完整的描述。 YFavymC4Ti8A4xWqH9YTDZOlLPNpEgwB06bSLXlqMQX6QOA47nk1lkP7Symu9rzi