




我们现在有两个可以选择的5维空间,每一个都为将麦克斯韦电磁学纳入弯曲时空几何提供了一道几何程序。那么,在外尔程序的
S
1
丛表示下(1.8节),5维流形
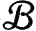 如何与电磁相互作用的5维卡鲁扎—克莱因时空图景(如1.6节)发生联系呢?其实它们是极其相近的,即使把它们看成
完全一样
的也没问题!卡鲁扎的5维时空经克莱因修正后,有着以小圆圈
S
1
为“额外”维度,这与我们用外尔程序构造的丛
如何与电磁相互作用的5维卡鲁扎—克莱因时空图景(如1.6节)发生联系呢?其实它们是极其相近的,即使把它们看成
完全一样
的也没问题!卡鲁扎的5维时空经克莱因修正后,有着以小圆圈
S
1
为“额外”维度,这与我们用外尔程序构造的丛
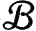 ,在拓扑意义上是一样的。正规说来,它们只不过是普通4维时空
,在拓扑意义上是一样的。正规说来,它们只不过是普通4维时空
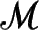 与圆
S
1
的积空间
与圆
S
1
的积空间
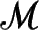 ×
S
1
(见A7图A25和图1.29)。而且,卡鲁扎—克莱因空间自动拥有
S
1
型的丛结构,我们只要找到
闭合的
(且属同一拓扑族的)测地线,就可以视为
S
1
纤维。不过,在各自赋予的结构类型上,外尔与卡鲁扎—克莱因的5维空间还是略有不同。外尔程序要求我们为
×
S
1
(见A7图A25和图1.29)。而且,卡鲁扎—克莱因空间自动拥有
S
1
型的丛结构,我们只要找到
闭合的
(且属同一拓扑族的)测地线,就可以视为
S
1
纤维。不过,在各自赋予的结构类型上,外尔与卡鲁扎—克莱因的5维空间还是略有不同。外尔程序要求我们为
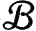 赋予
规范联络
(1.8节),作为4维时空
赋予
规范联络
(1.8节),作为4维时空
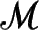 的丛;而在卡鲁扎—克莱因理论中,整个5维流形被视为“时空”,从而
度规
g
被赋予了整个结构。可巧的是,外尔的规范联络恰好已经隐含在卡鲁扎结构中,原来它就取决于1.8节讨论的普通
仿射联络
概念(它对任意黎曼空间成立,因而也适合卡鲁扎的5维空间),只是用于正交于
S
1
纤维的方向而已。于是,卡鲁扎—克莱因5维空间已然包含了外尔的规范联络,可以实际地认为
等同于
外尔的丛
的丛;而在卡鲁扎—克莱因理论中,整个5维流形被视为“时空”,从而
度规
g
被赋予了整个结构。可巧的是,外尔的规范联络恰好已经隐含在卡鲁扎结构中,原来它就取决于1.8节讨论的普通
仿射联络
概念(它对任意黎曼空间成立,因而也适合卡鲁扎的5维空间),只是用于正交于
S
1
纤维的方向而已。于是,卡鲁扎—克莱因5维空间已然包含了外尔的规范联络,可以实际地认为
等同于
外尔的丛
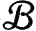 。
。
但卡鲁扎—克莱因空间还真给我们带来了 更多 的东西,因为它的 度规 具有这样的性质:假如它满足适当的爱因斯坦真空场方程 5 G =0(意思是取5维空间的能量张量 5 T 为零),那么我们不仅能得到外尔联络,更惊奇的是还能看到一个事实:从外尔联络涌现出来的麦克斯韦电磁场 F (通过其质量/能量密度)充当着引力场源的角色——方程以这样的形式恰当耦合,被称为 爱因斯坦 — 麦克斯韦方程 。这个惊人事实并不直接来自外尔的方法。
为更精确地说卡鲁扎—克莱因5维空间的结构,我必须指出以上论断其实有一个附带条件:我这里用的是卡鲁扎—克莱因方程的一个特殊形式,它要求赋予 S 1 圈的长度等于贯穿整个5维空间的长度。(理论的有些形式允许长度变化,从而为额外的一个标量场留了余地。)我还要求,那个不变长度的选择应使爱因斯坦场方程(见1.1节)的常数能正确出现为8πγ。最重要的是,在说卡鲁扎—克莱因理论时,我一贯主张用它本来的形式,即在整个5维空间上加一个精确的对称,这样它必然具有 S 1 方向上的完全旋转对称(见基本相似的图1.29)。换句话说,矢量 k 其实是一个基林矢量,从而5维空间可以沿 S 1 线自我滑动,而不至于影响其度规结构。
现在我们说卡鲁扎—克莱因理论中的 函数自由 问题。假如我们用刚才讲的理论形式,那么额外维不会带来更多的函数自由度。因为强化的绕 S 1 曲线的旋转对称,自由度与普通4维时空的情形一样——它具有某个标准形式的从初始3维空间数据得到的确定解——实际上也同爱因斯坦—麦克斯韦方程的情形一样,它在这些情形都是等价的,即等于

对适用于我们宇宙的经典物理理论来说,也应该是这样的。
我想在这儿强调的一点是,这是规范理论——在解释自然力方面取得巨大成功的一类理论——的一个关键特征:丛的纤维
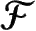 具有适用于规范场的一种(有限维)对称。如A7节严格指出的,正因为我们的
具有适用于规范场的一种(有限维)对称。如A7节严格指出的,正因为我们的
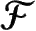 丛具有一种(连续)对称,规范理论才有了用武之地。在电磁相互作用的外尔理论的情形下,那个对称是圆周群U(1)(或等价的SO(2)),它必须精确作用于丛
丛具有一种(连续)对称,规范理论才有了用武之地。在电磁相互作用的外尔理论的情形下,那个对称是圆周群U(1)(或等价的SO(2)),它必须精确作用于丛
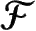 。(符号的意义见A7最后。)在外尔方法中,也正是这个对称整体性地扩张到整个5维流形
。(符号的意义见A7最后。)在外尔方法中,也正是这个对称整体性地扩张到整个5维流形
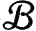 ;它在原始的卡鲁扎—克莱因方法中,也是确定的。为维护高维时空方法(如卡鲁扎引进的)与外尔的规范理论方法之间的密切关系,我们似乎应该根本性地保持纤维对称,将纤维
;它在原始的卡鲁扎—克莱因方法中,也是确定的。为维护高维时空方法(如卡鲁扎引进的)与外尔的规范理论方法之间的密切关系,我们似乎应该根本性地保持纤维对称,将纤维
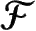 处理为具有内在自由度的时空的恰当组成部分,从而不去实际地(巨大地)增加函数自由度。
处理为具有内在自由度的时空的恰当组成部分,从而不去实际地(巨大地)增加函数自由度。
那么弦论又如何呢?事情好像迥然不同了,因为它隐含着额外空间维应该完全参与动力学的自由度。那样的额外空间维的角色犹如真正的空间维。这是驱动弦论发展的基本哲学的重要组成部分,因为它认为,弦在那些额外维中所能容许的“振动”应该解释所有的力和所需的参数,从而为粒子物理学的所有特征提供包容的空间。从我的观点看,这是非常错误的哲学——让额外空间维自由卷入动力学,给我们打开了真正的恶自由度的潘多拉盒子,再想关上它就希望渺茫了。
不过呢,弦论的支持者们并不在乎这类困难(这是额外空间维的多余函数自由度自由生成的),他们选择了不同于卡鲁扎—克莱因纲领的过程。他们的部分努力是解决弦量子论的参数不变性要求所产生的反常。1970年以来,他们就被赶着(为玻色弦)用一个全动力学的26维时空,其中25个是空间维,剩下一个是时间维。接着,在格林(Michael Green)和许瓦兹(John Schwarz)1984年的理论进展的影响下,弦论家们设法借助超对称性(见1.14节,但1.6节已经提到过)将空间维减少到9(费米弦),但这样的空间维缩减对我要提出的问题没什么影响(因为它并没将空间维减少到我们直接感受的3)。
在我努力去认识弦论各家进展的过程中,还遇到一点潜在的困惑,特别是在理解函数自由度问题的时候。问题在于,关于究竟什么是时空维度,我们的观点常常游移不定。我想其他众多旁观者在费力去理解弦论的数学结构时,肯定也有同样的疑惑。我们有着某个特定维数的环境时空的思想,在弦论中的角色似乎不如在传统物理学中那么重要,当然也不是我满意的那类角色。尤其困难的是评估一个物理学所包含的函数自由度,除非我们对它真实的时空维度有一个明确的概念。
为更明确这个问题,我还是回到初始弦论特别诱人的一面(如1.6节概括的)。就是说,弦的经历可以看成 黎曼曲面 ,即复曲线(见A10),从数学观点看,这是特别精美的结构。有时我们就用名词“世界片”来说这种弦的历史(类似于传统相对论中粒子的世界线的概念;见1.7节)。在弦论之初,人们有时是从2维 共形场论 的观点来看弦[Francesco et al.1997; Kaku 2000; Polchinski 1994,第一章;2001,第二章],这样,大致说来,弦论时空就完全类似于一个2维世界片!(回想1.7节讲的时空背景下的共形概念。)这就给我们呈现这样一幅图景,它的函数自由度有如下形式( a 为一定的正数):

我们如何将它与普通物理学要求的更大的函数自由度
 协调呢?
协调呢?
答案似乎在于,世界片通过某种幂级数的展开多少“嗅出”了周围的时空和附近的物理,其中所需的信息(有效的幂级数系数)会通过无限多个参数(其实是世界片上的全纯量,见A10)呈现出来。表面看来,那无限多个参数犹如在以上的表达式中让“ a =∞”,但这不起什么作用(因为A11末尾提出的理由)。我想在这儿指出的,当然不是说函数自由度可能在某种意义上不相干或被错误定义。相反,我要说的是,对依赖于幂级数的系数或模式分析的某种方式建立的理论来说,完全不容易确定函数自由度是什么(A11)。不幸的是,这种形式似乎常常就是人们对弦论的各种方法所采纳的东西。
一定程度上,弦论家中间好像流行一种观点,认为清楚地认识什么是时空维度,是至关重要的。在一定意义上,维度可以假定为一种能量效应,那么随能量的增大,系统有可能接近更多的空间维。于是可以认为,存在隐藏的维度,能量越高,显露的维度越多。这幅图景的模糊不清令我有些许困惑,特别是关于理论内在的函数自由度问题方面。
有个例子出现在所谓的“杂化”弦论。理论有两个形式,分别叫HO 理论 和HE 理论 。两者的区别对我们现在无关紧要,但我等会儿还是想说几句。杂化弦论的奇异特征是,它似乎同时活动在26个时空维和10个时空维(后者伴随超对称),就看我们关心的是弦的左行激发态还是右行激发态——这种(依赖于弦的必须赋予的方向的)区别也需要解释,我过会儿再说。假如我们想知道其中的函数自由度(就眼下说,把每个纲领都当经典理论处理),那么维度的矛盾将给我们带来很多问题。
对这个显然的困境,官方的解决办法是认为两种情形的时空都是10维的(1维时间和9维空间),但还有额外的16个空间维,在两种情形下不得不以不同的方式来处理。就左行激发态说,所有26维一起考虑,作为弦可以在其中扭摆的时空。然而,对右行激发态来说,26维中的不同方向要以不同方式来解释。其中10个是弦扭摆的方向,其余16个则被认为是纤维的方向。所以,就弦来说,这幅图景在右手振动模式下就是一个10维基空间加16维纤维的纤维丛(A7)。
与一般的纤维丛情形一样,一定有伴随纤维的
对称群
,对HO理论来说就是SO(32)(32维空间里球面的非反射旋转,见A7),对HE理论来说就是群
E
8×
E
8,这里
E
8是一类有着特殊数学意义的对称群,叫
例外简单连续群
。当然了,这种例外单群——
E
8是其中最大也最迷人的——特别的内在的数学意义,激励着一帮人走上了美学的方向(见1.1节)。然而,从函数自由度的观点看,重要的问题是,不论在纤维丛描述中用哪个群,自由度都有
 的形式,适用于弦振动的费米(右行)模式;而要适合玻色(左行)模式,自由度的形式应该是
的形式,适用于弦振动的费米(右行)模式;而要适合玻色(左行)模式,自由度的形式应该是
 。这与我们以前遇到的一个问题有密切的联系:我们曾考虑过原始的卡鲁扎—克莱因理论(或外尔的圆丛理论,见1.8节)的函数自由度(形如
。这与我们以前遇到的一个问题有密切的联系:我们曾考虑过原始的卡鲁扎—克莱因理论(或外尔的圆丛理论,见1.8节)的函数自由度(形如
 )与完全5维时空理论的函数自由度(形如
)与完全5维时空理论的函数自由度(形如
 )之间的差别。这里,必须明确区分丛(具
r
维纤维
)之间的差别。这里,必须明确区分丛(具
r
维纤维
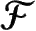 )的总空间的维度
d
+
r
与
d
维基空间
)的总空间的维度
d
+
r
与
d
维基空间
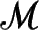 的维度。详细描述见A7。
的维度。详细描述见A7。
以上问题关乎时空整体所具有的函数自由度,与其中出现什么样的弦世界片毫不相干。不过,我们这里真正感兴趣的是在那个时空中的弦世界片具有的自由度(见1.6节)。对某些位移模式(如费米模式)来说,时空呈现为10维,而对另外的模式(如玻色模式)它却是26维。怎么会这样呢?对玻色模式,图像一目了然。弦可以在时空里扭摆,函数自由度为
 (“1”的来源是,即使弦世界片是2维曲面,我们也只考虑右行激发态的1维空间)。但是当我们考虑费米模式时,我们要把弦看成是栖息在10维“时空”里,而不是“坐在”它的26维纤维丛上。就是说,弦必须把丛的那些纤维戴在自己身上。这是与玻色模式截然不同的实体,弦自己成了它栖息的26维时空丛的总空间里的18维子丛。(这个事实没得到正式认可。有效时空是26维丛的10维因子空间——见1.10节图1.32和A7,所以弦世界片也必须是因子空间,这时是18维子丛的因子空间。)在这些模式中,函数自由度仍然是
(“1”的来源是,即使弦世界片是2维曲面,我们也只考虑右行激发态的1维空间)。但是当我们考虑费米模式时,我们要把弦看成是栖息在10维“时空”里,而不是“坐在”它的26维纤维丛上。就是说,弦必须把丛的那些纤维戴在自己身上。这是与玻色模式截然不同的实体,弦自己成了它栖息的26维时空丛的总空间里的18维子丛。(这个事实没得到正式认可。有效时空是26维丛的10维因子空间——见1.10节图1.32和A7,所以弦世界片也必须是因子空间,这时是18维子丛的因子空间。)在这些模式中,函数自由度仍然是
 (这里
a
依赖于丛的群),但现在的几何图像完全不同于玻色模式了。玻色模式的弦要看成是2维的世界管(如图1.11),但费米模式的弦从技术上看应该是总维度为18(=2+16)的子丛!我发现很难为它的活动构想一幅和谐的图景,我也没见过有谁恰当讨论过这些几何问题。
(这里
a
依赖于丛的群),但现在的几何图像完全不同于玻色模式了。玻色模式的弦要看成是2维的世界管(如图1.11),但费米模式的弦从技术上看应该是总维度为18(=2+16)的子丛!我发现很难为它的活动构想一幅和谐的图景,我也没见过有谁恰当讨论过这些几何问题。
除了考虑周围时空以外,我这里还应该把左行和右行模式的几何性质说得更明确些,因为这引出了另一个我还没说的问题。我提到过弦世界片可以看作 黎曼曲面 的诱人事实。然而以上的描述却不是这样的。我用了量子(场)论的一个很普通的技巧(这里也还在用着),借助一种叫 维克旋转 的方法,只是一直没明确指出而已。
维克旋转是什么呢?是一个数学过程,起初是为了将闵可夫斯基时空
 (即狭义相对论的平直时空,见1.7节末)中的不同量子场论问题转换为常常更好处理的普通欧几里得4维空间
(即狭义相对论的平直时空,见1.7节末)中的不同量子场论问题转换为常常更好处理的普通欧几里得4维空间
 中的问题。这想法源自如下的事实:如果标准的时间坐标
t
代以i
t
(
中的问题。这想法源自如下的事实:如果标准的时间坐标
t
代以i
t
(
 ,见附录A9),则相对论的洛伦兹时空度规
g
就转换为欧几里得空间中的(负)度规。这个技巧有时也叫欧几里得化,通过一种
解析延拓
过程(见附录A10和3.8节),它又可以转换回去,成为闵氏时空
,见附录A9),则相对论的洛伦兹时空度规
g
就转换为欧几里得空间中的(负)度规。这个技巧有时也叫欧几里得化,通过一种
解析延拓
过程(见附录A10和3.8节),它又可以转换回去,成为闵氏时空
 的一个解。维克旋转思想如今在量子场论中太普通了,在五花八门的情形中几乎成为不言而喻的自动过程,而其有效性从未遭遇质疑。诚然,它用途广泛,但也绝非万能。最特别的是,它在广义相对论的弯曲时空背景下疑点重重,几乎不能用于通常的情形,因为不存在
自然的时间坐标
。在弦论中,这既是10维时空中的问题,也是一般弯曲时空和弦世界片上的问题
的一个解。维克旋转思想如今在量子场论中太普通了,在五花八门的情形中几乎成为不言而喻的自动过程,而其有效性从未遭遇质疑。诚然,它用途广泛,但也绝非万能。最特别的是,它在广义相对论的弯曲时空背景下疑点重重,几乎不能用于通常的情形,因为不存在
自然的时间坐标
。在弦论中,这既是10维时空中的问题,也是一般弯曲时空和弦世界片上的问题
 。
。
在我看来,这类困境引发的问题尚未真正在弦论中得到充分解决。不过,我们暂且忽略一般的问题,来看看弦世界片的欧化效应会带来什么结果。我们可以将弦的历史形象化为以某种方式运动的一个圈(不超过局地的光速)。那么它的世界片是一个类时2维曲面,从周围时空的10维洛伦兹度规继承下一个2维洛伦兹度规。2维度规为世界片的每一点赋予一对零方向。我们紧贴着这个或那个零方向绕一圈,会得到世界片柱面上的右旋或左旋的螺旋零曲线。沿这两族曲线不变的激发态将生成前面所说的右行或左行模式(图1.30b)。然而,这样的柱形世界片不会分叉形成我们需要的如图1.11所示的图景,因为洛伦兹结构在管道分叉处会出问题。这种拓扑只能出现在图1.30a的欧化弦,它们是黎曼曲面,具有黎曼型度规,没有零方向,可以解释为 复曲线 (见附录A10)。现在,欧化的右行或左行模式分别对应于黎曼曲面上的 全纯 或 反全纯函数 (附录A10)。

本节关注的 函数自由 问题,在我读过的标准文献中,似乎没有在弦论考虑中得到严肃的阐释。这样有直接物理意义的问题,在弦论中也不是唯一的。实际上,我也没看出它与前面提到的基本却高度可疑的维克旋转过程所引发的几何问题有多大关系。我感觉,从弦论观点生出的许多明显的几何和物理问题,从来就没有恰当地讨论过!
例如,在杂化弦论的情形,弦一定是闭合的,意味着它们没有洞。(见1.6节,特别是1.16节。)如果想以直接的物理方式考虑这些弦——就是说,在玩儿维克旋转的“特技”之前——则我们必须认为弦的世界片是类时的(如图1.30b)。假如世界片是无孔洞的,则它必然继续是向未来无限延伸的类时管。认为它缠绕着“微小的”额外维是毫无意义的,因为那些维度都是类空的。它只能向未来无限延展,而并不真是闭合的。这也是我所见的任何弦论描述都没有恰当解决的众多问题之一。
如何从普通的物理学概念来看弦论呢?竟然没有一幅和谐的几何图像,我看这是非常怪异的事情,更何况那理论还常常被奉为什么 万物之理 。而且,与这些考虑中几何和物理图像缺失形成鲜明对比的是,弦论有着高度精巧的几何与6维流形的极其精细的纯数学分析——通常即卡拉比—丘空间,见1.13和1.14节,人们认为它们生成了弦论的和谐所需要的普朗克尺度的额外6个卷曲空间维。如此的一幅图景,一方面是几何的大杂糅,另一方面却似乎无视总体的几何一致性,但为物理学群体的大部分所接受,这在我看来也是极端困惑的!
在下面两节的函数自由度讨论中,我将在10维时空下说话,但论证并不针对特定的维数。1.11节关于额外维极不稳定的经典论述,也适用于至少具有2个额外(微小)空间维并满足10维爱因斯坦( Λ =0)真空方程 10 G = 0 (时间维保持为1)的任何超维理论。在标准文献中也有论证指出,原始的26维玻色弦论其实也是极不稳定的,但那与我这里的论证(适用面更广)没什么特别关系。
1.10节的论证与1.9节有着截然不同的特征,它针对的是人们常说的一个量子力学论证:微小的额外空间维不会受未来任何可能尺度的能量的激发。这个论证仍然不限于特定的额外空间维数,但为明确起见,我也用时下流行的10维理论的语言来说话。不论哪种情形,我都不关心超对称性,于是这些几何概念仍然是图像清晰的。我假定超对称的存在不会剧烈影响论证,因为所给的这些论证可以阐明几何的非超对称“体”(见1.14节)。
在所有这些论证中,我都采纳了似乎是弦论所要求的观点,即额外空间维是完全动态的。于是,尽管弦论家们常说弦论的额外维与卡鲁扎和克莱因引入的额外维存在某些相似,我还是要强调原始的卡鲁扎—克莱因纲领与弦论家们所想的有着根本的差别。在我所见的所有形式的高维弦论中(或许除了与本节开头描述的杂化模式的16个不和谐维度有关的理论),其实并不存在任何类似于卡鲁扎—克莱因理论所采用的额外维中的旋转对称的东西——实际上,这种对称被隐性地否决了[Greene1999]。相应地,对现在约定的10维理论来说,弦论的函数自由度可能是过分超额了,大约为
 而不是我们为现实的物理理论所预期的
而不是我们为现实的物理理论所预期的
 。关键的一点在于,在卡鲁扎—克莱因理论中,我们不能自由地沿着额外空间维(
S
1
)任意改变结构(因为受旋转对称的约束),而在弦论中,那个自由度是明确容许的。正是这一点决定着弦论会出现过量的函数自由度。
。关键的一点在于,在卡鲁扎—克莱因理论中,我们不能自由地沿着额外空间维(
S
1
)任意改变结构(因为受旋转对称的约束),而在弦论中,那个自由度是明确容许的。正是这一点决定着弦论会出现过量的函数自由度。
这个问题,就经典(即非量子)考虑来说,我从没见有哪个专业的弦论家说清楚过。另一方面,则有人指出那些考虑与弦论无关,因为它们只能从量子力学(或量子场论)而不是经典场论的观点来说明。实际上,当额外6维“小”空间的过量自由度问题出现在弦论家们面前时,常常被一般性的量子力学论证(在我看来基本是错的)轻描淡写地消去。我将在下一节讨论这种论证,然后(在1.11节)我自己举一个例子,那论证并非全然不可信,但弦论家额外空间维的逻辑结果却是完全不稳定的宇宙,其中的额外维将发生动力学坍缩,导致我们熟悉的宏观时空几何的灾难后果。
这些论证主要牵涉时空几何本身的自由度,在高维时空流形定义的其他领域也有一个独立但密切相关的关于过量函数自由度的问题。我将在1.10节的末尾简短地讨论这些问题,偶然也提出与实验状态的一定关联。我将在2.11节略谈一个相关的问题,尽管还有多少不确定的东西,但也涉及一些堪忧的问题,我也没见别人谈过,值得进一步研究。