




外尔1918年提出一个新想法,把电磁场融入广义相对论,将时空的度规结构弱化为前面描述的一种共形结构,这样就没有了绝对的时间流的度量,不过还有度规定义的零锥[Weyl1918]。此外,外尔的理论中还有“理想时钟”的概念,这样我们就能参照某个 特殊的 时钟,为类时曲线定义一个“长度”,尽管度量的时间流依赖于那个时钟。但是,在外尔的理论中,不存在绝对的时间标度,因为没有哪个时钟有特别优越的地位。而且,我们可以有两个这样的以完全相同的节律嘀嗒的时钟,它们在同一个事件P相对静止,但如果沿不同时空路径到达另一个事件Q,我们会发现两个钟在到达时的节律是不一样的,即在Q点 相对静止 的两个时钟这时不再以相同节律嘀嗒了。见图1.26a。重要的是要注意,这个情形不同于爱因斯坦相对论的双生子详谬,它更加极端。在那个详谬的情形中,时钟读数可能依赖于时钟的历史,而时钟的节律却不会。外尔更一般的几何在时钟节律中引出一个奇异的时空“曲率”,它度量了无穷小尺度上的时钟节律偏移(图1.26b)。正如我们在图1.27看到的,这类似于曲面曲率度量角度的偏离。外尔证明了描述他那个曲率的量 F 与麦克斯韦理论中描述自由电磁场的量恰好满足同样的方程!于是外尔提出, F 在物理上等同于麦克斯韦的电磁场。
只要有了在事件P的零锥概念,时间和空间的度量在P的任何邻域中就基本上是相互等价的,因为零锥确定了P的光速。用普通的话说就是,光速使空间和时间能相互转换。例如,一年的时间间隔相当于一光年的距离,而一秒相当于一光秒,等等。实际上,在现代测量中,时间间隔比空间间隔的直接测量要精确得多,所以现在我们将米 精确 定义为1/299792458光秒(则光速现在等于一个精确的整数:每秒299792458米)!这样看来,著名相对论专家辛格[J. L. Synge1921,1956]为时空结构提出的名词“测时学”(而不是“几何学”)是非常确切的。
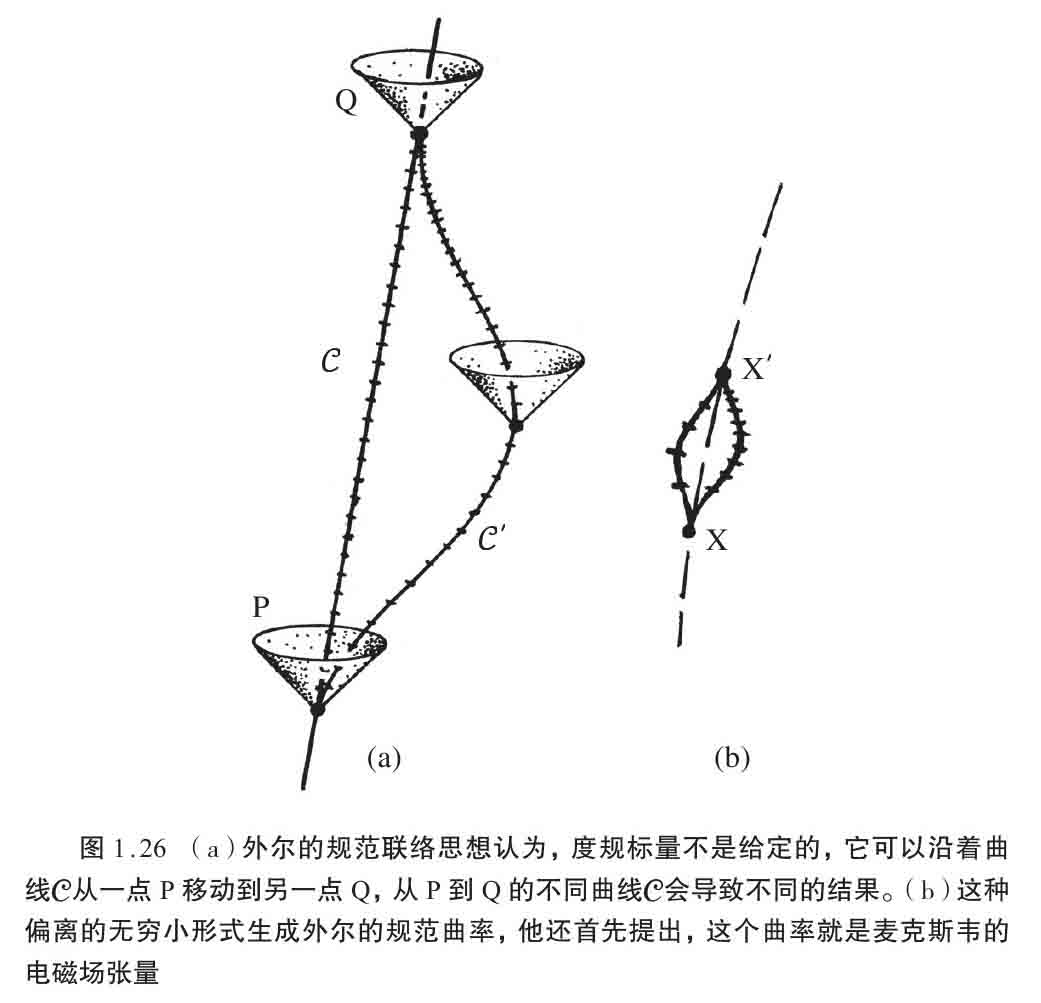
我用时间测量描述了外尔的思想,但外尔想的可能是空间位移,他的纲领被称为
规范理论
,“规范”指的就是用以度量物理距离的标度。外尔思想的一个亮点在于,规范不需要为整个时空一劳永逸地整体确定。假如在事件P确定一个规范,并给定连接P到另一个事件Q的曲线
 ,则规范可以唯一地沿曲线从P迁移到Q。但如果还有连接P与Q的另一曲线
,则规范可以唯一地沿曲线从P迁移到Q。但如果还有连接P与Q的另一曲线
 ,则沿
,则沿
 迁移到Q会产生不同的结果。定义这个“规范迁移”过程的数学量叫
规范联络
,而不同迁移路径产生的结果的偏离则是
规范曲率
的度量。应该指出,外尔能产生规范联络的精彩想法,大概是因为他熟悉任意(伪)黎曼流形自动拥有的另一种联络——
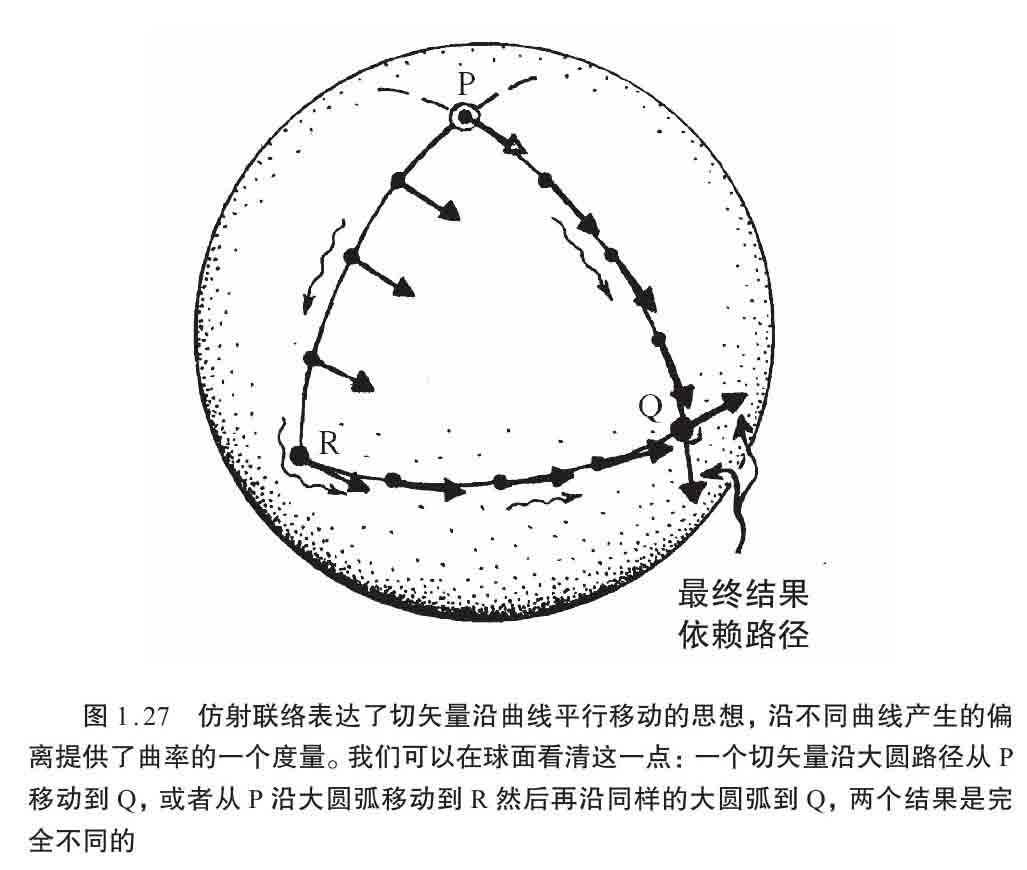
仿射联络
——它与切矢量沿曲线的平行移动有关,也与路径有关,图1.27的球面例子很好地说明了这一点。
迁移到Q会产生不同的结果。定义这个“规范迁移”过程的数学量叫
规范联络
,而不同迁移路径产生的结果的偏离则是
规范曲率
的度量。应该指出,外尔能产生规范联络的精彩想法,大概是因为他熟悉任意(伪)黎曼流形自动拥有的另一种联络——
仿射联络
——它与切矢量沿曲线的平行移动有关,也与路径有关,图1.27的球面例子很好地说明了这一点。
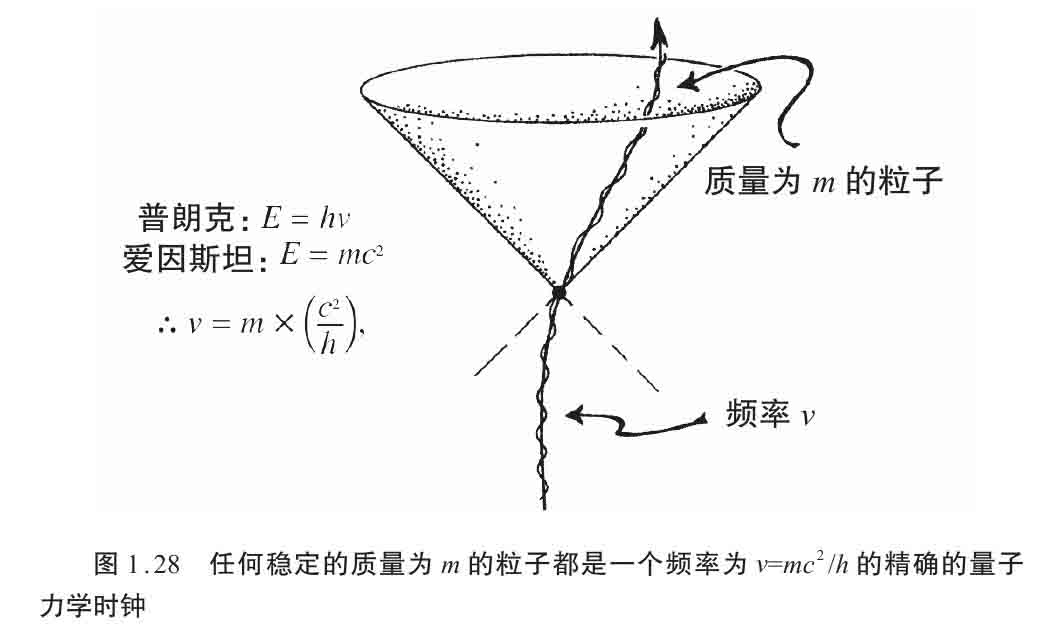
爱因斯坦听说外尔的天才想法时,很感兴趣,但他指出,从物理的观点看,那个纲领有严重缺陷,根本在于物理的原因,即粒子质量提供了确定的沿它的世界线的时间度量。这一点可以通过普朗克(Max Planck)的量子关系
E = hν
与爱因斯坦自己的
E = mc 2
来说明(图1.28)。这里, E 为粒子能量(在它自己的坐标系中), m 是它的(静止)质量, ν 是粒子根据基本量子力学(见2.2节)获得的频率(即粒子的“嘀嗒”节奏), h , c 分别为普朗克常量和光速。于是,结合 hν (= E ) = mc 2 ,我们看到单个粒子总有一个精确的频率正比于它的质量:
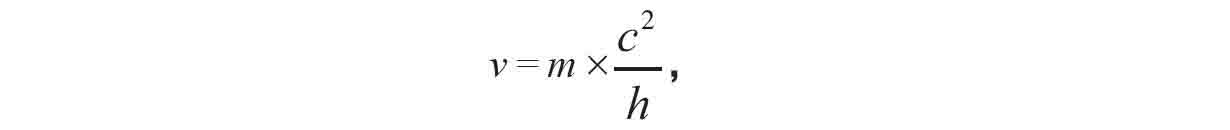
量 c 2 / h 是一个普适常数。于是,任何稳定粒子确定了一个由这个频率给定的非常精确的时钟节律。
然而,在外尔的建议中,任何这样的时钟节律都必然 不 是一个固定的量,而是依赖于粒子的历史。相应地,粒子质量也将依赖于它的历史。特别是,在我们上面的情形中,假如我们认为两个电子在事件P中是相同的粒子(这其实是量子力学要求的),那么,当他们经由不同路线到达事件Q时,它们将具有不同的质量,也就是它们到达Q后就不可能是相同的粒子了!这实际上根本性地背离了量子论确立的原理——原理要求用在全同粒子的法则迥然有别于用在非全同粒子的法则(见1.14节)。
看来,外尔的想法颠覆了某些基本的量子力学原理。不过峰回路转,也正是量子论,在1930年前后完全确立之后(主要靠狄拉克和冯诺依曼,还有外尔本人[Dirac 1930; von Neumann 1932; Weyl 1927]),挽救了外尔的思想。我们将在第2章看到(2.5和2.6节)粒子的量子描述用的是
复数
(见A9)。我们已经在1.4节看到,复数扮演的基本角色是量子力学叠加原理中的系数(量
w
和
z
)。我们以后还将看到(2.5节),若所有系数乘以同一个
单位模
的复数
u
(即
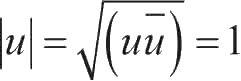 ,从而
u
在维塞尔面的单位圆上,见附录A10),则物理状态保持不变。我们注意到,棣莫弗—欧拉(Cotes De Moivre—Euler)公式(见A10)表明,这样的
幺模
复数
u
可以写成
,从而
u
在维塞尔面的单位圆上,见附录A10),则物理状态保持不变。我们注意到,棣莫弗—欧拉(Cotes De Moivre—Euler)公式(见A10)表明,这样的
幺模
复数
u
可以写成
u = e iθ = cos θ +isin θ ,
其中 θ 为从原点到 u 的直线与 x 正方向的夹角(以逆时针弧度为度量)(见A10图A13)。
在量子力学背景下,幺模复因子常被称为 相 (或相角),在量子论的形式中是一种不能直接观察的东西(见2.5节)。外尔独创却怪异的思想之所以成为现代物理学的关键要素,是因为一点微妙的改变,就是将外尔的正实数标度因子——即 规范 ——代以量子力学的 复相 因子。由于这些历史的原因, 规范 一词就定下来了,尽管以那种方式修正的外尔理论也许更适合叫 相 理论,而 规范联络 也该叫 相联络 。不过,假如现在真把名词照这样改了,可能会令更多的人感到混乱而非帮助。
更准确地说,外尔理论中出现的相与量子形式的(一般性的)相并不完全一样,两者之间差一个粒子
电荷
给定的因子。外尔理论的根本特征在于存在一种所谓的
连续对称群
(见A7最后一段),它作用于时空的任何事件P。在外尔原来的理论中,对称群由所有正实数因子组成,从而可以放大或缩小规范。这些可能的因子就是不同的
正实数
,其空间即数学家所说的空间
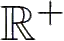 ,所以这里的对称群有时也叫乘法群
,所以这里的对称群有时也叫乘法群
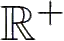 。在后来更有物理意义的外尔电磁理论形式中,群元素是维塞尔平面的旋转(无反射),叫SO(2)或U(1),群元素用单位模复数e
iθ
表示,这些元素提供了维塞尔平面中单位圆的不同旋转角度,这里,我把单位半径的圆周简单记为
S
1
。
。在后来更有物理意义的外尔电磁理论形式中,群元素是维塞尔平面的旋转(无反射),叫SO(2)或U(1),群元素用单位模复数e
iθ
表示,这些元素提供了维塞尔平面中单位圆的不同旋转角度,这里,我把单位半径的圆周简单记为
S
1
。
应该指出(关于这里的记号,以及群的记号,见A7末段),SO(2)的“O”代表“正交”,意思是,我们关心旋转群(即保持正交(直角),在这里是2维旋转,即SO(2)里的“2”)。“S”代表“特殊”,指的是这里排除了反射。至于“U(1)”,“U”代表“单位的”(保持复向量的单位模性质),指复数空间中的一种旋转,我们将在2.5~2.8节讨论。不管什么记号,我们关心的就是普通圆周 S 1 的旋转(不管反射)。
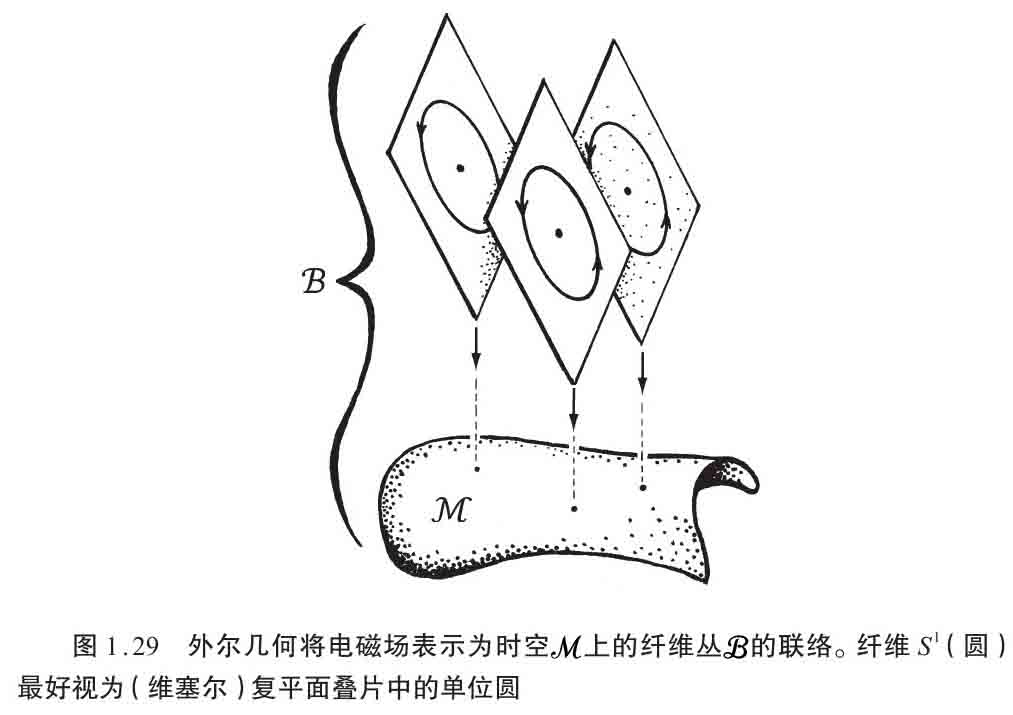
现在我们看到,外尔联络并非真的用于时空流形
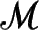 的概念,因为圆
S
1
并非真是时空的一部分。
S
1
其实是与量子力学有确定关系的一个抽象的空间。不过,我们还是可以认为
S
1
扮演着一个几何角色,即基空间为时空流形
的概念,因为圆
S
1
并非真是时空的一部分。
S
1
其实是与量子力学有确定关系的一个抽象的空间。不过,我们还是可以认为
S
1
扮演着一个几何角色,即基空间为时空流形
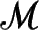 的丛
的丛
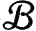 的纤维。这个几何如图1.29。纤维是圆
S
1
,但我们在图中看到,最好将这些圆视为(维塞尔)复平面“叠片”(见A10)中的单位圆。(纤维丛的记号,读者参看A7。)外尔的规范联络其实是几何的概念,而不会为时空赋予纯粹和简单的结构;它提供的结构赋予了丛
的纤维。这个几何如图1.29。纤维是圆
S
1
,但我们在图中看到,最好将这些圆视为(维塞尔)复平面“叠片”(见A10)中的单位圆。(纤维丛的记号,读者参看A7。)外尔的规范联络其实是几何的概念,而不会为时空赋予纯粹和简单的结构;它提供的结构赋予了丛
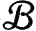 ,是一个与4维时空流形密切相关的5维流形。
,是一个与4维时空流形密切相关的5维流形。
外尔思想还通过规范联络推广到了粒子物理学标准模型的强弱相互作用(1.3节),同样可以用A7的纤维丛描述。在每种情形,基空间都和前面一样是4维时空,但纤维是比我们用来描述电磁场的1维
S
1
更高维的空间
 。外尔的规范方法向麦克斯韦理论的推广,叫杨(振宁)—米尔斯(Mills)理论[Chan and Tsou 1998]。在强相互作用的情形下,空间
。外尔的规范方法向麦克斯韦理论的推广,叫杨(振宁)—米尔斯(Mills)理论[Chan and Tsou 1998]。在强相互作用的情形下,空间
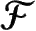 与夸克的可能色荷的空间有着相同的对称性,与1.3节的描述一致。这里的对称群叫SU(3)。弱相互作用的情形在表面上是相似的,其群为我们熟悉的SU(2)(或U(2)),但因为在宇宙膨胀早期发生了对称破缺的过程,弱相互作用的对称被认为是破缺的,这一点给理论留下一定的模糊。实际上,我发现在这些过程的通常描述中存在一些多少令人忧虑的问题,因为严格说来规范对称的思想并非真的有效,除非对称确实是精确的(见A7和《通向实在之路》28.3节)。幸运的是,在我看来,通常那种过程是可以重构的,其中弱力通过某种多少不同于标准模型的物理解释的机制发生作用,大致说来就是假定轻子具有类色夸克的组成(类似于强子的夸克组成),而其中的弱相互作用对称总是精确的['t Hooft1980b; Chan and Tsou1980]。
与夸克的可能色荷的空间有着相同的对称性,与1.3节的描述一致。这里的对称群叫SU(3)。弱相互作用的情形在表面上是相似的,其群为我们熟悉的SU(2)(或U(2)),但因为在宇宙膨胀早期发生了对称破缺的过程,弱相互作用的对称被认为是破缺的,这一点给理论留下一定的模糊。实际上,我发现在这些过程的通常描述中存在一些多少令人忧虑的问题,因为严格说来规范对称的思想并非真的有效,除非对称确实是精确的(见A7和《通向实在之路》28.3节)。幸运的是,在我看来,通常那种过程是可以重构的,其中弱力通过某种多少不同于标准模型的物理解释的机制发生作用,大致说来就是假定轻子具有类色夸克的组成(类似于强子的夸克组成),而其中的弱相互作用对称总是精确的['t Hooft1980b; Chan and Tsou1980]。