




我们更具体地来看看那种发散是怎么出现的。在粒子物理学中,我们需要考虑的是几个粒子共同产生其他粒子的情形,其中有的粒子会分裂成其他粒子,而有的粒子对会重新结合形成其他粒子,而这些粒子也同样会卷入这个复杂的生灭过程。粒子物理学家经常遇到的情形是一个特定的粒子集合——粒子间常有近光速的相对速度——这些粒子的碰撞和分裂的组合产生某个新的粒子集合。整个过程涉及与给定初始和生成粒子集合相应的所有可能类型的中间过程的大量量子叠加。如图1.3的 费曼图 就显示了这样的一个复杂过程。
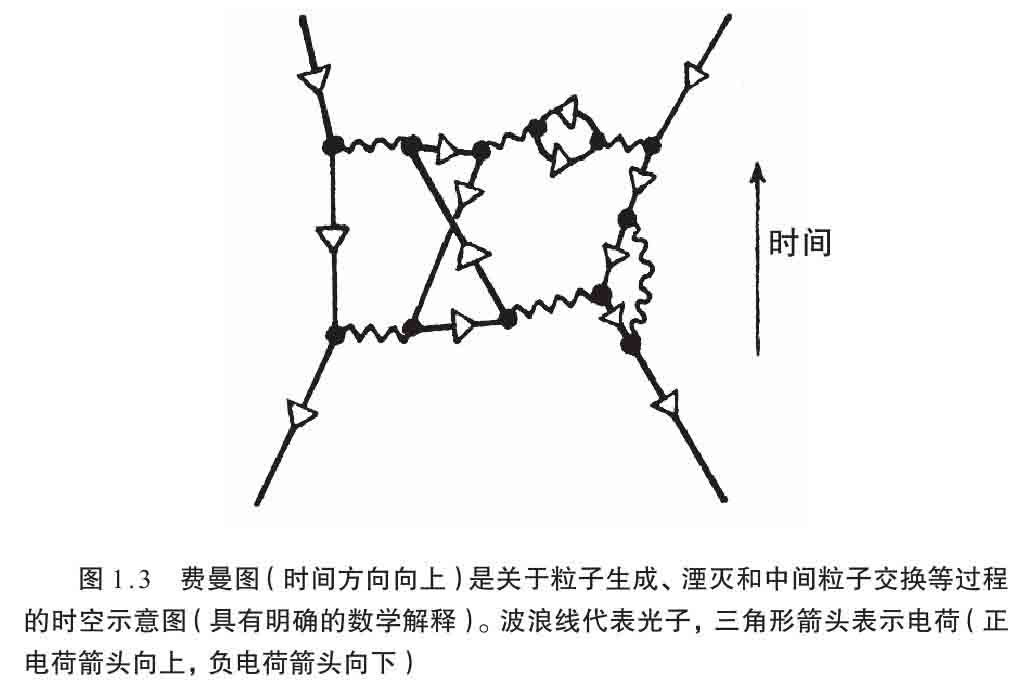
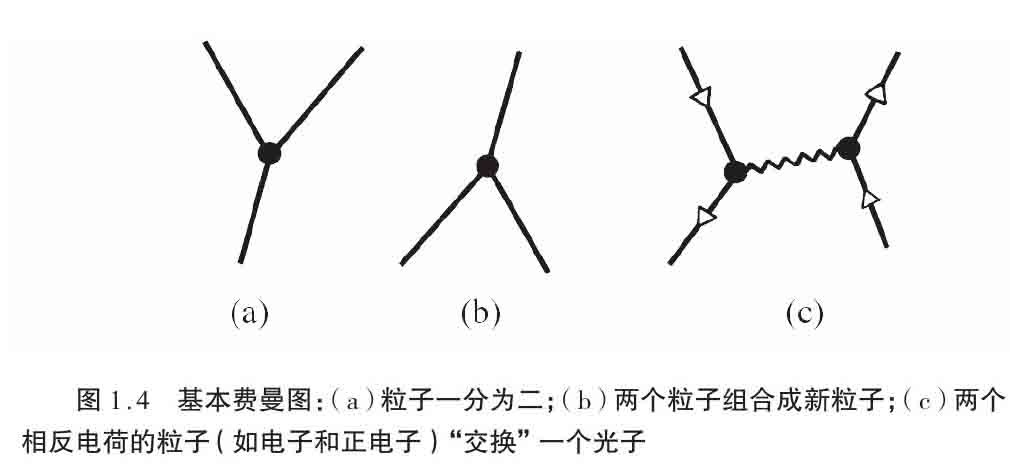
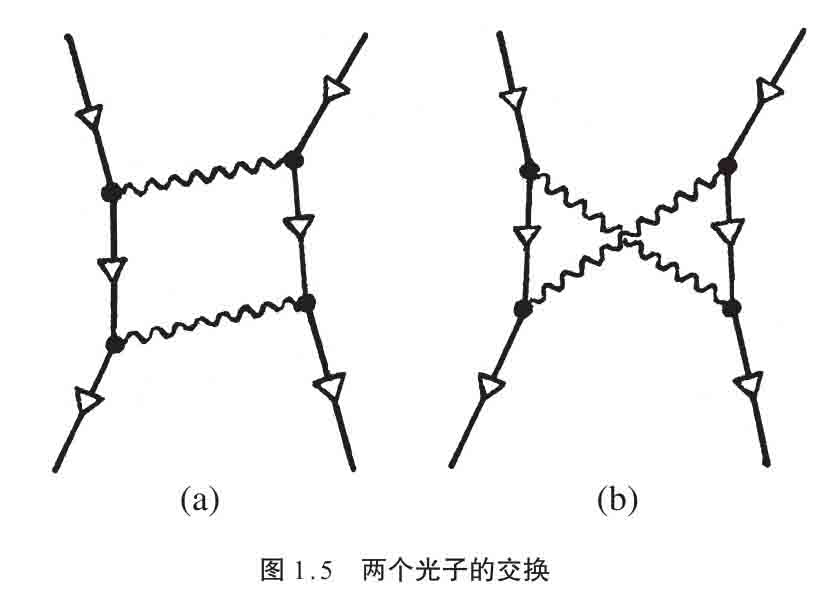
将费曼图看成特定所涉粒子过程集合的时空图,也不算太离谱。我是研究相对论的,不是粒子物理学或QFT专家,喜欢用沿页面向上来表示时间,而专家们通常用从左向右来表示时间方向。费曼图以美国物理学家费曼(Richard Phillips Feynman)的名字命名。图1.4列举了几个基本图样。其中,图1.4a表示一个粒子分裂成两个粒子,1.4b表示两个粒子结合形成第三个粒子。在图1.4c中我们看到在两个粒子之间交换一个粒子(如光子,即电磁场或光的量子,以波浪线表示)。在这个过程中用“交换”一词,虽然是粒子物理学家的惯用法,还是显得有点儿奇怪,因为 单个 光子只是从一个端点的粒子传到另一个——尽管分不清哪个粒子发射,哪个粒子吸收。这种交换的光子通常被称为 虚 粒子,它的速度不受相对论要求的约束。口头说的 交换 也许更适合图1.5b所示的过程,尽管图1.5的过程一般说来是两个光子的交换。
可以认为一般的费曼图是由多个这样的基本图以所有可能的组合方式组成的。然而,叠加原理告诉我们,不要考虑这种 单 费曼图表示的粒子碰撞过程是如何发生的,因为有很多可能性,而实际的物理过程是由众多不同费曼图的某个复杂的线性组合表示的。每个图对总叠加的贡献量——本质上即我们在1.4节遇到的 w 或 z 那样的复数——才是我们需要从任何特定费曼图计算的东西,这些数叫复 振幅 (见1.4和2.5节)。
然而我们必须记住,费曼图中的联络编排并没包含所有信息。我们还需要知道所有粒子的能量和动量。对所有端点(或外)粒子(进来的和出去的),我们可以认为这些量已经给定了,但中间(或内)粒子的能量和动量可以取多个不同的数值,遵从一定的约束,即每个顶点的能量和动量应该恰当地加起来,其中普通粒子的动量等于速度乘以质量,见附录A4和A6。(动量有一个重要的性质,即它是守恒的,于是在任何粒子碰撞过程中,进入的总动量——在矢量和的意义上——必定等于出去的总动量。)于是,尽管我们的叠加看起来很复杂,那只是因为出现在叠加中的系列图越来越复杂,而真实的情形比它复杂多了,因为每个图的内粒子的能量和动量通常会有无限多个可能的数值(在外粒子的值给定情况下)。
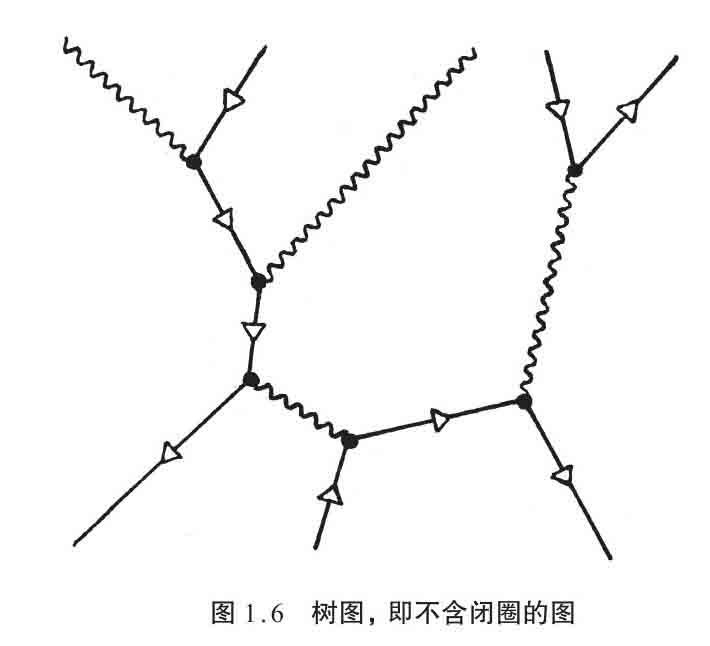
这样,即使单个的费曼图,给定进出粒子,我们也可能需要把无限多个过程加起来。(技术上说,“加起来”将用连续的积分形式,而不是离散的求和,见附录A7和A11,不过其间的差别在这里并不重要。)这种情形出现在费曼图包含 闭圈 的时候,如图1.5的两个例子。对图1.4和1.6那样的树图,没有闭圈,内粒子能量和动量完全由外粒子的值决定。但这些树图没有揭示粒子过程的真正的量子本性,因此我们需要引入闭圈。闭圈的麻烦在于,沿着闭圈的能量-动量是没有限制的,它们可以一圈圈地环绕,因此加起来就会 发散 。
让我们更仔细地来看看。最简单的闭圈情形出现在交换两个粒子的图1.5a。问题的出现是因为,尽管图中每个顶点的能量和动量的三个分量必须恰当地加起来(即进入的量等于出去的量),这并不能提供足够的方程来确定内粒子的量。(对能量-动量的四个分量来说,每一个都有三个独立方程,因为四个顶点的每一个都有守恒方程,但有一个是多余的,只是整个过程的总守恒方程的重复——然而每个分量都有四个独立的未知量,每条内线产生一个,所以没有足够的方程确定未知量,求和必然包含多余的量。)我们在环绕闭圈的过程中总有自由添加(或减去)同一个能量-动量。我们需要把所有这无限多个可能都加起来,就很可能包括越来越大的能量-动量,这就会导致潜在的发散。
于是我们看到,量子法则的直接应用其实很可能给我们带来发散。然而,这并不一定意味着量子场的理论计算的“正确”答案就真的是∞。我们应该记住,如附录A10中的发散级数,虽然直接求和确实产生“∞”,但有时也可以为它赋予有限的结果。QFT的情形虽不尽相同,却也有些相似。为了克服那些无穷的结果,QFT专家几十年来发展了很多计算方法。与A10的例子一样,如果我们够聪明,就能“挖出”一个不能通过简单“加起来”得到的有限答案。相应地,QFT专家们也经常从他们面临的狂野的发散公式中“挤出”有限的结果来,尽管他们运用的很多过程远不像简单的解析延拓那么直接。参见A10(某些“直接”过程也可能落入某些奇怪的陷阱,见3.8节)。
引起很多这些发散——即那些所谓的 紫外发散 ——的一个关键因素,需要在这里指出。那麻烦之所以出现,基本是因为在闭圈的情形中,环绕闭圈的能量和动量的度量是没有限制的,发散就来自越来越高的能量(和动量)被加在一起的贡献。而根据量子力学,非常高能量关联着非常短时间。这主要源自普朗克的著名公式 E=hν ( E 是能量, ν 是频率, h 是普朗克常数),因此高能量值对应于高频率,也就是相继两拍之间的时间间隔很短。同样,巨大的动量值对应于很小的距离。如果想象在很小的时间和距离下时空发生了什么怪事(实际上,多数物理学家都倾向认同这正是量子引力考虑的一个结果),则在允许的能量-动量值的尺度的高端存在一个有效的“截断”。相应地,未来的某个时空结构理论——其中剧烈的变化发生在非常小的时间或距离内——也许确实能将当前源自费曼图闭圈的发散的QFT计算变成有限的。这些时间和距离比普通粒子物理学过程所涉及的尺度要小得多,通常被认为是量子引力理论的相关量所具有的尺度,即普朗克时间(10 -43 秒)和普朗克长度(10 -35 米)(参见1.1节),这些数与粒子过程直接关联的那些常见小数量(如10 -20 )有着同样的意思。
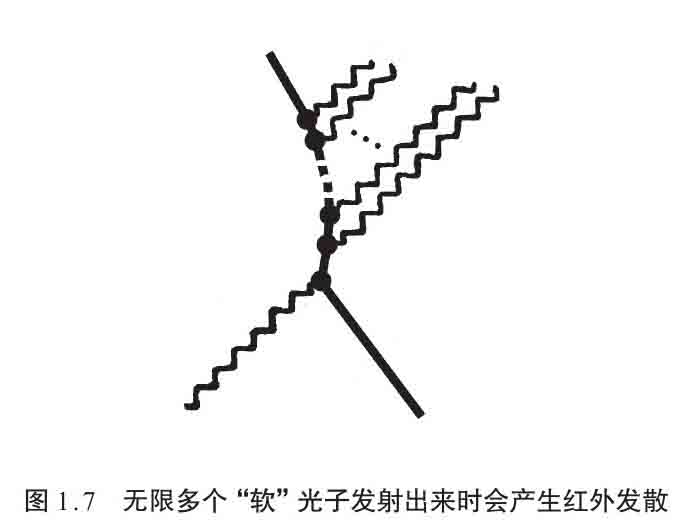
应该指出,QFT还存在所谓的 红外发散 。它们出现在尺度的另一端,能量和动量都非常小,因而牵扯非常大的时间和距离。这些问题与闭圈无关,而与图1.7那样的费曼图有关,其中一个过程可能释放无限多个 软光子 (即能量很小的光子),它们加在一起也会发散。QFT专家们倾向认为红外发散不像紫外发散那么严峻,而且有很多方法(至少暂时地)消除它们。然而,近年来,它们的重要性开始越发显露出来。就眼下的讨论来说,我不想太关注红外发散问题,而想集中说说,QFT如何解决因费曼图闭圈产生的紫外发散问题,弦论的思想又是如何有希望让我们摆脱困境。
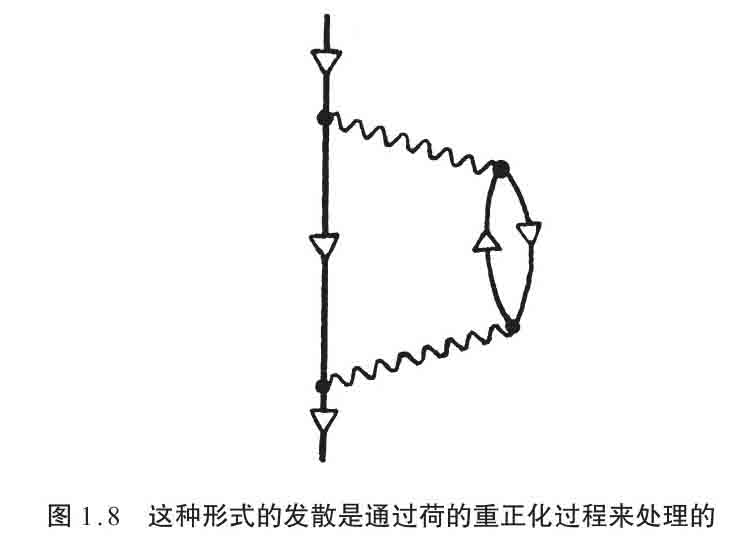
这里特别要注意的是标准的QFT重正化过程。先看看它是如何运作的。根据不同的直接QFT计算,我们得到一个介于粒子的所谓 裸荷 (如电子)与 衣荷 之间的无穷大标度因子,后者也就是我们在实验中实际观测的东西。这是因为图1.8的费曼图所示过程的贡献,它将抑制测量的荷值。问题是,图1.8(和其他很多类似过程)的贡献是“无穷大”(有闭圈)。于是我们看到,为了得到有限的观测值(衣荷),裸荷必须是无限的。这个重正化过程的基本根据是承认QFT在发散出现的极小距离上可能不会完全正确,理论的某个未知的修正或许能补充有限答案所必须的截断。于是,这个过程要我们放弃计算自然的那些真实的度量因子(如粒子的电荷、质量,等等)的努力,而是将QFT强加给我们的所有无限的度量因子聚在一起,接着,我们直接用在实验中观测的裸荷(和质量等)将这些无限的贡献有效地打成整齐的小包,然后忽略它们。令人惊讶的是,对适当的所谓 可重正化的 QFT理论来说,这个过程可以系统地完成,使很多其他QFT计算能获得有限的结果。衣荷(和质量)等数值来自观测而不是来自适当QFT的计算,这些值就得出了那30个参数中的一部分;前面说过,那些参数必须从实验观测值来填补标准模型。
通过上面这些过程,通常可以从QFT得到异常精确数字。例如,现在有一个标准的QFT方法来计算电子的 磁矩 。多数粒子(除了有电荷以外)还表现为一个小磁体,这些粒子的磁矩是其磁性的度量。狄拉克最先直接从他的电子的基本方程(1.1节引介过)预言了电子磁矩,结果与精确的实验观测几乎一样。然而,后来发现数值需要间接来自QFT过程的修正,它们必须包含在直接的单电子效应中。QFT计算的最终结果是狄拉克原先的“纯”预言值的1.001159652…倍[Hanneke et al.2011]。精确得难以置信——正如费曼[1985]说的,这相当于从纽约到洛杉矶的距离确定到一根头发丝!这有力支持了 重正化的 电子和光子的QFT理论(叫 量子电动力学 ,简称QED)——它用狄拉克理论描述电子,用麦克斯韦电磁方程(见1.2节)描述光子,而其相互作用遵从标准的洛伦兹方程(它描述带电粒子对电磁场的响应)。在量子的语境中,后者源自外尔(Hermann Weyl)的 规范程序 (见1.7节)。现在你看到了,理论与观测符合到了异乎寻常的程度,这告诉我们理论存在着某种深层的真实的东西,尽管现在它作为一个数学纲领还未达到完美的和谐。
重正化可以认为是权宜之计,其希望在于,也许最终能发现某个改进形式的QFT,完全不会出现那些无穷大,而且不仅能计算那些尺度因子的有限数值,还能计算不同基本粒子的裸电荷、裸质量等——从而计算它们的实验观测值。人们希望弦论能提供那样的改进QFT,这无疑为那理论增添了动力。但更谨慎、迄今也更成功的方法是,在传统的QFT理论群体中,看重正化过程能在哪个理论下适用,从而选出最有希望的方案。结果表明,只有某些QFT遵从重正化过程——即上面提到的可重正化QFT——而其他的则不行。所以,可重正化性是寻求最有希望QFT的一个有力的选择原理。实际上,人们发现(特别如[’t Hooft 1971;’t Hooft and Veltman 1972]),运用规范理论(1.3节)需要的对称性对产生可重正化的QFT是大有帮助的,这一点也为标准模型的构建提供了强大动力。