




进位计数制(简称进位制)是指用一组固定的数字符号和特定的规则表示数的方法。在人们日常生活和工作中,最熟悉最常用的是十进制,此外还有十二进制、六十进制等。在数字系统和计算机领域,常用的进位计数制是二进制、八进制及十六进制。
研究和讨论进位计数制的问题涉及两个基本概念,即基数和权。在进位计数制中,一种进位制所允许选用的基本数字符号(也称数码)的个数称为这种进位制的基数。不同进位制的基数不同。例如,在十进制中,是选用0~9这10个数字符号来表示的,它的基数是10;在二进制中,是选用0和1这两个数字符号来表示的,它的基数是2;等等。
同一个数字符号处在不同的数位时,它所代表的数值是不同的,每个数字符号所代表的数值等于它本身乘以一个与它所在数位对应的常数,这个常数称为位权,简称权(weight)。例如,十进制数个位的位权是1,十位的位权是10,百位的位权是100,以此类推。一个数的数值大小就等于该数的各位数码乘以相应位权的总和。例如:
十进制数2918=2×1000+9×100+1×10+8×1
十进制数有十个不同的数字符号(0、1、2、3、4、5、6、7、8、9),即它的基数为10;每个数位计满10就向高位进位,即它的进位规则是“逢十进一”。任何一个十进制数,都可以用一个多项式来表示,例如:
312.25=3×10 2 +1×10 1 +2×10 0 +2×10 -1 +5×10 -2
式中,等号右边的表示形式,称为十进制数的多项式表示法,也叫按权展开式;等号左边的形式,称为十进制的位置记数法。位置记数法是一种与位置有关的表示方法,同一个数字符号处于不同的数位时,所代表的数值不同,即其权值不同。容易看出,上式各位的权值分别为10 2 、10 1 、10 0 、10 -1 、10 -2 。
实际的数字系统以及人们日常使用的进位记数制并不仅仅是十进制,其他进位制的计数规律可以看成是十进制计数规律的推广。对于任意的 R 进制来说,它有 R 个不同的数字符号,即基数为 R ,计数进位规则为“逢 R 进一”。
二进制数的基数 R =2,即它所用的数字符号个数只有两个(0和1)。它的计数进位规则为“逢二进一”。
在二进制中,由于每个数位只能有两种不同的取值(要么为0,要么为1),这就特别适合使用仅有两种状态(如导通、截止;高电平、低电平等)的开关元件来表示,一般是采用电子开关元件,目前绝大多数是采用半导体集成电路的开关器件来实现。
对于一个二进制数,也可以用类似十进制数的按权展开式予以展开,例如,二进制数11011.101可以写成:
(11011.101) 2 =1×2 4 +1×2 3 +0×2 2 +1×2 1 +1×2 0 +1×2 -1 +0×2 -2 +1×2 -3
二进制数的一个优点是它只有两种数字符号,因而便于数字系统与电子计算机内部的表示与存储。它的另一个优点是运算规则的简便性,而运算规则的简单,必然导致运算电路的简单以及相关控制的简化。后面将具体讨论二进制算术运算及逻辑运算的规则。
八进制数的基数 R =8,每位可能取8个不同的数字符号0、1、2、3、4、5、6、7中的任何一个,进位规则是“逢八进一”。
由于3位二进制数刚好有8种不同的数位组合(如下所示),所以一位八进制数容易用相应的3位二进制数来表示。
八进制:0 1 2 3 4 5 6 7
二进制:000 001 010 011 100 101 110 111
这样,把一个八进制数每位变换为相等的3位二进制数,组合在一起就成了相等的二进制数。
【 例1.1 】 将八进制数53转换成二进制数。

所以,(53) 8 =(101011) 2 。
显然,用八进制比二进制书写要简短、易读,而且与二进制间的转换也较方便。
十六进制数的基数 R =16,每位用16个数字符号0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F中的一个表示,进位规则是“逢十六进一”。
由于4位二进制数刚好有16种不同的数位组合(如下所示),所以一位十六进制数可以用相应的4位二进制数来表示。
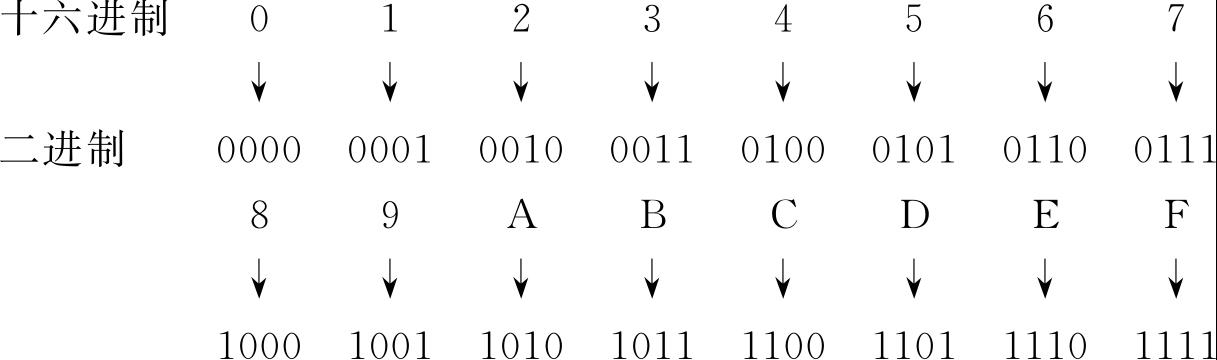
这样,把一个十六进制数的每位变换为相等的4位二进制数,组合在一起就变成了相等的二进制数。
【 例1.2 】 十六进制数转换为二进制数。

所以,(D3F) 16 =(110100111111) 2 。
由上面的介绍可以看出,使用八进制或十六进制表示具有如下的优点:
(1)容易书写、阅读,也便于人们记忆。
(2)容易转换成可用电子开关元件存储、记忆的二进制数。所以,它们是数字系统和计算机中所普遍采用的数据表示形式。