




女士们,先生们:
早在文明发展的原始阶段,人类的头脑中就形成了时空的明确概念,各种各样的事件都发生在时间和空间构成的框架中。这些概念代代相传,从未发生过太大的变化;自精密科学诞生以来,我们开始用数学描述宇宙,时间和空间的概念也顺理成章地融入了这套体系的基础之中。伟大的牛顿可能是第一个明确提出经典时空概念的人,他在《自然哲学的数学原理》中写道:
“从本质上说,绝对的空间与外部的任何事物无关,它始终静止不变。”还有,“从本质上说,绝对的、真实的数学时间始终均匀流逝,与外部任何事物无关。”
人们对这套经典的时空观深信不疑,哲学家常常将它当作先验的真理,甚至没有任何一位科学家想过对它提出质疑。
不过,到了20世纪初,人们通过最精密的物理实验方法观测到了许多经典时空观无法解释的矛盾结果。当代最伟大的物理学家阿尔伯特·爱因斯坦由此提出了一个革命性的想法:如果抛开传统的束缚,我们没有任何理由认为经典时空观就一定是对的,为了适应最新、最精密的观测结果,原有的概念必须做出修正。事实上,经典时空观基于人类的日常体验,而当代的精密观测手段基于先进的实验技术,由此得出有悖于“常识”的新结果也不足为奇;这些最新的观测结果表明,我们原来的时空观过于粗糙,一点儿也不精确,它之所以能满足日常生活和物理学发展早期阶段的需求,仅仅因为它和真正正确的概念相差甚微。我们同样不必感到惊讶的是,现代科学的飞速发展引领我们走进了全新的领域,在这个世界里,经典时空观和真理之间的区别被放大到了无法忽视的程度,旧的概念根本无法解释新的现象。
我们发现了一个彻底动摇经典时空观的最重要的实验结果:真空光速代表着所有物理速度的可能上限。这个重要但却出乎意料的结论主要来自美国物理学家迈克耳孙(Michelson)的实验。19世纪末,迈克耳孙试图观察地球的运动如何影响光传播的速度,结果他(和整个科学世界)惊讶地发现,地球运动完全不会影响光的传播,真空光速始终恒定不变,彻底独立于任何参考系和光源的运动。不用说,这个结果非常惊人,而且完全不符合运动最基本的概念。事实上,如果你高速迎向某件在空间中高速运动的物体,那么该物体将以更大的相对速度与你相撞,这个速度应该等于物体与观测者的速度之和。从另一方面来说,如果你试图逃离这件物体,那么它将从背后以更小的速度击中你,你们之间的相对速度等于二者的速度之差。
同样地,如果你坐在一辆运动的汽车里,迎面驶向空气中的一道声波,那么你在车中测量到的音速应该等于实际音速加上车速;但要是汽车的行驶方向和声波的传播方向相同,那么你测量到的音速等于实际音速减去车速。这就是速度的加法定理,我们通常认为它是一条不证自明的真理。
但是,最精密的实验表明,速度的加法定理无法应用于光,无论观测者以什么速度运动,真空中的光速始终是恒定的每秒300000千米(我们通常用符号c来指代这个值)。
“好吧,”你也许会说,“难道我们就不能通过物理手段获得几个比较小的速度,然后把它们统统加起来,最终得到超过光速的结果吗?”
比如说,我们可以设想一辆跑得很快的火车。假设火车的运动速度等于光速的四分之三,与此同时,车顶上有一位流浪汉沿着车厢向前奔跑,他的速度同样是光速的四分之三。
根据加法定理,流浪汉和火车的速度加起来等于1.5倍光速,所以这个人应该跑得比一盏灯射出的光束还快。但事实上,因为我们已经通过实验证明了光速恒定,所以流浪汉的实际速度必然小于我们的预期——它不可能超过临界值c,因此我们可以得出结论,对于那些更小的速度而言,加法定理肯定也有问题。
我不想用数学形式来阐述这个问题,你只需要知道,计算两个运动物体叠加速度的新公式其实非常简单。
如果你想知道v 1 和v 2 两个速度之和,那么可以利用下面这个公式:
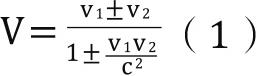
通过这个公式我们可以看到,如果两个初始速度都很小,我是说远小于光速,那么公式(1)中分母的第二个项小得可以忽略不计,我们最终得到的结果和经典的加法定理完全相同。但是,如果v
1
和v
2
的值比较大,那么公式(1)算出的结果必然小于二者的算术和。举个例子,说回刚才那个在火车顶上奔跑的流浪汉,
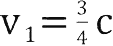 ,
,
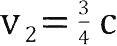 ,根据公式计算得出,
,根据公式计算得出,
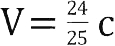 ,仍然小于光速。
,仍然小于光速。
特定情况下,如果某个初始速度正好等于光速c,那么不管第二个速度是多少,公式(1)算出的结果始终等于c。因此,你无论将多少个速度叠加在一起都不可能超过光速。
你或许还愿意知道,这个公式已经得到了实验验证,我们的确发现,两个速度叠加的结果始终小于它们的算术和。
知道了速度上限的存在,我们可以开始试图挑战经典的时空观,眼下的第一个目标就是基于经典时空观的“同时”的概念。
当你说出“开普敦附近的矿场发生爆炸的时候,你正好在伦敦的公寓里吃火腿和鸡蛋”这句话的时候,你觉得你完全明白自己在说什么。但我很快就会向你证明,其实你不明白;严格说来,这句表述没有确切的意义。事实上,你打算用什么办法来检验不同地点的两个事件是否同时发生呢?你大概会说,两个地方的钟显示的时间一样啊。但接下来我们就要问了:你如何保证不同地点的两口钟在同一时间显示的数值就真的完全一样呢?于是我们又回到了最初的那个问题。
真空中的光速完全不受参考系和光源运动的影响,基于这个最明确的事实,要测量距离、正确设置不同观测点的时钟,下面我介绍的方法应该是最合理的,仔细思考之下你会发现,实际上这也是唯一合理的办法。
一个光信号从A点传往B点,B点收到信号以后立即将它送回A点。这样一来,AB之间的距离应该等于A点收发信号间隔时间的一半乘以常数光速。
如果光信号到达B点时,B点的时钟显示的时间等于A点收发信号时间的中值,那么我们可以说,A点和B点的时钟显示的时间完全相同。利用火箭上两个不同的观测点,我们最终建立了一个理想的参考系,从此以后,我们可以回答不同地点的两个事件是否同时发生(或者时间间隔是多少)的问题。
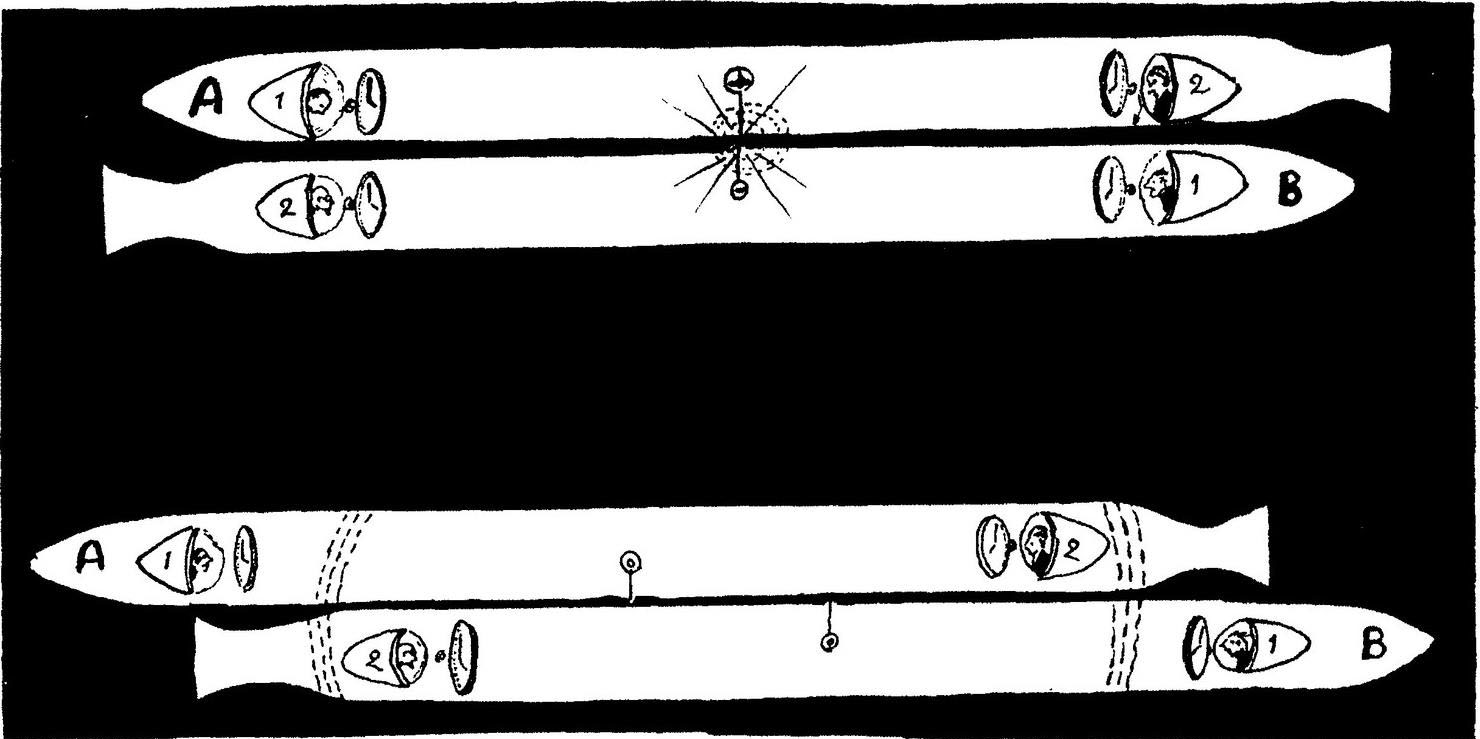
两个反向运动的平台
但其他参考系下的观测者是否认可这个结果呢?要回答这个问题,我们不妨在两个不同的火箭上分别建立一个参考系,例如两枚以恒定速度反向运动的长火箭,现在我们可以看看,这两个参考系如何互相验证。假设四位观测者分别位于两枚火箭的头部和尾部,首先,他们试图对表。每对观测者都可以利用我们上面描述的办法来对表,比如说,他们可以从火箭中点(利用尺子测量确定)发射一个光信号,当这个信号到达火箭两端时,观测者将时间设为零。如上所述,每对观测者就此定义了自身系统内部的同时性,当然,从他们自己的角度来看,他们的表都“对好了”。
现在,他们决定观察一下另一枚火箭上的时间和自己这边是否相同。比如说,两枚火箭擦肩而过的时候,不同火箭上的两位观测者的表显示的时间一样吗?要回答这个问题,我们可以采用下面的办法:在两枚火箭的几何中点分别放置一个带电导体,火箭擦肩而过的时候,两个导体之间会产生电火花,因此两个光信号将从两枚火箭的中点分别传向它的头部和尾部。光信号速度恒定,所以当它分别到达几位观测者所在的位置时,火箭的相对位置必然已经发生变化,2A和2B两位观测者与光源之间的距离比1A和1B更近。
显然,光信号到达观测者2A所在的位置时,观测者1B还没收到信号,所以光信号需要花费更多的时间才能传到1B的位置。因此,如果1B将自己收到信号的时间设为零点,那么观测者2A一定会认为他的表慢了。
基于同样的道理,观测者1A也会认为2B(后者收到信号的时间比他早)的表快了。按照他们对同时性的定义,每个人都认为自己的表是准的,火箭A上的观测者会认为火箭B上的两位观测者的表显示的时间不一样。可是别忘了,出于同样的原因,火箭B上的观测者觉得自己的表是准的,火箭A上那两位观测者的表才有问题。
由于两枚火箭完全相同,要平息两组观测者的争端,我们只能说,从他们自己的角度来看,两组观测者都是对的,但谁才是“绝对”正确的呢?从物理学的角度来说,这个问题没有意义。
这些冗长的讨论恐怕已经让你累得够呛,但如果仔细听完,你会清晰地发现,只要采用我们刚才描述的方法来测量空间和时间,绝对同时性的概念就会消失,哪怕你在某个参考系内观察到不同地点的两个事件同时发生,只要换个参考系,你就会发现二者之间其实存在一定的时间间隔。
乍听之下,这个说法似乎十分无稽,但我可以换个说法:假设你在火车上吃饭,虽然在喝汤和吃甜点的时候,你一直坐在餐车上的同一个位置,但这两个点投射到铁轨上的位置却相隔甚远,这样听起来是不是就正常多了?用物理语言来描述的话,这就是某个参考系内不同时间发生在同一地点的两个事件换到另一个参考系下就会产生一定的空间间隔。
比较一下现在这个“啰唆”的描述和前面那个“矛盾”的描述,你会发现它们完全对称,只需要把“时间”和“空间”互换一下,二者的表述完全相同。
这就是爱因斯坦的完整观点:尽管从经典物理学的角度来看,时间完全独立于空间和运动,“始终均匀流逝,与外部任何事物无关”(牛顿),但根据新的物理理论,空间和时间关系紧密,它们不过是同一个“时空连续统一体”(所有可观测的事件都发生在这个系统内)中两条互相垂直的坐标轴而已。将这个四维连续统一体切割为三维空间与一维时间的做法完全出于主观,具体取决于你采用的参考系。
如果从某个参考系的角度观察,空间距离为l的两个事件在时间轴上的间隔为t,那么只要换个参考系,同样两个事件的空间距离和时间间隔就会变成l'和t'。因此,从某种意义上说,我们可以认为时间和空间可以相互转换。很容易理解,对我们来说,为什么时间转化为空间十分简单(比如在火车上吃饭),但要把空间转化为时间(相对的同时性),感觉就很别扭。问题的关键在于,如果我们以厘米为单位来衡量距离,那么对应的时间单位不应该是常用的“秒”,而是另一个“合理的时间间隔”,它代表的是光信号行经1厘米的距离需要的时间,也就是0.00000000003秒。
因此,在我们日常经验的范围内,要把空间间隔转化为时间间隔,最终得到的结果小得根本无法觉察,这似乎支持了经典的观点:时间绝对独立于其他因素,不可改变。
但是,如果我们的研究对象运动速度极快,比如说,要研究放射性物体释放的电子的运动,或者原子内部的电子运动,那么这些物体在“合理的时间间隔”内行经的距离正好和时间间隔数量级相当,因此我们必须将上面提到的两种效应都纳入考虑,相对论也变得尤为重要。哪怕物体运动速度相对较小,例如太阳系内行星的运动,我们也可以通过高精度的天文测量手段观察到相对论效应,但这需要以每年几分之一角秒的精度来测量行星运动的变化。
我一直试图向你解释的是,对经典时空观的质疑引领我们得出了一个结论:空间距离可以部分转化为时间间隔,反之亦然;这意味着同一段距离或时间的数值在不同的运动系下可能有所差异。
这个问题有一套比较简单的数学解释,但我不打算在这里详细介绍,总而言之,利用这套数学方法,我们建立了时空转化的具体公式。假设某件长度为l的物体相对于观测者的运动速度为ν,那么观测者测得的物体长度必然缩短,具体取决于它的运动速度,最终测得的长度计算方式如下:
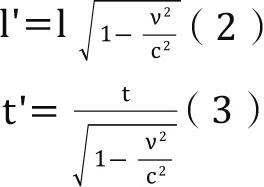
类似的,任何需要花费时间t的过程在相对运动的参考系下花费的时间都会变长,最终测得的时间t'如公式(3)所示。这就是相对论中著名的“空间缩短”和“时间膨胀”。
一般来说,如果ν远小于c,那么这两种效应微乎其微;但要是速度相对较大,我们在运动参考系下观察到的长度可能缩短到任何程度,时间间隔也可能变得非常非常长。
我希望你不要忘记,这两种效应都是绝对对称的,飞驰火车上的乘客会好奇静止车厢里的人为什么那么瘦,走得又那么慢;与此同时,静止车厢里的人也对运动火车上的乘客有同样的疑惑。
速度上限的存在还带来了另一个重要的后果:运动物体的质量会发生变化。
根据通用的基础力学,物体的质量越大,你就越难让它从静止状态开始运动,或者改变它的既有运动速度。
任何物体在任何条件下都不可能超过光速,基于这个事实,我们可以直接得出结论:随着物体的速度不断接近光速,它抵抗进一步加速的能力——换句话说,它的质量——必然无限增大。我们可以用数学方法来描述物体质量和运动速度的关系,最终得到一个类似(2)和(3)的公式。如果某个物体在极低的速度下质量为m 0 ,那么速度为ν的时候,它的质量m计算方式如下:
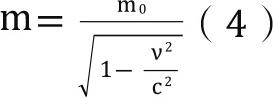
当ν接近c的时候,物体抵抗进一步加速的能力将变得无限大。我们可以通过高速运动的粒子轻松观察到这种质量变化的相对论效应。比如说,放射性物体释放的电子质量(其速度等于光速的99%)比静止状态的电子大好几倍,而组成所谓的宇宙射线的电子质量(它们的运动速度通常相当于光速的99.98%)更是大得离谱。在这样的速度下,经典力学毫无用武之地,我们完全走进了相对论的王国。