




“你们会猜谜吗?”马先生出乎大家意料地提出这么一个问题,大概是因为问题来得突兀的缘故,大家都默然。
“据说从前有个人出了一个谜给人猜,那谜面是一个‘日’字,猜杜诗一句,你们猜是什么句子?”说完,马先生便呆立着望向大家。
没有一个人回答。
“无边落木萧萧下,”马先生说,“怎样解释呢?这就说来话长了,中国在晋以后分成南北朝,南朝最初是宋,宋以后是萧道成所创的齐,齐以后是萧衍所创的梁,梁以后是陳霸先所创的陳。‘萧萧下’就是说,两朝姓萧的皇帝之后,当然是‘陳’。‘陳’字去了左边是‘東’字,‘東’字去了‘木’字便只剩‘日’字了。这样一解释,这谜好像还真不错,不过出谜的人倒是‘妙手偶得之’,而猜的人却只好暗中摸索了。”
虽然这是一件有趣的故事,但我,也许不只我,始终不明白马先生在讲算学时突然提到它有什么用意,只得静静地等待他的讲解了。
“你们觉得我提出这故事有点儿不伦不类吗?其实,一般教科书上的习题,特别是四则应用问题一类,倘若没有例题,没有人讲解、指导,对于学习的人,也正和谜面一样,得靠自己去摸索,只是努力程度不同罢了。摸索本来不是正当办法,所以处理一个问题,必须有一定的步骤。第一,就是要理解问题中所包含而没有提出的事实或算理的条件。
“例如这次要讲的年龄的关系的题目,大体可分两种,即每题中或是给出两个以上的人的年龄,求他们的从属关系成立的时间,或是给出他们的年龄或从属关系而求得他们的年龄。
“但这类题目包含着两个事实以上的条件,题目上总归不会提到的:其一,两人年龄的差是从他们出生起就一定不变的;其二,每多一年或少一年,两人便各长一岁或小一岁。不懂得这个事实,这类的题目便难于摸索了。这正如上面所说的谜语,别人难于索解的原因,就在不曾把两个‘萧’,看成萧道成和萧衍。话虽如此,毕竟算学不是猜谜,只需留意题上没有明确提出的,而事实上存在的条件,就不至于暗中摸索了。闲言表过,且提正文。”
例一:当前,父亲三十五岁,儿子九岁,几年后父亲年龄是儿子年龄的三倍?
写好题目,马先生说:“不管三七二十一,我们先把表示父和子的年岁的两条线画出来。在图上,横轴表示岁数,纵轴表示年数。父现在三十五岁,以后每过一年增加一岁,用 AB 线表示。儿子现在九岁,以后也是每过一年增加一岁,用 CD 线表示。
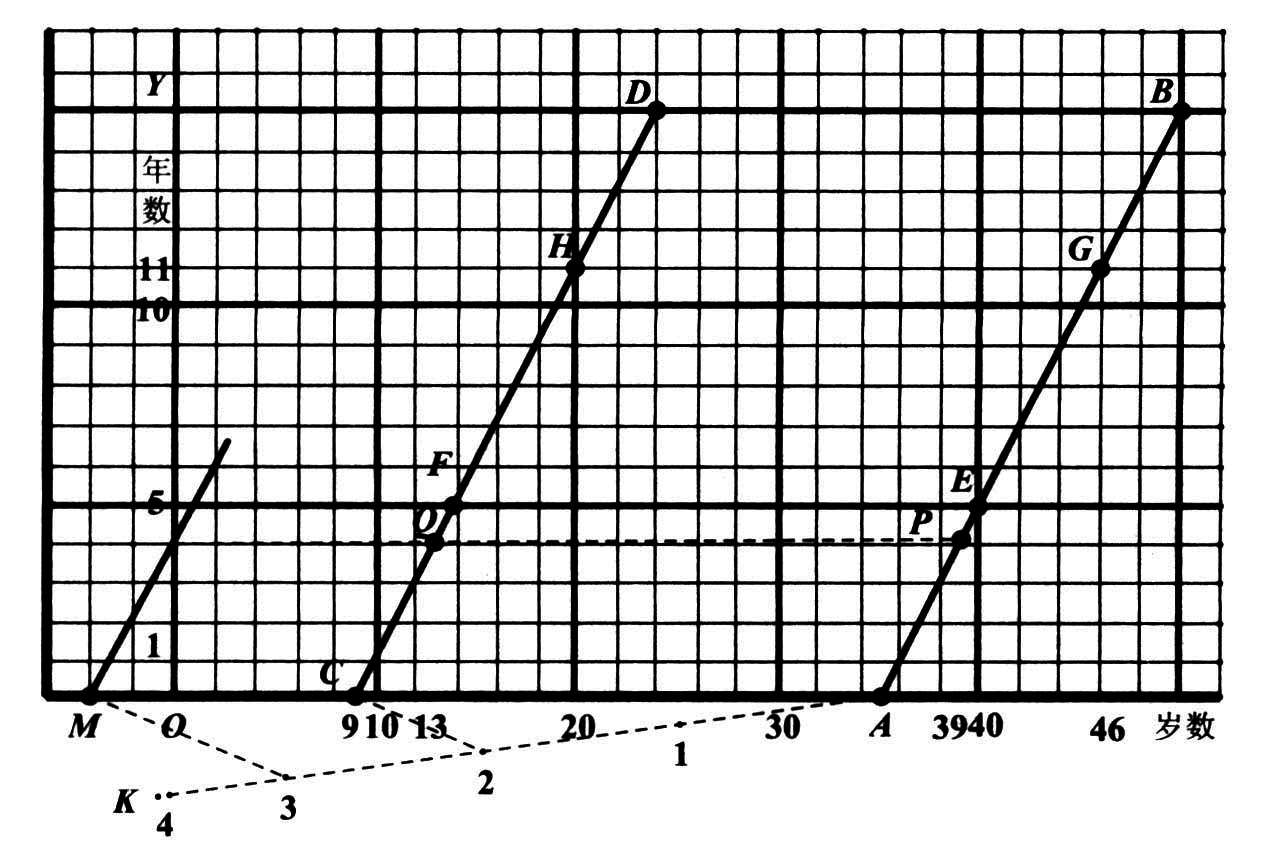
图 35
“过五年,父亲几岁?儿子几岁?”
“父亲四十岁,儿子十四岁。”这是谁都能回答上来的。
“过十一年呢?”
“父四十六岁,子二十岁。”这也是谁都能回答上来的。
“怎样看出来的?”马先生问。
“从 OY 线上记有 5 的那点横看到 AB 线得 E 点,再往下看,就得四十,这是五年后父的年龄。又看到 CD 线得 F 点,再往下看得十四,就是五年后子的年龄。”我回答。
“从 OY 线上记有 11 的那点横看到 AB 线得 G 点,再往下看,就得四十六,这是十一年后父的年龄。又看到 CD 线得 H 点,再往下看得二十,就是十一年后子的年龄。”周学敏抢着回答,并且故意学着我的语调。
“对了!”马先生高声说,突然愣住。
“5 E 是 5 F 的 3 倍吗?”马先生问后,大家摇摇头。
“11 G 是 11 H 的 3 倍吗?”仍是一阵摇头,不知为什么今天只有周学敏这般高兴,扯长了声音回答:“不——是——”
“现在就是要找在 OY 上的哪一点到 AB 的距离是到 CD 的距离的3倍了。当然我们还是应当用画图的方法,不可硬用眼睛看。等分线段的方法,还记得吗?在讲除法的时候讲过的。”
王有道说了一段等分线段的方法。
接着,马先生说:“先随意画一条线 AK ,从 A 起在上面取 A 1,12,23 相等的三段。连 C 2,过 3 作线平行于 C 2,与 OA 交于 M 。过 M 作线平行于 CD ,与 OY 交于 4,这就得了。”
四年后,父年三十九岁,子年十三岁,正是父年三倍于子年,而图上的 4 P 也恰好 3 倍于 4 Q ,真是奇妙!然而为什么这样画就行了,我却不太明白。
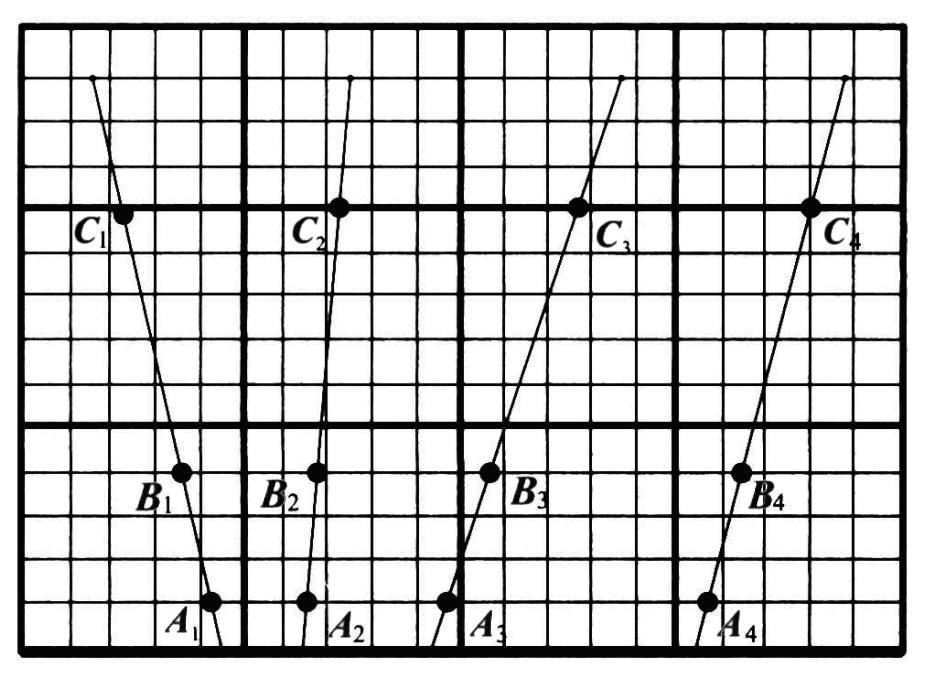
图 36
马先生好像知道我的心事似的,说:“现在,我们应当考求这个画法的来源。”他随手在黑板上画出上图,要我们看了后回答 B 1 C 1 , B 2 C 2 , B 3 C 3 , B 4 C 4 ,各对于 A 1 B 1 , A 2 B 2 , A 3 B 3 , A 4 B 4 的倍数是否相等。当然,谁都看得出来这倍数都是 2。
大家回答了以后,马先生说:“这就是说,一条线被平行线分成若干段,无论这条线怎样画,这些段数的倍数关系都是相同的。所以 4 P 对于 4 Q ,和 MA 对于 MC ,也就和 3 A 对于 32 的倍数关系是一样的。”
这样讲我就明白了。
“假如,题上问的是 6 倍,怎么画?”马先生问。
“在 AK 上取相等的 6 段,连 C 5,画 6M平行于 C 5。”王有道回答。这,现在我也明白了,因为无论 OY 到 AB 的距离是 OY 到 CD 距离的多少倍, OY 到 CD ,都是这距离的一倍,因而总是将AK上的倒数第二点和C相连,而过末一点作线和它平行。
至于这题的算法,马先生叫我们据图加以探究,我们看出CA是父子年龄的差,和 QP , FE , HG 全一样。而当 4 P 是 4 Q 的 3 倍时, MA 也是 MC 的 3 倍,并且在这地方 4 Q 、 MC 都是所求的若干年后的子年。因此得下面的算法:

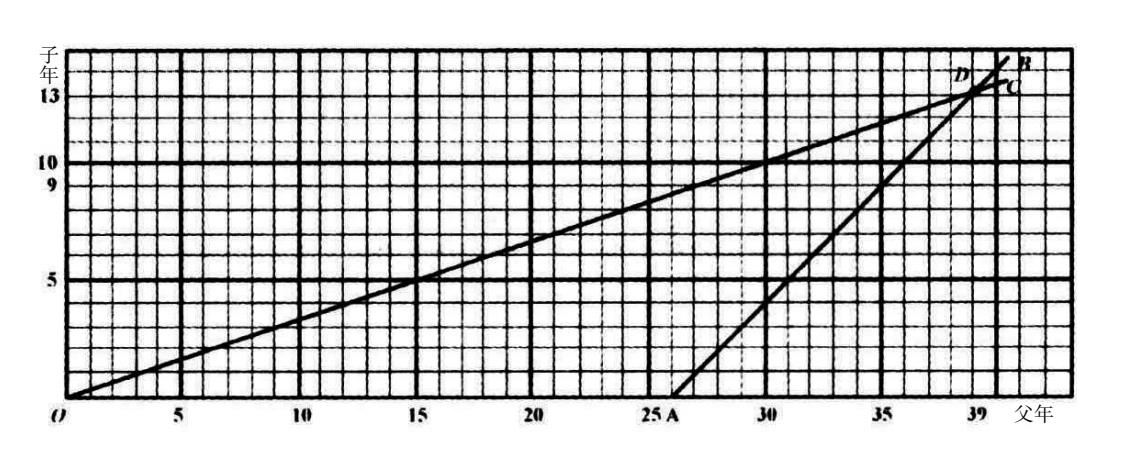
图 37
讨论完毕以后,马先生一句话不说,将图 37 画了出来,指定周学敏去解释。
我倒有点儿幸灾乐祸的心情,因为他曾学过我,但事后一想,这实在无聊。他的算学虽不及王有道,这次却讲得很有条理,而且真是简单明了。下面的一段,就是周学敏讲的,我一字没改记在这里以表忏悔!
别解:
“父年三十五岁,子年九岁,他们相差二十六岁,即这个人二十六岁时生这儿子,所以他二十六岁时,他的儿子是零岁。以后,每过一年,他大一岁,他的儿子也大一岁。依差一定的表示法,得 AB 线。题上要求的是父年 3 倍于子年的时间,依倍数一定的表示法得 OC 线,两线相交于 D 。依交叉原理, D 点所示的,便是合于题上的条件时,父子各人的年岁:父年三十九,子年十三。从三十五到三十九和从九到十三都是四,即四年后父年正好是子年的三倍。”
对于周学敏的解说,马先生也非常满意,他评价了一句:“不错!”然后写出例二。
例二:当前,父年三十六岁,子年十八岁,几年后父年是子年的三倍?
这题看上去和例一完全相同。马先生让我们各自依样画葫芦,但一动手,便碰了钉子,过 M 所画的和 CD 平行的线与 OY 却相交在下面 9的地方。这是怎么一回事呢?
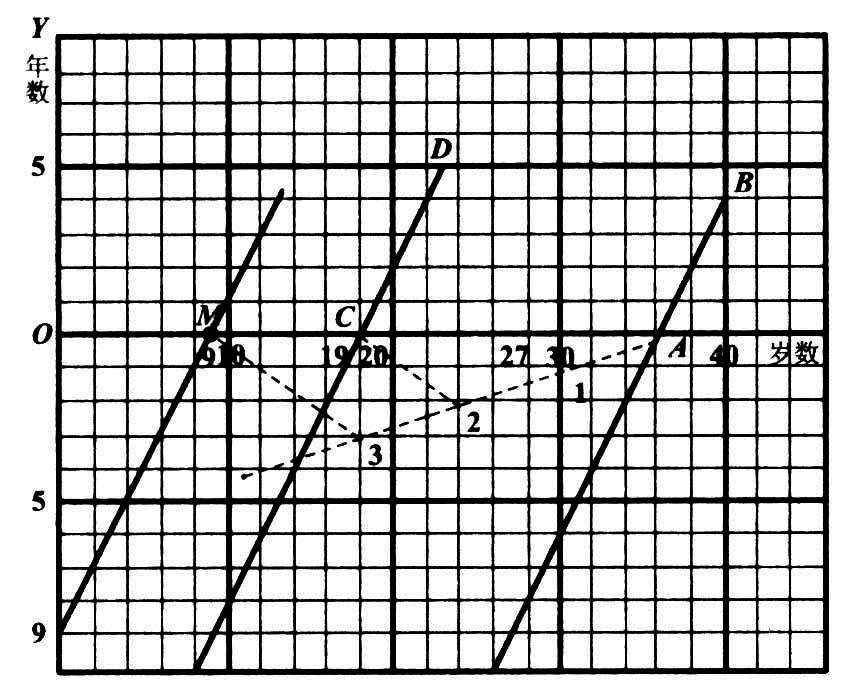
图 38
马先生始终一声不吭,让我们自己去做。后来我从这 9 的位置横看到 AB ,再竖看上去,得父年二十七岁;而看到 CD ,再竖看上去,得子年九岁,正好父年是子年的三倍。到此我才领悟过来,这在下方的9,表示的是九年以前。而这个例题完全是马先生有意弄出来的。这么一来,我还知道几年前或几年后的算法全是一样,只是减的时候,被减数和减数不同罢了。本题的计算应当是:

我试用别的解法做,得图39, AB 和 OC 的交点 D ,表明父年二十七岁时,子年九岁,正是三倍,而从三十六回到二十七恰好九年,所以本题的解答是九年以前。
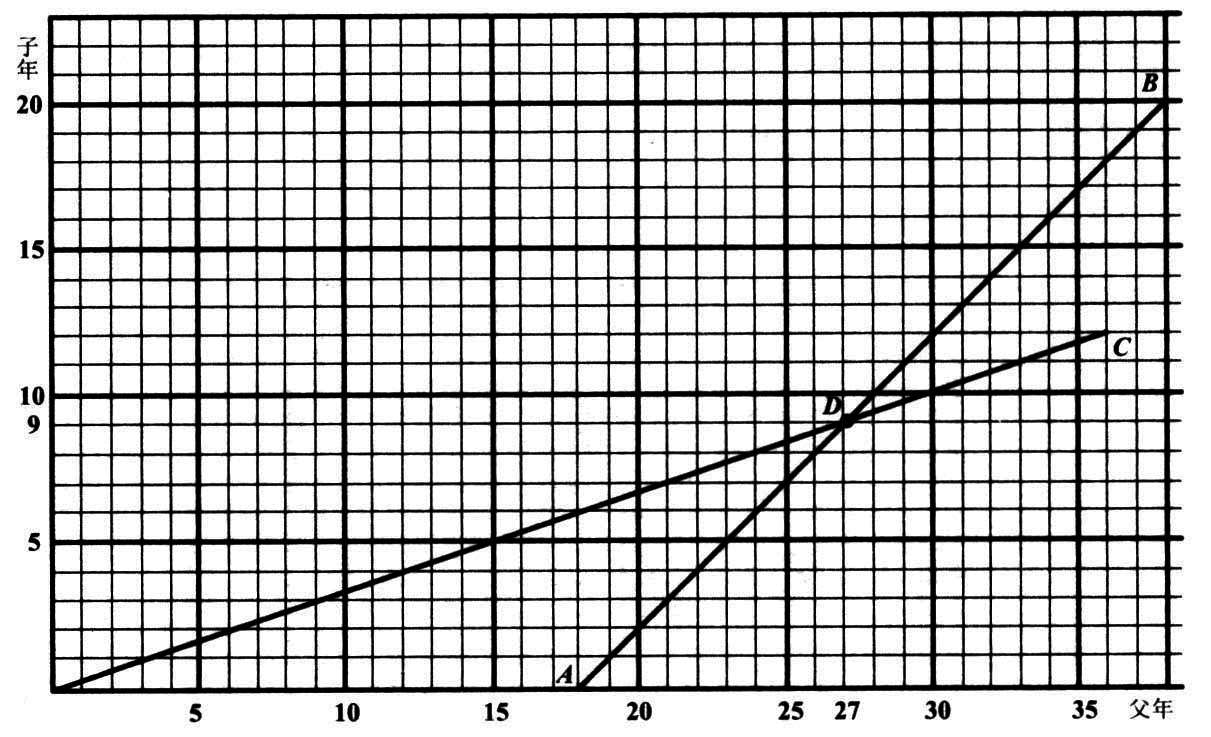
图 39
例三:当前,父年三十二岁,一子年六岁,一女年四岁,几年后,父的年龄与子女二人年龄的和相等?
马先生问我们这个题和前两题的不同之处,这是略一——我现在也敢说“略一”了,真是十分欣幸!——思索就知道的,父的年龄每过一年只增加一岁,而子女年龄的和每过一年却增加两岁。所以从现在起,父的年岁用AB线表示,而子女二人年岁的和用 CD 表示。
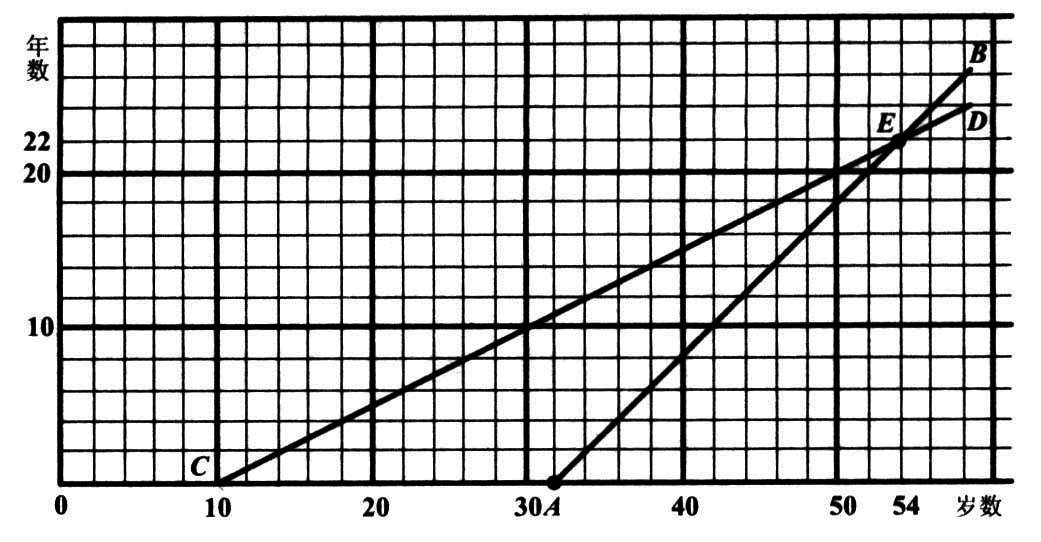
图 40
AB 和 CD 的交点E,竖看是五十四,横看是二十二。从现在起,二十二年后,父年五十四岁,子年二十八岁,女年二十六岁,相加也是五十四岁。
至于本题的算法,图上显示得很清楚。 CA 表示当前父的年岁同子女俩的年岁的差,往后看去,每过一年这差就减少一岁,少到了零,便是所求的时间,所以:

这题有没有别解,马先生不曾说,我也没有想过,反而是王有道将它补出来的:
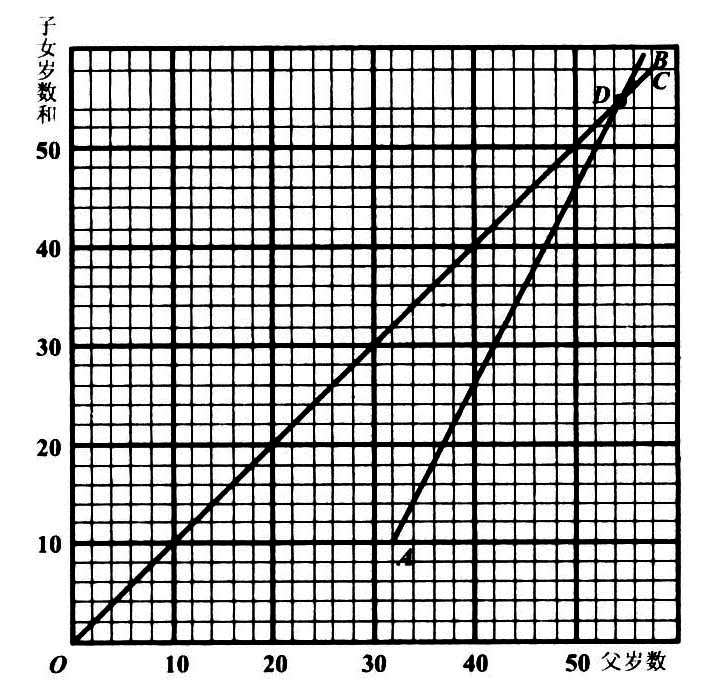
图 41
AB 线表示现在父的年岁同着子女俩的年岁,以后一面逐年增加一岁,而另一面增加二岁, OC 表示两面相等,即一倍的关系。这都容易想出。只有 AB 线的 A 不在最末一条横线上,这是王有道的巧思,我只能佩服了。据王有道说,他第一次也把 A 点画在三十二的地方,结果不符。仔细一想,才知道错得十分可笑。原来那样画法,表示的是父年三十二岁时,子女俩年岁的和是零。由此他想到子女俩的年岁的和是十,就想到 A 点应当在第五条横线上。虽是如此,但我依然佩服!
例四:当前,祖父八十五岁,长孙十二岁,次孙三岁,几年后祖父的年岁是两孙的三倍?
这例题是马先生留给我们做的,参照了王有道的补充前题的别解,我也得出它的图来了。因为祖父年八十五岁时,两孙共年十五岁,所以得 A 点。以后祖父加一岁,两孙共加两岁,所以得 AB 线。 OC 是表示定倍数的。两线的交点 D ,竖看得九十三,是祖父的年岁;横看得三十一,是两孙年岁的和。从八十五到九十三有八年,所以得知八年后祖年岁是两孙年岁的三倍。
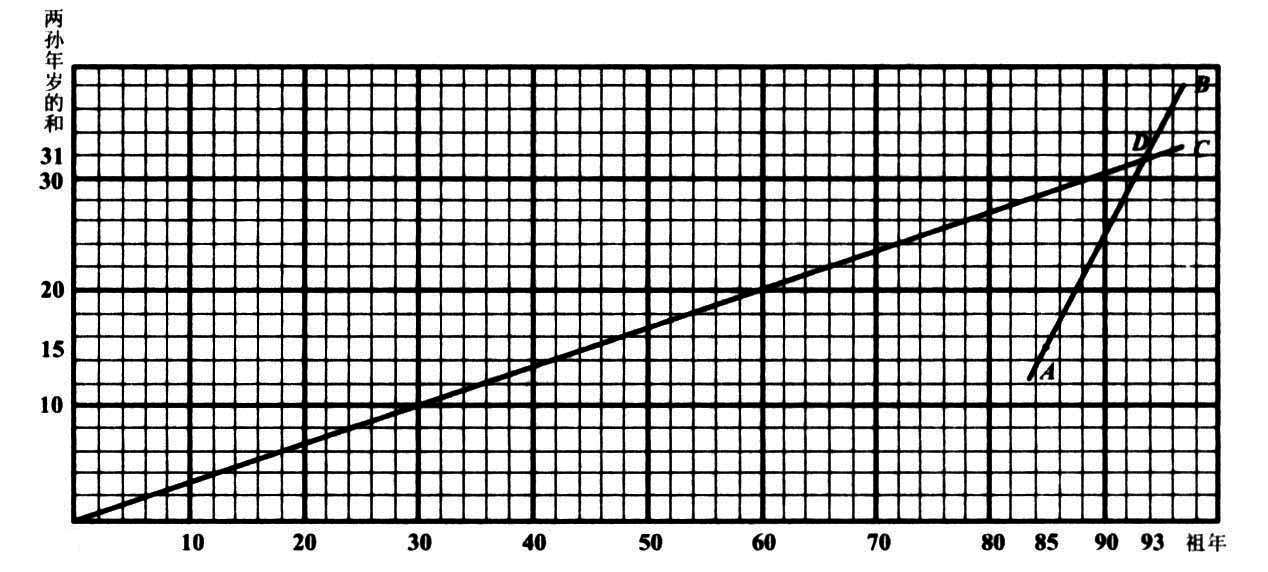
图 42
本题的算法,是我曾经在一本算学教科书上见到的:[85-(12+3)×3]÷[2×3-1]=(85-45)÷5=8
它的解释是这样:就当前说,两孙共年(12+3)岁,三倍是(12+3)×3,比祖父的年岁还少[85-(12+3)×3],这差出来的岁数,就需由两孙每年比祖父多加的岁数来填补。两孙每年共加两岁,就三倍计算,共增加2×3岁,减去祖父增加的一岁,就是每年多加(2×3-1)岁,由此便得出上面的计算法。
这算法能否由图上得出来,以及本题照前几例的第一种方法是否可解,我们没有去想,也不好意思去问马先生,因为这好像应该自己用点儿心去回答,只得留待将来了。