




牛顿曾经用微粒的方式来解释光的性质。特别是,光沿直线传播的这个证据告诉他,光不可能是波——任何一个曾经向池塘投过石子,并看到波浪向外扩散传播的人,都知道波是不会直线传播的。一个明显的例子是,要知道光线是多么的直行,看一下阴影就很清楚了,因为光线不能绕到被照亮物体的背面,所以背面没有光到达,这就形成了阴影。甚至能穿越整个空间的太阳光,当月亮经过其路径而产生日食期间,也会在地球表面形成边缘十分锐利清晰的阴影。
然而,托马斯·杨和菲涅耳发现,光的行为的确就像是波动,但仅是在这些案例难以察觉的更细微的尺度上如此。关键性的实际实验,包括让光穿过屏幕上两个非常狭窄的缝隙,将通过狭缝的光线投射到另一块屏幕上。在第二块屏幕上所产生的明暗条纹样式说明,光已经作为波动从两个缝隙中传播过来了,并且两束光波之间互有干涉,正如同时在一个池塘中投下两块石头所产生的两组波动互相干涉一样。干涉效应之所以不那么显而易见的原因,在于光的波长只有大约1/3000厘米,比池塘里最小的涟漪还要微小。因此,若使用足够精确的测量设备,就能够看到一部分光线是如何绕过物体的边缘而填充到其阴影的地方——被光所投照的物体有着像刀片一样非常尖锐的边缘。
在18世纪20年代,当牛顿去世的时候,几乎所有的科学家都认为光是由粒子流组成的。而到了19世纪20年代,当拉普拉斯去世时,几乎所有的科学家又都相信,光是波动的一种形式。19世纪后期,詹姆斯·克拉克·麦克斯韦(James Clerk Maxwell)发展了一组方程来描述这些波动如何以电磁振荡的方式在空间中传播。变化着的电波激发出变化的磁波,变化的磁波又接着激发出变化着的电波,于是这些波就运动起来。当麦克斯韦创建他的方程组(它们解释了无线电波的行为,已经知道这种波也产生于电磁效应)时,他发现该方程能自动地生成电磁波的速度,而且方程所生成的速度就是光速。再没有比这更令人信服的证据了,服从麦克斯韦方程组的光和无线电波都是波动。
20世纪初,当阿尔伯特·爱因斯坦指出,光的某些性质仍然而且只能用粒子的方式解释时,许多物理学家都像被电击了一样震惊。特别是在1905年,他提出,一束光线能将电子从金属表面撞击出来(光电效应),是由于连续不断的光粒子的作用所致,这就完全等同于牛顿的微粒说了。纯粹的波乃至电磁波,都无法简单地做到这一点。爱因斯坦的工作,促使人们重新审查了光的性质,从而导致了一个令人目瞪口呆的结论,光只能被理解为一种复合体,它既是波,也是粒子,现在被称为光子。1921年,爱因斯坦因为这一工作而获得了诺贝尔物理学奖。因此,到20世纪20年代,仅仅就在牛顿去世的短短200年后,物理学家们就相信牛顿和杨都是对的,光既是粒子也是波。
这种波粒二象性的影响远远超出了光的研究。它是量子理论的基石,该理论在亚原子水平上描述了世界的行为。20世纪20年代所进行的一些实验发现,以前一直被认为是粒子的电子和其他物质实体,也具有波动性特征。现在已经很清楚了,这种波粒二象性适用于所有的实体,虽然它仅仅是在分子和原子的尺度上具有重要意义。即使如此,正如我们将要看到的,量子效应也会影响到黑洞的行为。
光具有二象性这一发现,并没有破坏麦克斯韦方程的有效性。光仍然是波,同时也是粒子。特别是为了某些目的,例如,解释光电效应,把光设想成由光子组成的会更加方便,而这些光子按照麦克斯韦方程的要求,仍然是以光速在传播。但当光离开某个恒星时,该方程并不允许它在引力的影响下放缓其传播速度——甚至在米歇尔暗星的巨大表面引力影响下也不行。换言之,引力不能使光子加速。爱因斯坦意识到,麦克斯韦方程与牛顿运动定律是不相容的,他创建了狭义相对论(也是在1905年)来解决这个难题。
狭义相对论的基础是这样一个事实,无论在哪儿测量,也无论测量或被测量者多么快速(在任何方向)的移动,光在空间中传播的速度始终都是相同的。这个理论还认为,所有以自己的某个固定速度移动着的观察者,相对于彼此都同样有权认为自己处于静止状态,而其他观察者处于运动状态。它解释了相对于静止的观察者,为何移动的时钟会变慢(因为时间本身被运动减缓了),运动的尺子会收缩,移动中的物体质量会增加。它还告诉我们,能量和质量是可以互换的,而且,最重要的是在目前情况下,没有什么物体可以超光速运行。换句话说,如果米歇尔和拉普拉斯所设想的那类暗星确实存在,则任何东西都无法逃离它们。重要的是要认识到,所有这些效应,已经被涉及快速运动粒子的直接实验所验证和测量过了。狭义相对论的确有些违反了我们的常识,这是因为相对论效应仅在接近光速的时候才会变得更加重要,而我们的常识则来自低速的世界。
但爱因斯坦意识到他还没有一个如牛顿在其《原理》中所提出的那样完整的宇宙理论,因为他的狭义相对论只处理常速运动,而不涉及变速运动。为了描述变速运动和引力,他创立了广义相对论,其完整形式发表于1916年。这是一个处理弯曲时空的理论,该理论解释了(实际上是要求)宇宙黑洞的存在性。它表明,尽管光总是以同样的速度(一般用c来代表)运动,如米歇尔和拉普拉斯所设想尺度的物体,还是会捕捉住光,并且是黑暗的。
广义相对论发表后,成为一个多世纪以前冯·索德纳推测的回响。爱因斯坦的新理论预言,当星光经过太阳附近时光会发生偏转,但与牛顿理论中预期的偏转量有所不同。没有人曾经寻找过这种偏转,部分是因为当时虽然施行必要的检测已经成为可能,但人人都知道光是一种波,因而就不会受到冯·索德纳所建议方式的影响。但根据爱因斯坦的理论,波和粒子(或波粒二象性)都会被其行为(就像一个透镜的弯曲空间和太阳质量)所偏转。但你能在白天看到星星吗?测试这一预言的唯一方法就是等待日全食,那时就可能在太阳的方向上(但比太阳远得多)拍摄到星星。如果太阳弯曲空间使它像一个透镜那样的话,这些恒星视位置会稍微偏离。将这些照片与六个月后,当太阳处于地球另一侧,并且在夜晚能看见恒星时所拍摄的照片相比,就可以看出相同的恒星是否有所偏离。1919年有一次日食,偶然被拍下照片并加以对比,结果证明爱因斯坦理论是正确的(图1.3)。这个事件成为头条新闻,报道说牛顿的理论(并不完全彻底地)已经被推翻,爱因斯坦成为家喻户晓的名字。
光线弯曲的发现,引发了对于少数理论家怎么得到那些超前观念的少许迷惑,米歇尔和拉普拉斯那些被遗忘的揣测,不知不觉地又以更现代的方式发出了回响。现在,那些猜测第一次被加以认真的考虑,对于类似太阳这样的恒星,如果保持质量不变,但体积被挤压到一个更小的范围,使得从中心到表面的距离缩小,表面的引力增加时,它的逃逸速度将会发生什么样的情况呢?1920年,一名来自大学学院的研究人员高尔威(Galway)评论说:
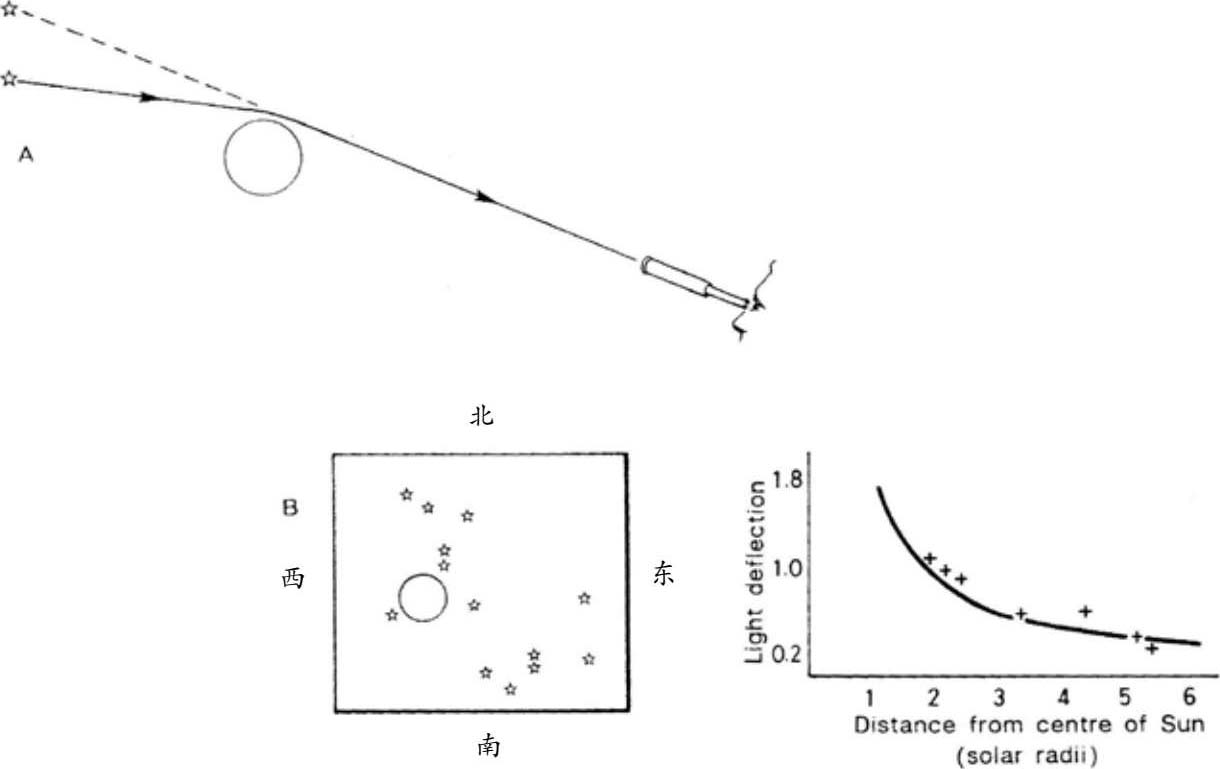
图1.3 A. 当遥远的星光靠近太阳附近时,“星光束”被太阳的引力所偏转。
B.在1919年的日食期间,由亚瑟·爱丁顿领导的一个观测小组测量了几个恒星的光的弯曲效应。不同的恒星星光有不同的偏转量(见图),完全符合爱因斯坦广义相对论的预测(实线)。
也许这个假设是很极端的,但我们还是应该说明一下。即,如果太阳的质量集中在一个直径1.47千米的球体内,那么接近它时的偏转率就是无限大。我们或许有了一个非常强大的聚光透镜,真正的强大,以至于太阳自身所发出的光在其表面也不会有速度了。如此一来,按照亥姆霍兹的建议,太阳的体积就会持续收缩,直到被黑暗所笼罩的那个时刻到来,并不是因为它没有光可发射,而是因为其引力场已经不透明了。
仅仅一年后,刚刚从伯明翰大学校长位置上退休的物理学家奥利弗·洛奇爵士(Sir Oliver Lodge)在同一杂志中写道:
一个质量足够大的高密度物体,将能留住光并防止它逃逸。其实体不需要是单一的质量或太阳,它应该是个有很多间隙的恒星系统……
洛奇意识到,我们现在所称的黑洞,如若其体积更大,则需要捕捉光线的物质密度就更低。原因是球体表面的引力强度不仅与到其中心的距离成平方反比(这使得质量相同但体积更大的球体引力减弱),而且也与球体内物质的数量有关。对于给定的密度,当其中心向外的距离增加时,体积也会增加。对于越来越大的给定密度区域,整体效果是,其表面的引力强度和逃逸速度都随着半径的增加而呈严格的线性增加。半径增加一倍,逃逸速度也会翻一倍。你可以把黑洞做成任何东西,具有任何你喜欢的密度,只要你能够让它填补一个足够大的区域范围。洛奇意识到,像我们银河系这样的恒星系统,含有成千上万亿的恒星,分布在半径为数千光年的区域内,就可能有一个大于光速的总逃逸速度,虽然系统内的恒星、行星和人类并没什么不寻常之处。我们可以不自觉地生活在一个黑洞之内。但他也意识到,如果原子可以被挤压在一起,如此紧密以至连原子核都彼此相接,也就有可能用不了一个太阳的质量,就能做成一个黑洞。
所有这些观念都超前了它们的时代大约半个世纪,而在20世纪20年代的时候它们都还没有出现。科学根本没准备好认真地接受暗星的概念——让暗星系寂寞孤独着。但与此同时,物理学家们更关心其他问题——整理出新的量子理论、利用爱因斯坦的质能关系来解释恒星是如何将热保持了那么久——黑洞的数学基础研究,例如,弯曲时空已经被攻克。的确,由卡尔·高斯、尼古拉·罗巴切夫斯基(Nikolai Lobachevsky)、亚诺什·鲍耶(János Bolyai)等,在19世纪上半叶已经奠定了基础。
在连接了从牛顿到爱因斯坦的全部科学历史链条,并涉足20世纪物理学的深水之后,现在是退后一点来观察这个19世纪的数学,和该世纪后半期由伯恩哈德·黎曼(Bernhard Riemann)充分发展了的非欧几里得几何思想是如何直接影响到爱因斯坦创建广义相对论的时候了。