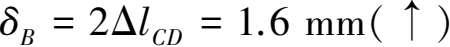【例题 2.1】 如图 2.1 所示的结构上作用荷载 F , AB 杆为钢杆,其横截面直径 d = 20 mm; BC 杆为木杆,其横截面为边长 a = 100 mm的正方形。已知 F = 20 kN,许用应力[ σ ] 钢 =160 MPa, [ σ ] 木 = 10 MPa,试对该结构进行强度校核。
【分析】 该题主要考查轴向拉压杆的强度计算。由于 AB 杆和 BC 杆的材料不同,其许用应力也不相同,故需要分别校核其强度。由题意可计算出两杆的横截面面积,只需要再计算出两杆的轴力,就可以通过正应力的计算公式进行强度校核。显然, AB 杆和 BC 杆均为二力杆,要计算各杆的轴力,可用截面法截取结点 B 附近的部分杆件进行受力分析,从而计算出相应的轴力。
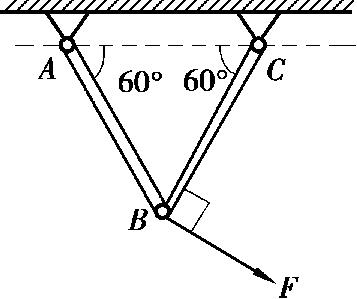
图 2.1 例题 2.1 图
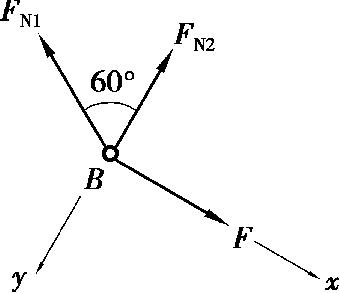
图 2.2
【解】 (1)计算各杆轴力。取结点 B 进行分析,建立坐标系,其受力图如图 2.2 所示。
由平衡方程
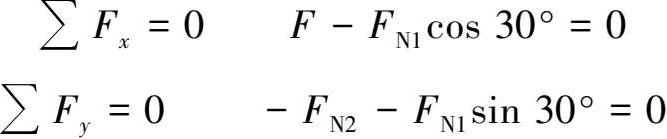
解得
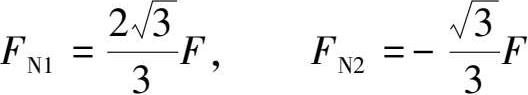
(2)校核钢杆的强度。
钢杆横截面上受到的正应力为:
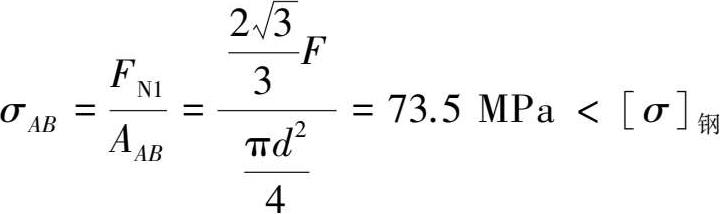
钢杆满足强度条件。
(3)校核木杆的强度。
木杆横截面上受到的正应力为:
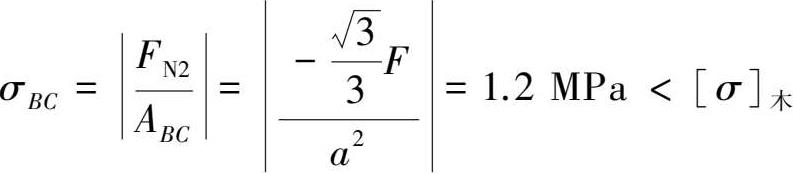
木杆满足强度条件。
综上,该结构满足强度条件。
【例题 2.2】 如图 2.3 所示, AB 是刚性杆,在 B 端受力偶 M e 作用,已知 CD 杆的截面积 A = 500 mm 2 , E = 200 GPa,[ σ ]= 160 MPa, l = 1 m。试求此结构所能承受的最大荷载 M e 以及此时 B 点的位移 δ B 。
【分析】 由于 AB 杆是刚性杆,不考虑其强度以及变形,仅考虑轴向拉压 CD 杆的强度、变形的计算,因此,对于题目要求计算的最大荷载 M e ,只需要根据 CD 杆满足强度条件就可以计算出来。对题目要求计算 B 点的位移 δ B ,除了要考虑 CD 杆的变形,还要考虑结构变形后的几何关系。
【解】 (1)计算 CD 杆的轴力。取 AB 杆为研究对象,其受力图如图 2.4 所示。
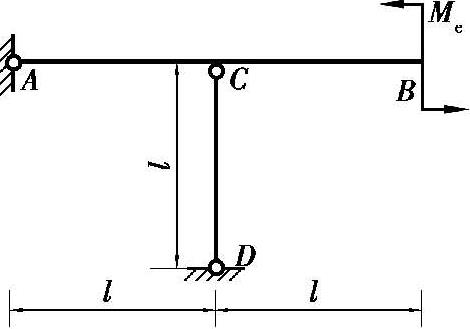
图 2.3 例题 2.2 图
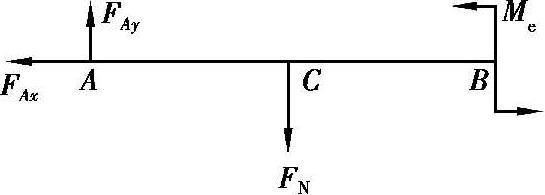
图 2.4
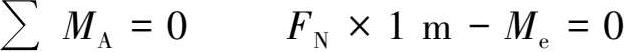
(2)确定最大荷载 M e 。
由强度条件
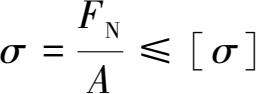
可得
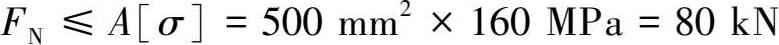
故
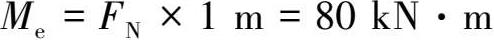
(3)计算 B 点的位移 δ B 。
CD杆的变形
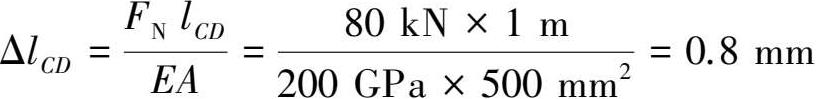
考虑变形后的几何关系,可知