下载掌阅APP，畅读海量书库
立即打开
我们已经知道一维树状数组修改和查询的时间复杂度均为 O (log n )，可以扩展为 m 维树状数组，其时间复杂度为 O (log m n)，对该算法只需加上一层循环即可。二维数组 a [ n ][ n ]、树状数组 c [][]的查询和修改方法如下。
（1）查询前缀和。二维数组的前缀和实际上是从数组左上角到当前位置( x , y )矩阵的区间和，在一维数组查询前缀和的代码中加上一层循环即可。
算法代码：
（2）更新。若对 a [ x ][ y ]进行修改（加上 z ），则在一维数组更新的代码中加上一层循环即可。
算法代码：
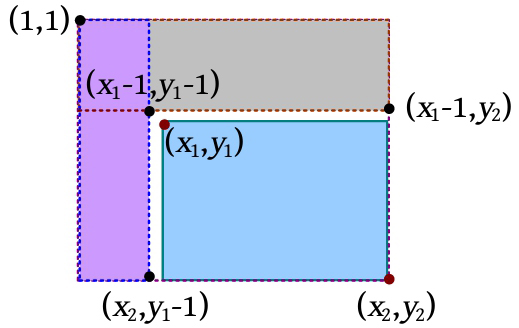
（3）查询区间和值。对二维数组查询区间和，实际上是求从左上角( x 1 , y 1 )到右下角( x 2 , y 2 )子矩阵的区间和。先求出左上角(1, 1)到右下角( x 2 , y 2 )的区间和sum( x 2 , y 2 )，然后减去(1, 1)到( x 1 -1, y 2 )的区间和sum( x 1 -1, y 2 )，再减去(1, 1)到( x 2 , y 1 -1)的区间和sum( x 2 , y 1 -1)，因为这两个矩阵的交叉区域多减了一次，所以再加回来，加上(1, 1)到( x 1 -1, y 1 -1)的区间和sum( x 1 -1, y 1 -1)。
算法代码：
树状数组主要用于查询前缀和、区间和及点更新，对点查询、区间修改效率较低。
前缀和查询： 求 a [1].. a [ i ]的前缀和，普通数组需要 O ( n )时间，树状数组需要 O (log n )时间。
区间和查询： 求 a [ i ].. a [ j ]的区间和，普通数组需要 O ( n )时间，树状数组需要 O (log n )时间。
点更新： 修改 a [ i ]加上 z ，普通数组需要 O (1)时间，树状数组需要 O (log n )时间。
点查询： 查找第 i 个元素，普通数组需要 O (1)时间，树状数组需要 O (log n )时间（求sum[ i ]-sum[ i -1]）。
区间修改： 若对一个区间 a [ i ].. a [ j ]的所有元素都加上 z ，则普通数组需要 O ( n )时间，树状数组不能有效操作，只能一个一个地修改和更新，需要 O ( n log n )时间。
减法规则： 当问题满足减法规则时，例如求区间和 a [ i ].. a [ j ]，则sum( i , j )=sum[ j ]-sum[ i -1]。当问题不满足减法规则时，例如求区间 a [ i ].. a [ j ]的最大值，则不可以用 a [1].. a [ j ]的最大值减去 a [1].. a [ i -1]的最大值，此时可以用线段树解决。