题目描述(HDU2586): 有 n 栋房屋,由一些双向道路连接起来。每两栋房屋之间都有一条独特的简单道路(“简单”意味着不可以通过两条道路去一个地方)。人们每天总是喜欢这样问:“我从A房屋到B房屋需要走多远?”
输入: 第1行是单个整数 T ( T ≤10),表示测试用例的数量。每个测试用例的第1行都包含 n (2≤ n ≤40000)和 m (1≤ m ≤200),表示房屋数量和查询数量。下面的 n -1行,每行都包含三个数字 i、j、k ,表示有一条道路连接房屋 i 和房屋 j ,长度为 k (0< k ≤40000),房屋被标记为1~ n 。接下来的 m 行,每行都包含两个不同的整数 i 和 j ,求房屋 i 和房屋 j 之间的距离。
输出: 对每个测试用例,都输出 m 行查询答案,在每个测试用例后都输出一个空行。

题解: 本题中任意两个房子之间的路径都是唯一的,是连通无环图,属于树形结构,所以求两个房子之间的距离相当于求树中两个节点之间的距离。可以采用最近公共祖先LCA的方法求解。求解LCA的方法有很多,在此使用树上倍增+ST解决。
(1)根据输入数据采用链式前向星存储图。
(2)深度优先搜索,求深度、距离,初始化F[ v ][0]。
(3)创建ST。
(4)查询 x 、 y 的最近公共祖先lca 。
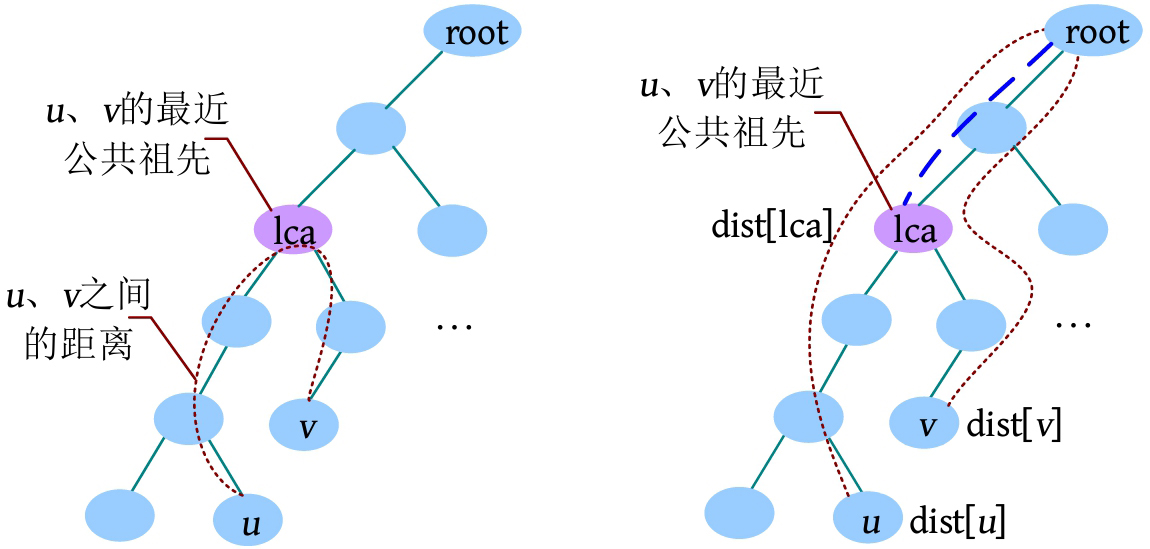
(5)输出 x、y 的距离dist[ x ]+dist[ y ]-2×dist[lca]。
求 u 和 v 之间的距离,若 u 和 v 的最近公共祖先为lca,则 u 和 v 之间的距离为 u 到树根的距离加上 v 到树根的距离,再减去2倍的lca到树根的距离:dist[ u ]+dist[ v ]-2×dist[lca]。