树上倍增法不仅可以解决LCA问题，还可以解决很多其他问题，掌握树上倍增法是很有必要的。

F[ i , j ]表示 i 的2 j 辈祖先，即 i 节点向根节点走2 j 步到达的节点。

u 节点向上走2 0 步，则为 u 的父节点 x ，F[ u , 0]= x ；向上走2 1 步，到达 y ，F[ u , 1]= y ；向上走2 2 步，到达 z ，F[ u , 2]= z ；向上走2 3 步，节点不存在，令F[ u , 3]=0。

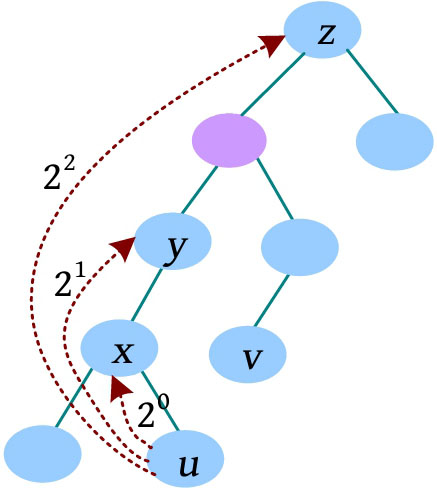
F[ i , j ]表示 i 的2 j 辈祖先，即 i 节点向根节点走2 j 步到达的节点。可以分两个步骤： i 节点先向根节点走2 j -1 步得到F[ i , j -1]；再从F[ i , j -1]节点出发向根节点走2 j -1 步，得到F[F[ i , j -1], j -1]，该节点为F[ i , j ]。

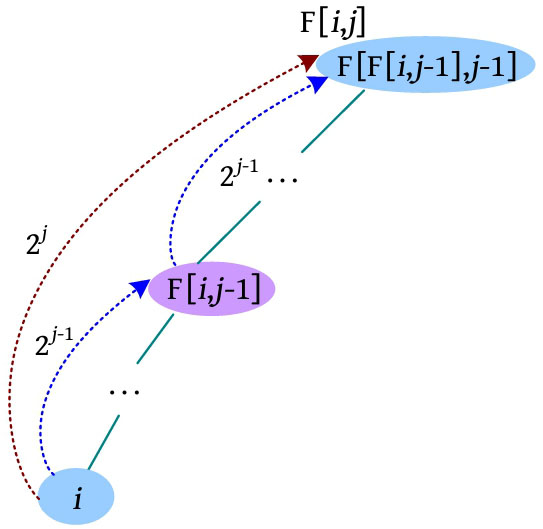
递推公式：F[ i , j ]=F[F[ i , j -1], j -1]， i =1, 2, … n ， j =0, 1, 2, … k ，2 k ≤ n ， k =log 2 n 。

1. 算法设计

（1）创建ST。

（2）利用ST求解LCA。

2. 完美图解

和前面暴力搜索中的同步前进法一样，先让深度大的节点 y 向上走到与 x 同一深度，然后 x、y 一起向上走。和暴力搜索不同的是，向上走是按照倍增思想走的，不是一步一步向上走的，因此速度较快。

问题一： 怎么让深度大的节点 y 向上走到与 x 同一深度呢？

假设 y 的深度比 x 的深度大，需要 y 向上走到与 x 同一深度， k =3，则求解过程如下。

（1） y 向上走2 3 步，到达的节点深度比 x 的深度小，什么也不做。

（2）减少增量， y 向上走2 2 步，此时到达的节点深度比 x 的深度大， y 上移， y =F[ y ][2]。

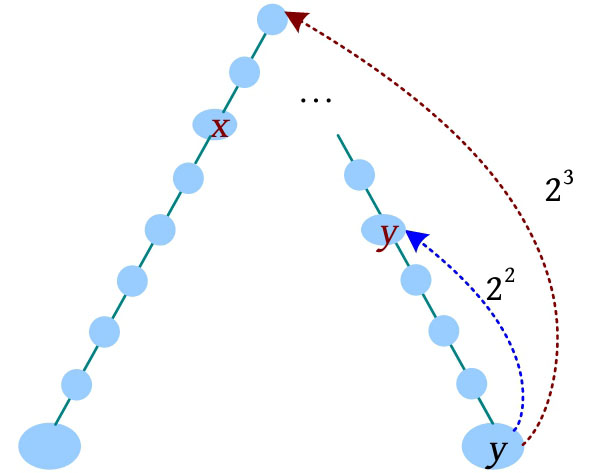
（3）减少增量， y 向上走2 1 步，此时到达的节点深度与 x 的深度相等， y 上移， y =F[ y ][1]。

（4）减少增量， y 向上走2 0 步，到达的节点深度比 x 的深度小，什么也不做。此时 x、y 在同一深度。

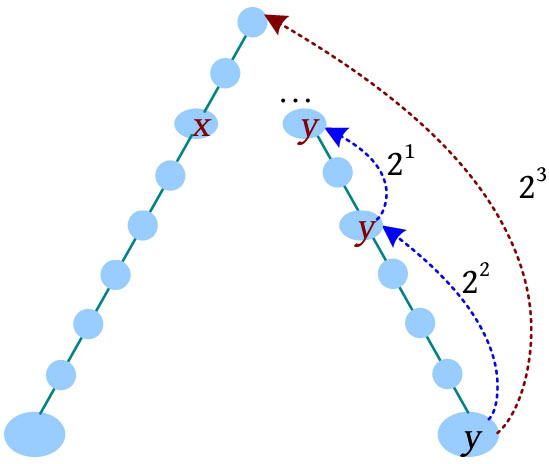
总结：按照增量递减的方式，到达的节点深度比 x 的深度小时，什么也不做；到达的节点深度大于或等于 x 的深度时， y 上移，直到增量为0，此时 x、y 在同一深度。

问题二： x、y 一起向上走，怎么找最近的公共祖先呢？

假设 x 、 y 已到达同一深度，现在一起向上走， k =3，则其求解过程如下。

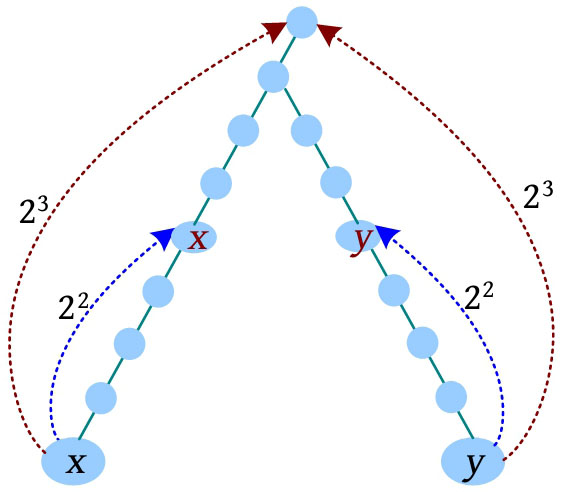
（1） x 、 y 同时向上走2 3 步，到达的节点相同，什么也不做。

（2）减少增量， x 、 y 同时向上走2 2 步，此时到达的节点不同， x 、 y 上移， x =F[ x ][2]， y =F[ y ][2]。

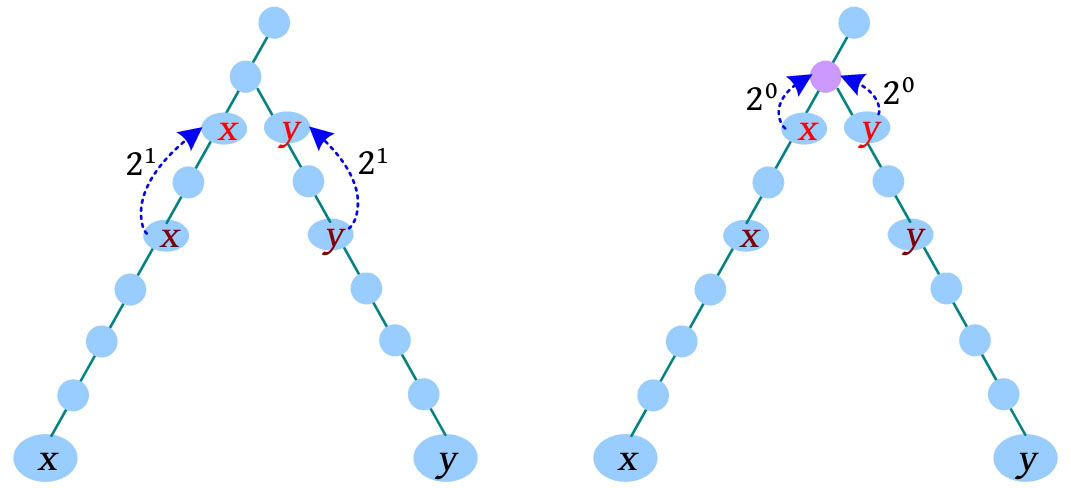
（3）减少增量， x 、 y 同时向上走2 1 步，此时到达的节点不同， x 、 y 上移， x =F[ x ][1]， y =F[ y ][1]。

（4）减少增量， x 、 y 同时向上走2 0 步，此时到达的节点相同，什么也不做。

此时 x 、 y 的父节点为最近公共祖先节点，即LCA( x , y )=F[ x ][0]。

完整的求解过程如下图所示。

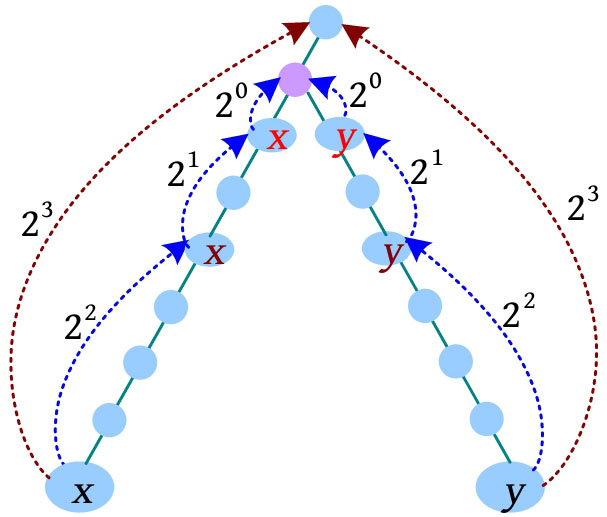
总结：按照增量递减的方式，到达的节点相同时，什么也不做；到达的节点不同时，同时上移，直到增量为0。此时 x 、 y 的父节点为公共祖先节点。

3. 算法实现

4. 算法分析

采用树上倍增法求解LCA，创建ST需要 O ( n log n )时间，每次查询都需要 O (log n )时间。一次建表、多次使用，该算法是基于倍增思想的动态规划，适用于多次查询的情况。若只有几次查询，则预处理需要 O ( n log n )时间，还不如暴力搜索快。 irr+DaPNphC7terzKAO7z83U3Dke6OebNFrK6mVuKA0aBUUY2HJKun/UbEhbGvvc