ST（Sparse Table，稀疏表）算法采用了倍增思想，在 O ( n log n )时间构造一个二维表之后，可以在 O (1)时间在线查询[ l , r ]区间的最值，有效解决在线RMQ（Range Minimum/Maximum Query，区间最值查询）问题。

如何实现呢？设F[ i , j ]表示[ i , i +2 j -1]区间的最值，区间长度为2 j 。

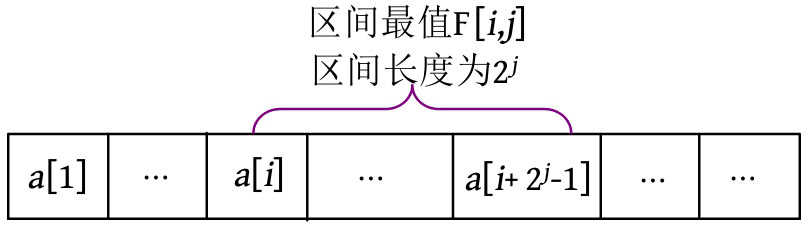
根据倍增思想，长度为2 j 的区间可被分成两个长度为2 j -1 的子区间，然后求两个子区间的最值即可。递推公式：F[ i , j ]=max(F[ i , j -1], F[ i +2 j-1 , j -1])。

1. ST创建

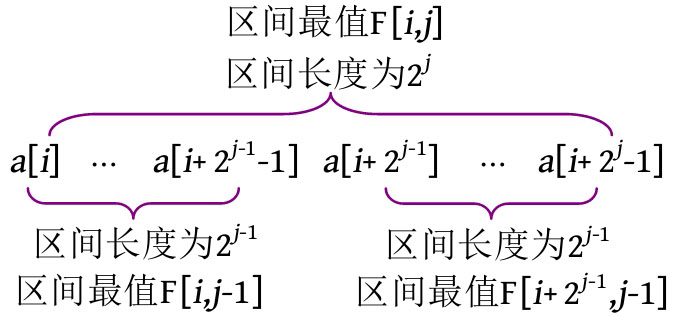
若F[ i , j ]表示[ i , i +2 j -1]区间的最值，区间长度为2 j ，则 i 和 j 的取值范围是多少呢？

若数组的长度为 n ，最大区间长度2 k ≤ n <2 k +1 ，则 k = 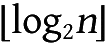，比如 n =8时 k =3， n =10时 k =3。在程序中， k =log2( n )，也可用通用表达方式 k =log( n )/log(2)，log()表示以e为底的自然对数。

算法代码：

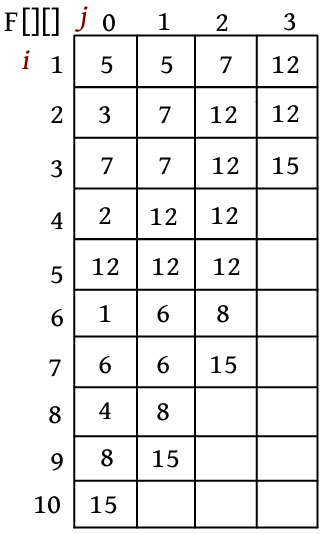
例如有10个元素 a [1..10]={5, 3, 7, 2, 12, 1, 6, 4, 8, 15}，其查询最值的ST如下图所示。

F[ i , j ]表示[ i , i +2 j -1]区间的最值，区间长度为2 j 。

· F[1, 0]表示[1, 1+2 0 -1]区间，即[1, 1]的最值为5，第0列为数组自身。

· F[1, 1]表示[1, 1+2 1 -1]区间，即[1, 2]的最值为5。

· F[2, 3]表示[2, 2+2 3 -1]区间，即[2, 9]的最值为12。

· F[6, 2]表示[6, 6+2 2 -1]区间，即[6, 9]的最值为8。

2. ST查询

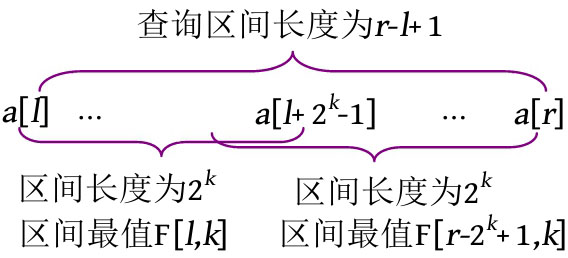
若查询[ l , r ]区间的最值，则首先计算 k 值，和前面的计算方法相同，区间长度为 r - l +1，2 k ≤ r - l +1<2 k +1 ，因此 k =log2( r - l +1)。

若查询区间的长度大于或等于2 k 且小于2 k +1 ，则根据倍增思想，可以将查询区间分为两个查询区间，取两个区间的最值即可。两个区间分别为从 l 向后的2 k 个数及从 r 向前的2 k 个数，这两个区间可能有重叠，但对求最值没有影响。

算法代码：

3. 算法分析

创建ST时，初始化需要 O ( n )时间，两个 for 循环需要 O ( n log n )时间，总时间复杂度为 O ( n log n )。区间查询实际上是查表的过程，计算 k 值后从表中读取两个数取最大值即可，因此查询的时间复杂度为 O (1)。一次建表，多次使用，这种查表法就是动态规划。 yxYqHHtXk9GCNLhIubvBoEI/H3g3Vy2eJ8DJ6SMO0R0ydZQ098upVQEdV1U5b0+S