在零假设显著性检验（null hypothesis significance testing，NHST）中，第一类错误率α称作显著性水平（level of significance），是事先确定的、错误地拒绝零假设所承担的风险。Significant一词的常见意思是“有意义的”（meaningful）和“重要的”（important），但是在统计学中，significant指“显著（性）的”或“有显著意义的”，意为“可能为真”或“非随机的”。在前面讨论置信区间时，我们已经注意到，随着样本的变化，样本平均数以及总体平均数置信区间也随之变化。虽然我们不能准确知道总体参数值，但是在一定的置信水平上能够估计总体参数值的范围。譬如，如果在95％的置信水平上由样本推断的置信区间包括 μ 0，则我们有理由不拒绝零假设，否则拒绝零假设。因此，置信区间与统计显著性检验是紧密联系的。或者说，置信区间是统计检验的一种方式。本节主要讨论统计显著性检验使用的临界值和概率 p （probability的缩写）值。

概率 p 值是条件概率，表示在零假设为真的情况下，得到本研究之值或更极端之值的概率，即显著性概率（significance probability）。统计量（statistic）的显著性表明对某个差异或关系的把握性程度。显著性差异可大可小，显著性关系可强可弱。在研究报告中， α 和 p 通常是联系在一起的。假定 α ＝0.05， p ＝0.04（概率值前面的“0”可以省略，如 α ＝.05， p ＝.04），常用的标准表述形式是：在 α ＝0.05的显著性水平上，零假设被拒绝，或是 p ＝0.04＜0.05。小于0.05的 p 值表明，零假设为真时，某个结果或更极端结果偶然发生的可能性不到5％，由此推断该结果有显著意义（significant）。如果 p 值大于0.05，我们通常认为研究结果没有显著性意义，即没有足够的证据拒绝零假设。在实际研究中，α选择0.05、0.01还是0.001取决于研究者对第一类错误严重性的认识。通常情况下，我们选择 α ＝0.05。

这里以单样本 t 检验为例说明统计显著性检验的基本逻辑。假如有一个正态分布的总体，平均数 μ ₀ ＝20，方差 σ ² 未知。我们从某一个正态分布总体中随机抽取 n ＝20的样本，它的平均数 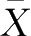＝23，标准差 s ＝4.5。试检验该样本所在的总体是否为 μ ₀ ＝20的正态分布总体。本例的零假设是 μ ＝ μ ₀ ＝20，研究假设是 H 1： μ ≠ μ ₀ ，统计检验采用双侧检验。

在样本来自正态分布、总体标准差（或方差）未知的情况下检验该样本是否来自某个总体采用单一样本 t 检验，即检验某样本平均数 与一个总体平均数 μ ₀ 之间是否存在显著性差异。通常，如果 p ＜0.05，拒绝零假设，有可靠证据表明样本来自平均数为 μ 的另外一个总体。如果 p ＞0.05，不拒绝零假设，没有可靠证据表明样本不是来自平均数为 μ 0 的总体。针对上面的例子，根据单一样本 t 检验统计量计算公式 t ＝ ，得到 t ＝2.98。在零假设为真的条件下，检验统计量 t 服从自由度 ν ＝19的 t 分布。当 α ／2＝0.025时，右尾 t 临界值为2.09（R命令为qt（0.975，19））。由于 t 分布是对称分布，左尾 t 临界值为－2.09，如图4.6所示。

图4.6显示两大区域，一个是非拒绝区（non－rejection region），另一个是拒绝区（rejection region）。非拒绝区为1－ α ＝95％置信区间。零假设为真的条件下，在95％置信水平上样本统计量 t 值介于±2.09之间。在±2.09区间之外的区间为拒绝区，为样本统计量 t 值落入的区域。本例采用双侧检验，在下尾巴和上尾巴各有一个拒绝区。如果采用单侧检验，则只有一个拒绝区。在零假设为真和置信水平为0.95的条件下，拒绝区是样本统计量 t 值不太可能落入的范围。本例中，如果样本统计量 t 值落入拒绝区，说明样本数据来自的总体分布不太可能是 μ ₀ ＝20的正态分布，由此拒绝零假设。本例的样本统计量 t 值为2.98，落入 t 分布上尾巴的拒绝区，因而拒绝零假设，即推断样本所在的总体不是 μ ₀ ＝20的正态分布总体。

思考与练习

1.举例说明95％置信区间的含义。

2.简要解释统计显著性概念。

3.某研究者推测50％以上的大学生会对当前的大学英语教学模式感到满意，于是开展了一项满意度调查，检验自己的推测。这项调查研究的零假设（ H 0）和备择假设（ H a ）是下面的哪个选项？

（a） H ₀ ： p ＝0.5； H _a ： p ≠0.5

（b） H ₀ ： p ＝0.5； H _a ： p ＞0.5

（c） H ₀ ： p ＞0.5； H _a ： p ≠0.5

（d） H ₀ ： p ＞0.5； H _a ： p ＝0.5

4.某大学调整大学英语课程设置，旨在提高学生对课程设置的认可度。在课程设置调整前，70％的大学生认可英语课程的设置。课程设置调整后，教务部门从3 000名大学生中随机抽取200名学生开展了调查，发现150名学生认可新的课程设置方式。适合于本次调查的推理统计方法是单样本 Z 检验。统计量 Z 服从标准正态分布，计算公式为： Z ＝ ，其中 是样本中结果发生的比率（proportion）， p _{0 是} 零假设条件下总体（population）中结果发生的比率， n 是样本量。对本例开展单样本 Z 检验，得到 Z ＝1.543， p ＝0.061。回答以下问题：

（a）本研究的零假设和备择假设是什么？

（b）调查中认可新版英语课程设置的学生比率是多少？

（c）设定统计显著性水平 α ＝0.05，本研究得出的结论是什么？

（d）本研究中的第一类错误和第二类错误是什么？

（e）本研究发现认可新版英语课程设置的学生比率 p ＝0.75 的统计效力只有0.476。这是什么意思？

（f）你对提高统计效力的建议是什么？

5.一项研究报告在统计显著性水平 α ＝0.05 时，某个统计检验的统计效力为0.82。试问：该检验的第一类错误率和第二类错误率各是多少？

6.某研究者对随机抽取的50名大学生开展了英语水平测试，测试分数（Scores）如下：68，61，57，52，70，68，71，75，65，81，74，74，55，65，73，76，67，77，75，81，84，78，75，64，65，75，69，58，66，78，63，77，82，73，77，60，60，68，68，60，57，60，72，68，71，72，70，63，61，25。给出计算（算术）平均数和20％截尾平均数的R命令，报告统计结果。

7.给出计算第6题中英语水平测试分数的标准差和20％缩尾标准差的R命令，报告统计结果。这两个标准差差异大吗？为什么？

8.利用R函数shapiro.test对第6题中英语水平测试分数开展正态性检验，报告检验结果。如果删除第6题中的英语水平测试分值25，对其他分数开展正态性检验，检验的结论发生改变了吗？如果检验的结论发生改变，这说明什么？

9.利用第6题中英语水平测试分数，计算总体（算术）平均数的95％置信区间和总体20％截尾平均数的95％置信区间。给出计算置信区间的R命令，报告统计结果。针对本例，你更愿意接受总体平均数的95％的置信区间，还是总体20％截尾平均数的95％置信区间？请给出理由。

10.显著性概率 p 与第一类错误率 α 有何区别？

11.第一类错误和第二类错误相比，哪类错误更直接地被零假设显著性检验所控制？

12.总体平均数95％置信区间表示我们有95％的信心或把握认为真正的总体平均数位于这个区间。有一位研究者发现总体平均数的一个 95％置信区间为［25.5，32.3］，认为这个区间包括真正总体平均数的概率为95％。为什么这种认识是错误的？

13.在所有的总体平均数95％置信区间中，有多少比率的置信区间包括样本平均数？

（a）大约有95％

（b）100％

（c）大约有5％

（d）依研究使用的样本量而定

14.下面哪个关于总体比率 p 的95％置信区间会使我们拒绝零假设 H ₀ ： p ＝0.6，接受备择假设 H _a ： p ≠0.6？

（a）［0.65，0.75］

（b）［0.47，0.60］

（c）［0.55，0.62］

（d）［0.57，0.70］

15.从正态分布总体中随机抽取样本量为25的一个样本（ n ＝25）。已知样本平均数为 ＝60，标准差为 s ＝10，编写R命令计算在第一类错误率 α ＝0.05时总体平均数95％置信区间（保留两位小数）。

16.样本量为30时计算总体平均数99％置信区间所需的临界值 t 是多少（保留两位小数）？要求给出R命令。 rF+ywG7WwJsitS0Ivl2dCCnO8T1c49cvfzliubD8A8US36mUQ2WL0PTEijSz1+5x