





有时候,平均数和中位数作为位置估计都不很理想。一种解决方法是采用稳健(robust)的位置测量——截尾平均数(trimmed mean,
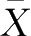 t
)。稳健性指统计分析方法对统计假设少量偏离的不敏感性(Huber,1981,p.2)。截尾量称作
γ
。20%是最常用的
γ
值。20%截尾平均数是最常用的稳健统计量,在大多数情况下表现优良。中位数是截尾平均数的特例,因为截尾量大约为50%。
t
)。稳健性指统计分析方法对统计假设少量偏离的不敏感性(Huber,1981,p.2)。截尾量称作
γ
。20%是最常用的
γ
值。20%截尾平均数是最常用的稳健统计量,在大多数情况下表现优良。中位数是截尾平均数的特例,因为截尾量大约为50%。
截尾平均数在预先确定截尾量之后对样本截尾平均数进行计算。将一组数据由小到大排序,然后从两端截除样本20%的数值,由此得到剩余数值的平均数即为20%截尾平均数。令 g =[0.2 n ],即 g 取0.2 n 的整数部分,则20%截尾平均数的计算公式为:

假如有变量
X
的一组数值(
n
=32):56,61,54,49,64,66,48,52,68,62,67,61,57,58,61,52,62,65,59,60,63,50,71,69,55,56,58,51,56,73,100,150,试求20%截尾平均数。首先,将该组数据由小到大排序,得到:48,49,50,51,52,52,54,55,56,56,56,57,58,58,59,60,61,61,61,62,62,63,64,65,66,67,68,69,71,73,100,150。由于
g
=[0.2
n
]=6,20%截尾后的值为:54,55,56,56,56,57,58,58,59,60,61,61,61,62,62,63,64,65,66,67。根据公式3.4,得到
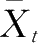 =60.05。R计算截尾平均数的函数为来自数据包Rallfun-v37中的函数tmean(x,tr=0.2),其中x是数值向量,tr表示截尾量,函数默认值为0.2,即计算20%截尾平均数。如果设置tr=0,则函数tmean计算常规的平均数;如果设置tr=0.5,则函数tmean计算中位数。本例数据的平均数
=60.05。R计算截尾平均数的函数为来自数据包Rallfun-v37中的函数tmean(x,tr=0.2),其中x是数值向量,tr表示截尾量,函数默认值为0.2,即计算20%截尾平均数。如果设置tr=0,则函数tmean计算常规的平均数;如果设置tr=0.5,则函数tmean计算中位数。本例数据的平均数
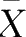 =63.56,中位数
Mdn
=60.5。由于本例有两个异常值(100和150),截尾平均数
=63.56,中位数
Mdn
=60.5。由于本例有两个异常值(100和150),截尾平均数
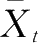 与中位数
Mdn
接近,但是与平均数
与中位数
Mdn
接近,但是与平均数
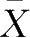 差异较大。
差异较大。