电阻器(简称“电阻”)可以说是电子电路中应用最广泛的基础元件。我们知道,在电阻两端施加一定的电压 V 后,电阻中就会流过一定的电流 I 。那么, V 与 I 之间又存在什么关系呢?我们通过实验,把不同的电压与对应的电流记录下来,这样就可以在平面直角坐标系(电压为横坐标,电流为纵坐标)中绘出电阻的 V - I 关系曲线,也称其为伏安特性曲线( V - I Characteristics Curve),如图2.1所示。
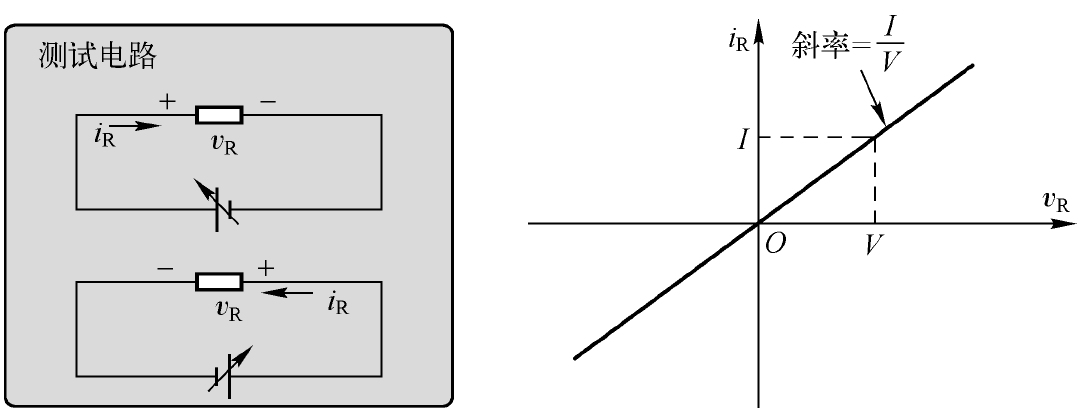
图2.1 电阻的伏安特性曲线
很明显,电阻的伏安特性曲线是一条直线。所以,流过电阻的电流与其两端施加的电压是呈正比的,这就是电阻的导电特性。我们把曲线上任意一点的电压与电流的比值定义为电阻的阻值 R (直线斜率的倒数),则有著名的欧姆定律(Ohm’s Law)表达式:

电阻的具体应用有很多, 限制回路的电流 (简称“限流”)就是其中之一。假设图2.1所示电路中的测试电压为1V,要求设置回路的电流为1mA,我们就可以根据欧姆定律计算出电阻的阻值应为1V/1mA=1kΩ。反过来,如果已知测试电压为1V,而电阻的阻值为1kΩ,也可以分析出回路的电流应为1mA。换句话说,我们通过观察电阻的伏安特性曲线总结出相应的导电特性后,就可以在电子电路分析与设计中合理地使用它了。
同样的道理,为了能够合理地使用PN结,我们需要先了解其相应的导电特性。与获得电阻的导电特性的方式一样,我们可以在PN结两端施加一定的电压并观察流过的电流,如图2.2所示。
从图2.2中可以看到,外接电压 V F 的正极接P区,而负极接N区,我们称这种连接方式为正向偏置(Forward Bias),相应的外接电压 V F 可以称为正向偏置电压(可简称为“正向偏压”或“正偏电压”)。“偏置”是电子技术中的行业术语,大家初次接触可能会有些陌生,它是一种利用直流电压为电路设置固定直流电流与电压的广义称谓,可以理解为“施加电压”的意思,它使某个节点偏离原来的电位。简单地说,就是设置电路的直流电位,相关的术语还有偏置电流、偏置电阻和偏置电路等。
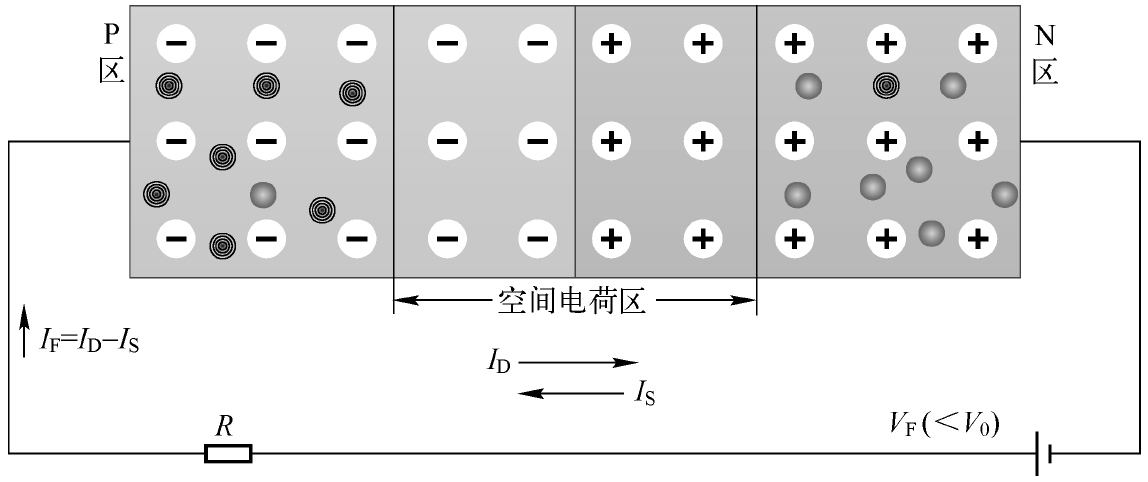
图2.2 施加较小的正向电压
由于 V F 产生的外电场方向与PN结的内电场方向是相反的,所以外电场起到削弱内电场的作用。此时,PN结的平衡状态被破坏,P区的多子(空穴)与N区的多子(电子)都会向PN结迁移,前者会与一部分负离子中和,使P区的空间电荷量减少,后者会与一部分正离子中和,使N区的空间电荷量减少。也就是说,此时的空间电荷区会变得更窄一些,扩散作用力会稍大于漂移作用力。但是,我们前面提到过内建电位差 V 0 ,如果 V F < V 0 ,虽然空间电荷区变窄了,但势垒区仍然还是存在的,所以PN结所呈现的电阻率仍然比较高,此时其就相当于一个大电阻。
如果把由于扩散作用力而形成的电流标记为 I D ,把由于漂移作用力而形成的电流标记为 I S ,那么此时的回路电流 I F (Forward Current)就是两者之差( I D - I S ),我们也可以称 I F 为“正向偏置电流”。当 V F < V 0 时, I D 会稍大于 I S ,所以 I F 还是比较小的,也就相当于回路是不导通的。
当 V F > V 0 时,空间电荷区会进一步变窄,这样势垒也就越小了,此时的扩散作用力远大于漂移作用力,P区与N区中能越过势垒的多子会大大增加而形成扩散电流,相当于被两个电阻率比较低的杂质半导体连通了,此时回路的正向电流 I F 是比较大的,如图2.3所示。
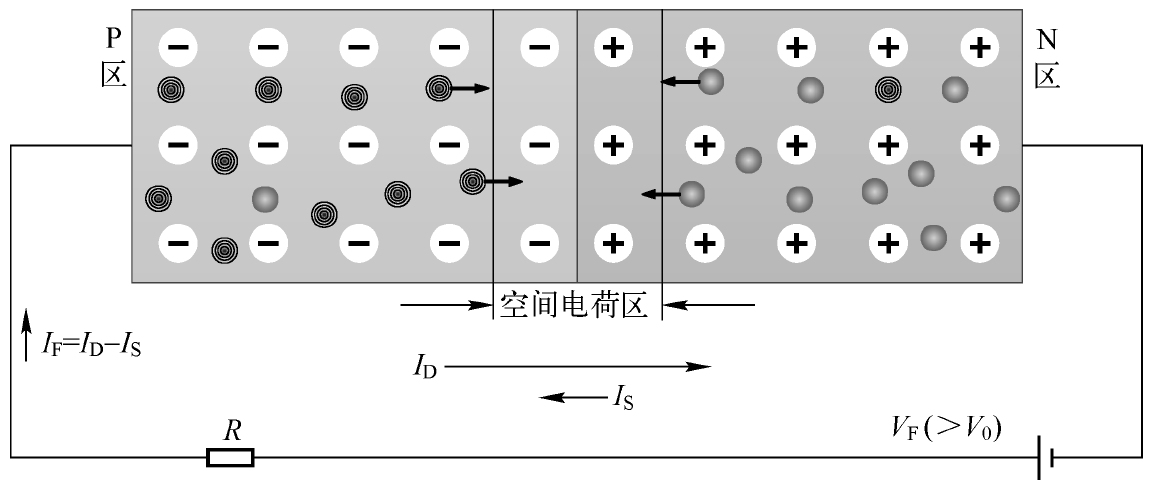
图2.3 施加较大的正向电压
很明显,正向电流 I F 主要是由多子的扩散运动而形成的。由于少子形成的漂移电流很小,可以忽略不计。
接下来我们给PN结施加反向偏置电压 V R 。如图2.4所示,由于此时外电场的方向与内电场的方向是一致的,所以空间电荷区会被进一步拓宽。从势垒的角度来看,多子要通过空间电荷区就更难了,所以扩散电流 I D 几乎为零。回路中存在的反向偏置电流主要由漂移电流 I S 形成,我们使用符号 I R 来表示(Reverse Current),它也可以表达为 I D 与 I S 的差值。很明显, I R 主要是由少子的漂移运动而形成的。由于少子本身的数量很少,所以产生的电流也比较小。
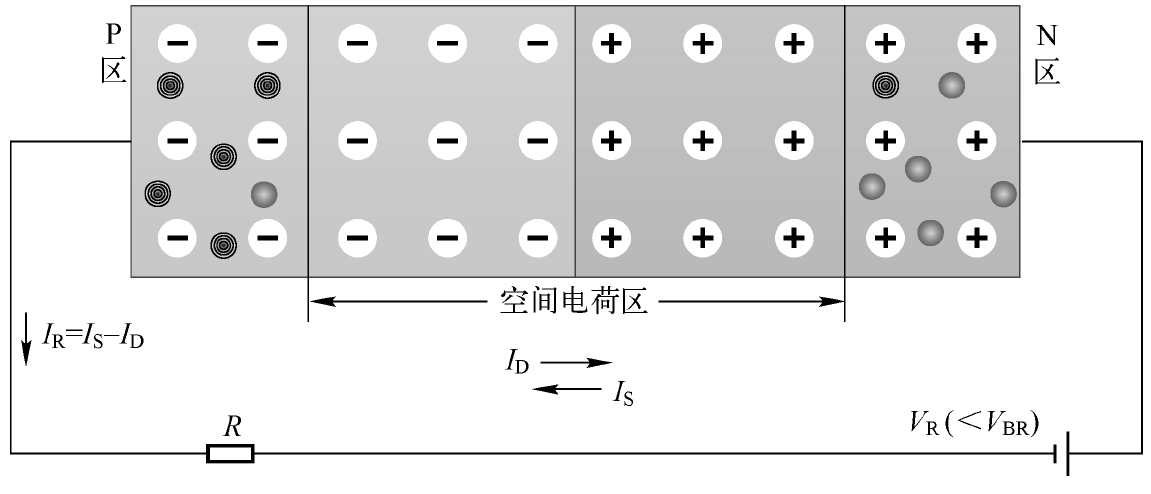
图2.4 施加较小的反向电压
当 V R 进一步被提升时,虽然空间电荷区理论上会越来越宽、 I R 会越来越小,但是当 V R 上升到一定程度时, I R 会突然急剧增加,我们把这种现象称为反向击穿,把发生反向击穿现象所需要的偏置电压称为反向击穿电压(Breakdown Voltage),使用符号 V BR 来表示。
有人可能会想了:既然反向电场会使空间电荷区进一步变宽,那么阻挡多子扩散的能力就会越强,为什么一下子就好像导通了呢?实际上,当外加的反向电场很强的时候,虽然空间电荷区会变宽,但是仍然存在两种情况,可能会导致空间电荷区的载流子数目急剧增加,从而引起 I R 的急剧上升,继而呈现反向击穿的现象。
第一种是雪崩效应(Avalanche Effect),它通常发生在掺杂浓度比较低的PN结当中。由于半导体的掺杂浓度比较低,为了最终获得与多子扩散作用力达到平衡的漂移作用力,空间电荷区需要进一步拓宽而容纳更多的正负离子,因此这种PN结的空间电荷区是比较宽的,如图2.5所示。
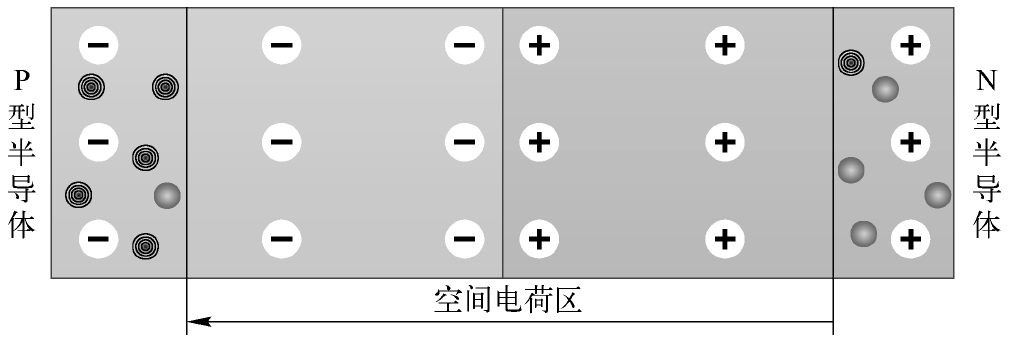
图2.5 掺杂浓度低的PN结
当这种PN结施加的反向偏压持续增大时,空间电荷区还会被进一步拓宽,在外电场的作用下,少子的漂移速度就会相应加快(载流子的动能增大)。由于空间电荷区是很宽的,所以少子在这个区域有一段比较长的路程要跑,而少子在跑的过程中就会被进一步加速,电子运动的速度就会越来越快,正如一直在以恒定加速度行驶的汽车一样,路程越长,加速时间也就越长,最后汽车的速度也就越快。
载流子在运动的过程当中总是会不断地与晶格原子或杂质离子进行碰撞,这些高速运动的载流子获得足够的动能就可以把束缚在共价键中的价电子碰撞出来而产生新的电子空穴对,而新产生的载流子也同样高速地碰撞其他晶格原子或杂质离子,又产生新的电子空穴对,由此产生的连锁反应将使得空间电荷区的载流子数量急剧增多,最后回路中的反向电流也就急剧增大了,如同发生雪崩一样。
第二种是齐纳效应(Zener Effect),它通常发生在掺杂浓度比较高的PN结当中。由于半导体的掺杂浓度比较高,为了最终获得与载流子扩散作用力达到平衡的漂移作用力,只需要很窄的空间电荷区就可以产生足够的内电场,因此这种PN结的空间电荷区是比较窄的,如图2.6所示。
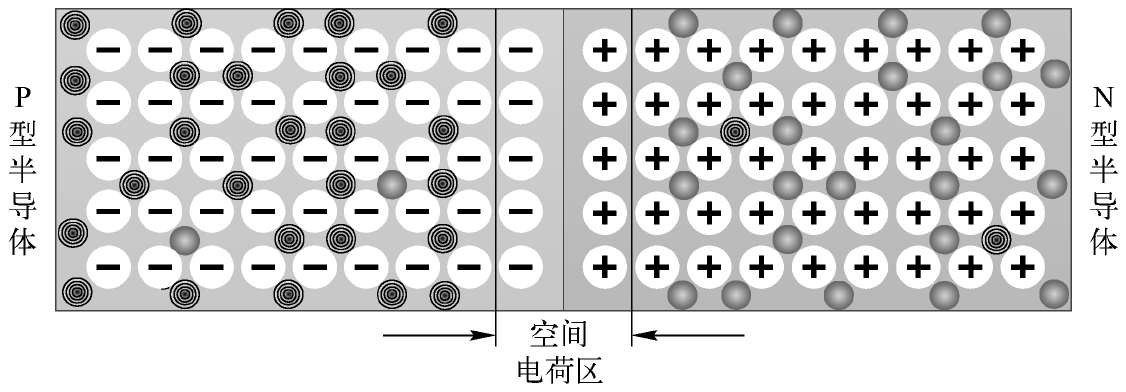
图2.6 掺杂浓度高的PN结
掺杂浓度影响空间电荷区宽度的原理,与战争中攻击敌方的堡垒有异曲同工之妙。我们的攻击力就相当于载流子的扩散作用力,而堡垒的防守力就相当于内电场对载流子的漂移作用力。掺杂浓度低相当于敌方的堡垒越稀疏,我们就可以拿下更多的疆土,空间电荷区也就会更宽,由于兵力总是有限的,所以最终会达到一个平衡状态。相反,掺杂浓度越高就相当于敌方的堡垒越密集,只要我们攻下距离很短的堡垒就会感到压力非常大,那么相同的兵力就只能拿下更少的疆土,空间电荷区也就会更窄。
我们同样与以恒定加速度行驶的汽车来做比较,只不过因为空间电荷区比较窄,路程也比较短,所以最后载流子的速度也并不快。也就是说,载流子与晶格原子或杂质离子发生碰撞的机会比较少。然而,正因为空间电荷区比较窄,只要给PN结施加不大的反向电压,就能够建立很强的电场,这足以把空间电荷区中晶格原子的价电子直接从共价键中拉出来(破坏共价键结构),从而产生电子与空穴对,我们称为场致激发,这样也能够产生大量的载流子,使PN结的反向电流急剧增大,最终呈现反向击穿的现象。
一般来说,PN结的击穿电压小于5V的击穿机制属于齐纳效应,大于7V的击穿机制属于雪崩效应,而介于5V与7V之间则两种击穿机制都有可能,甚至可能是两者的组合。
需要注意的是:这两种击穿都是可逆的。如果PN结出现反向击穿的现象,但是反向电流与反向电压的乘积没有超过PN结容许的耗散功率 P D (Power Dissipation),也就是PN结没有因为温度过高而烧毁,那么把外加反向电压降低之后,PN结仍然可以恢复到原来的状态。
我们通过金属接触面从合并的杂质半导体引出两个电极,由P区引出的电极称为阳极(Anode,A),由N区引出的电极称为阴极(Kathode/Cathode,K),二极管的基本结构及其原理图符号如图2.7所示。
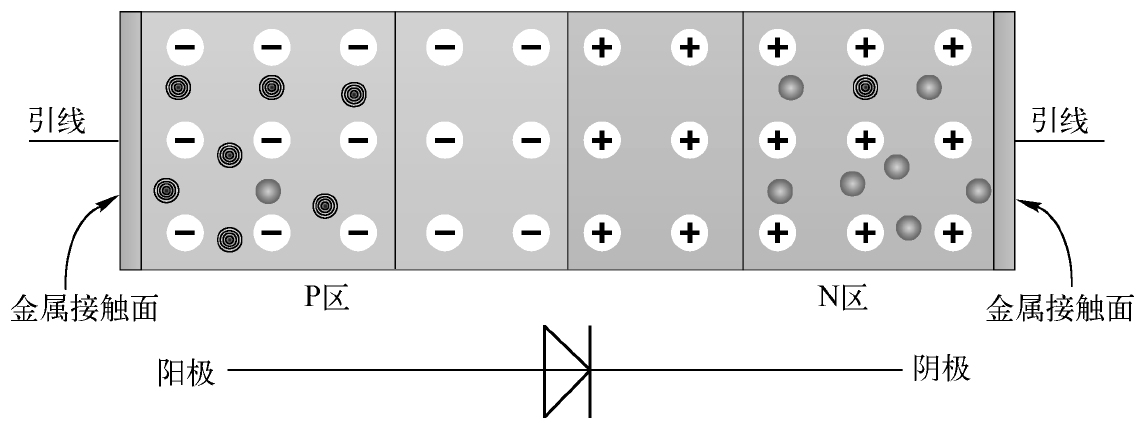
图2.7 二极管的基本结构及其原理图符号
前面讨论的给PN结施加正向与反向偏压的整个过程,可以使用图2.8所示的PN结的伏安特性曲线来表示。
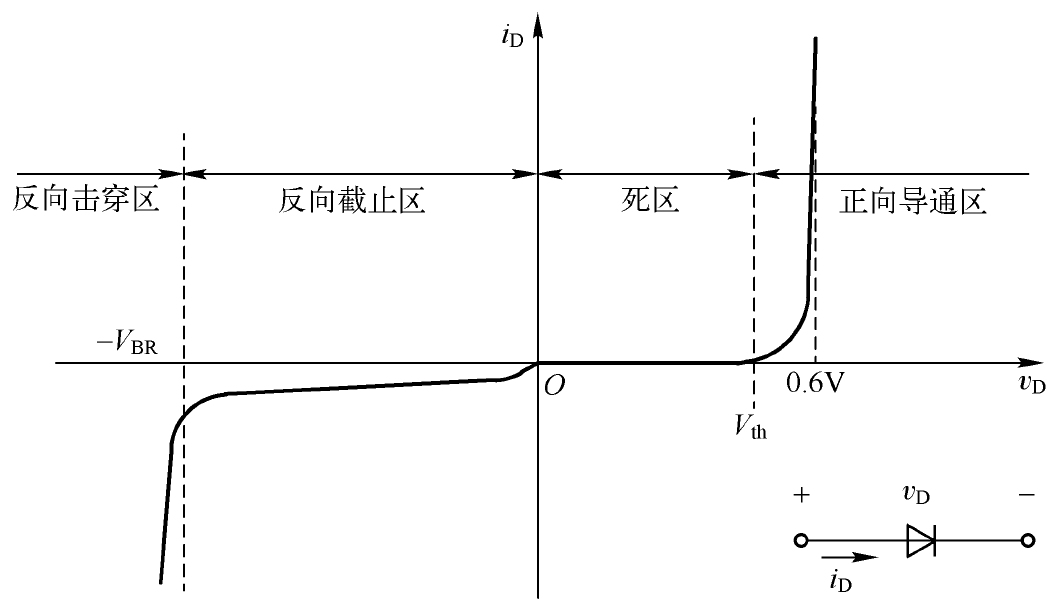
图2.8 PN结的伏安特性曲线
图2.8中, V th 表示开启电压(Threshold Voltage)或死区电压,一般硅管约为0.5V,锗管约为0.1V。当PN结两端的正向电压 v D < V th 时,外电场还不足以克服内电场对载流子的扩散运动而造成的阻力,继而使得多子不能够顺利通过空间电荷区,此时PN结呈现的电阻很大,正向电流 i D 近似为零,我们称PN结处于 截止状态 (Cut-Off State),这与在PN结两端施加反向偏压时呈现的小电流是非常相似的。当 v D > V th 时,PN结呈现的电阻很小, i D 将随 v D 的上升而上升,我们称PN结处于 导通状态 (On-State),此时PN结两端存在一定的正向导通压降,一般硅管约为0.6V,锗管约为0.2V(特殊二极管会略有不同,超过2V也是存在的)。
那反向饱和电流 I S 在哪里呢?实际上,如果把图2.8所示原点附近的曲线进行放大,会观察到如图2.9所示的原点附近的伏安特性曲线。
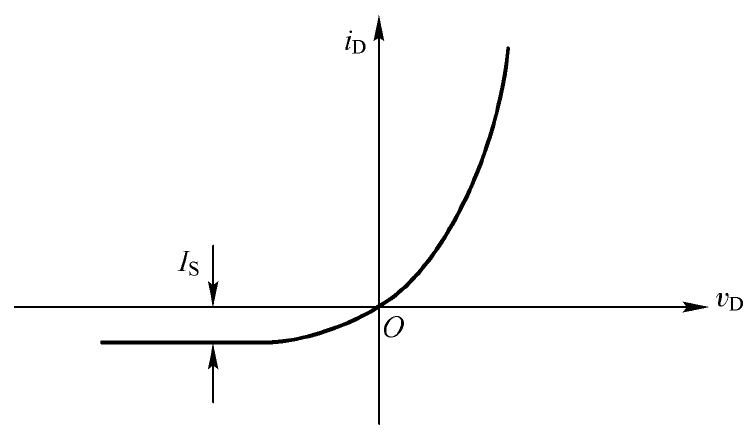
图2.9 原点附近的伏安特性曲线
在原点附近有一个反向饱和电流 I S ,其值通常在10 -1 8 ~10 -1 2 A之间,且与PN结的面积大小成正比例关系,所以也称其为比例电流(Scale Current)。而流过PN结的电流 i D 与施加在其两端的电压 v D 之间存在如下关系式:

对于一个明显的正向电流 i D ,它总会远远大于 I S ,所以式(2.2)可简化为下式:

这个式子说明 i D 与 v D 之间近似服从指数函数的关系,其中 V T 就是我们提到过的热电压。而之所以重点提到反向饱和电流,是因为它是一个非常重要的参数,后续会经常涉及。
需要特别注意的是,二极管虽然存在很小的反向电流 I R ,但仍然远比 I S 大得多, I R 多出的那部分通常由耗尽区的载流子或泄漏效应而引起,这些因素与PN结的面积大小呈正比例关系。另外, I S 与 I R 的温度特性也有所不同,前者的温度每升高5℃,其值增加约1倍,后者的温度每升高10℃其值增加约1倍。
总的来说,二极管在被施加一定的正向偏压时呈现导通状态,而被施加一定的反向偏压时呈现截止状态,这就是它的单向导电性,这种特性使得二极管在刚刚步入电路设计领域时就获得了很广泛的应用。
二极管最经典的应用莫过于将交流(Alternate Current, AC)转换为直流(Direct Current, DC),我们称该转换过程为整流(Rectifying),相应的电路称为整流电路,相应的二极管称为整流二极管。
所谓直流信号,就是大小与方向均不变的信号;而交流信号是方向与幅值的大小均发生变化的信号,如图2.10所示为直流与交流信号(脉动直流可以认为是直流与交流的叠加)。

图2.10 直流与交流信号
家里使用的很多电器(如冰箱、空调、电视机和洗衣机等)会直接使用220V的交流电,然而大多数直接控制电器运行的相关电路只有在直流供电的条件下才能正常工作,所以家用电器的内部通常都会有整流电路。如图2.11所示为基本的半波整流(Half-Wave Rectifier, HWR)仿真电路。
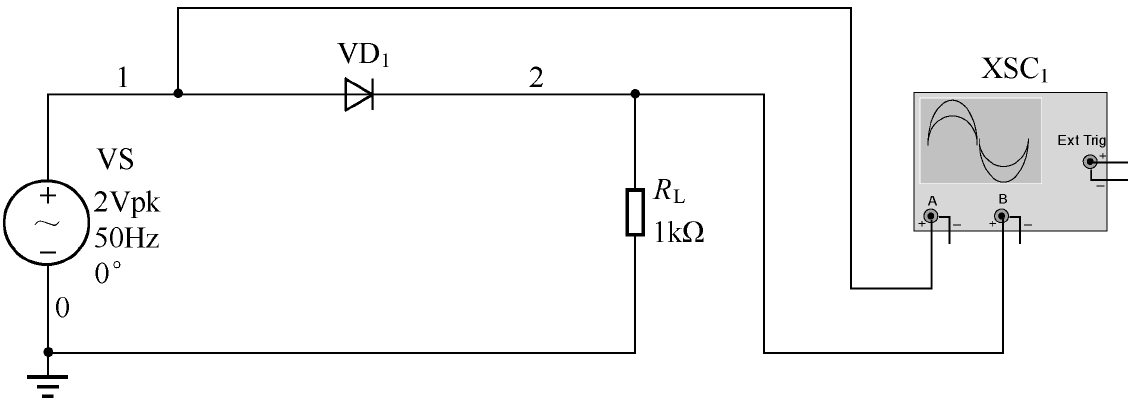
图2.11 基本的半波整流仿真电路
基本的半波整流仿真电路的结构非常简单,把整流二极管VD 1 串联在输入交流电压源VS(峰值为2V,频率为50Hz,“S”表示“Source”)与负载(Load) R L 之间即可。什么是负载呢?如牛拉车,车就相当于负载。用电设备都是消耗能源的负载,我们通常使用一个电阻 R L 来等效它。
当 v s 大于0.5V(VD 1 的死区电压)时,VD 1 处于导通状态且两端有一定的正向压降 v D ,负载 R L 的两端即可获得极性为上正下负的电压。相反,当 v s 小于0.5V时,VD 1 处于截止状态,整个回路是断开的,负载 R L 的两端没有电压,如图2.12所示为二极管的单向导通特性。
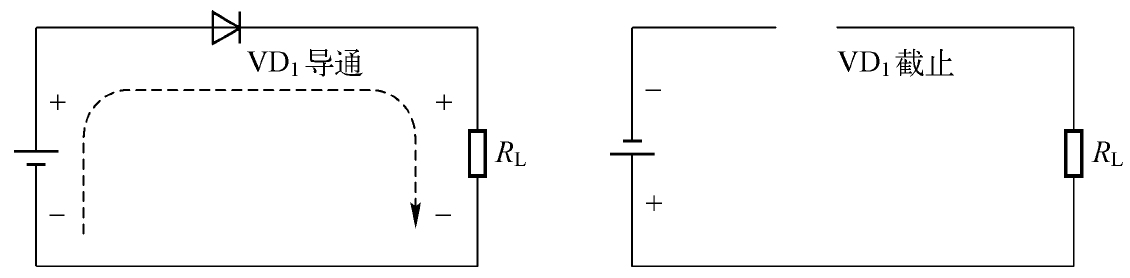
图2.12 二极管的单向导通特性
很明显, R L 的两端只有上正下负的脉动直流电压,即完成了将输入交流处理为脉动直流的功能,相应的仿真波形如图2.13所示。
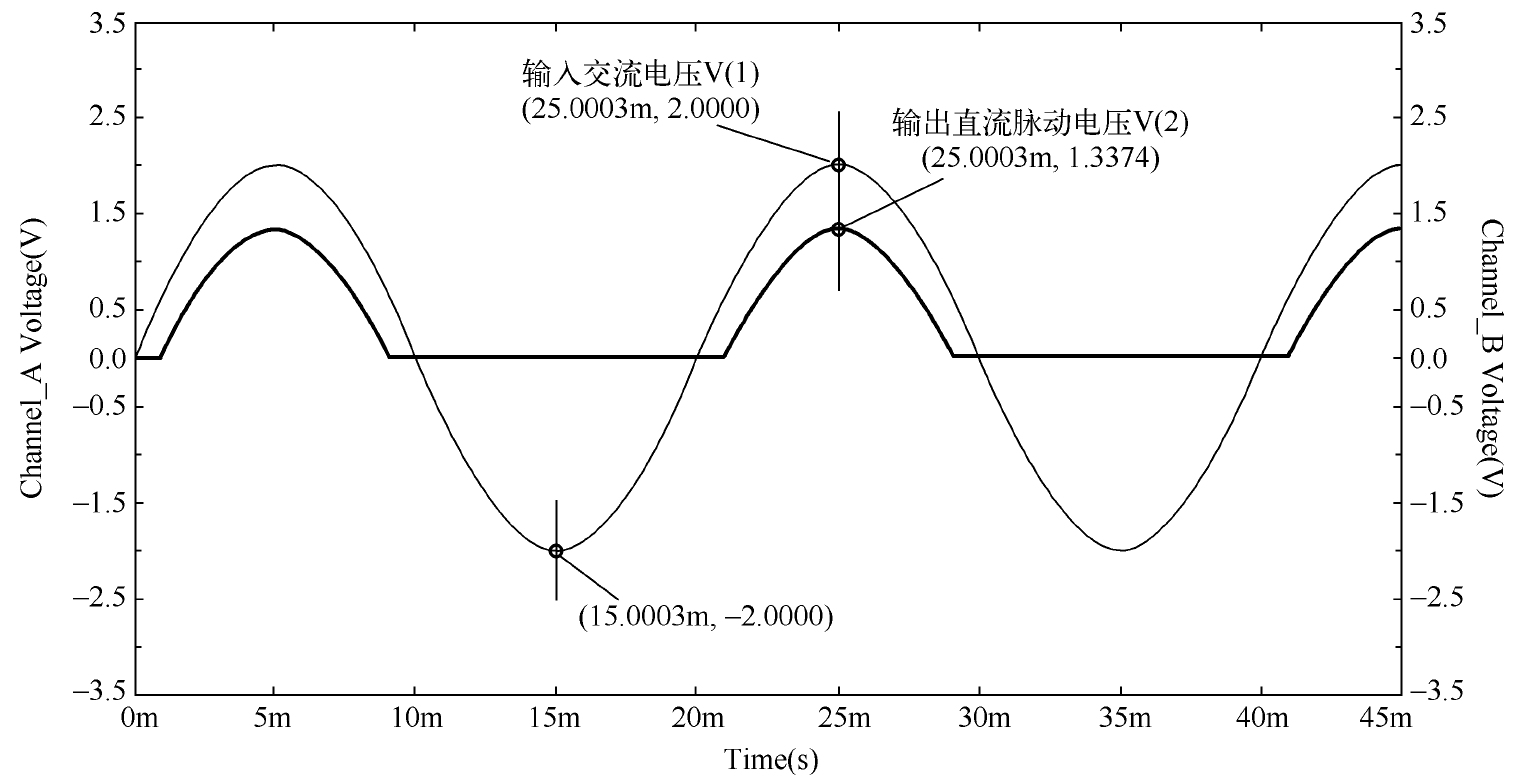
图2.13 相应的仿真波形
仿真波形中的V(1)表示节点1的电位,V(2)表示节点2的电位,这些节点与图2.11所示的仿真电路中连线旁边的数字是对应的,这也是Multisim软件平台对电路网络节点参数的标记方式,相应地也有电流I(*)和功率P(*)的标记方式。
在对半波整流电路进行仿真时,我们特意将输入信号源的峰值设置得比较小。从图2.13中可以看到,由于二极管正向导通压降的存在,输出电压的峰值比输入电压的要小约0.6V,也就是有一定的损耗。所以,这种半波整流电路在输入交流电压的峰值接近(或小于)二极管死区电压的场合中并不适用,而是使用运放与二极管构成的精密整流电路比较合适。当然,如果输入交流电压的峰值远大于二极管的死区电压(如220V的交流电),我们通常会把二极管当作理想的二极管,在这种情况下,可以忽略正向导通压降引起的误差。
半波整流电路的输出效率比较低,输入交流电压的负半周对负载 R L 完全没有能量贡献,所以另外一种效率更高的全波整流电路(Full-Wave Rectifier, FWR)应用更加广泛,如图2.14所示为全波整流电路。
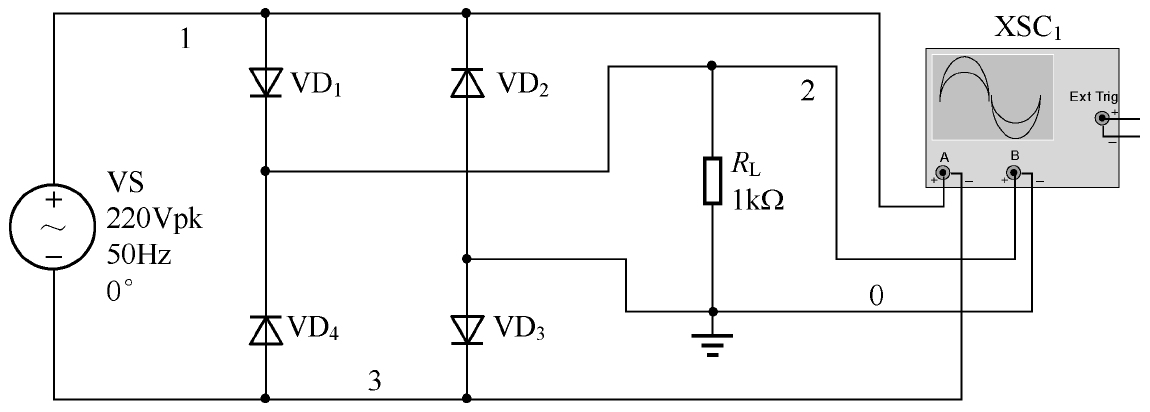
图2.14 全波整流电路
当输入交流电压的正半周到来时,VD 1 与VD 3 处于正向导通状态,负载 R L 两端电压的极性为上正下负;而当输入交流电压的负半周到来时,VD 2 与VD 4 处于正向导通状态,负载 R L 两端电压的极性为上正下负,如图2.15所示为全波整流电路的仿真波形。
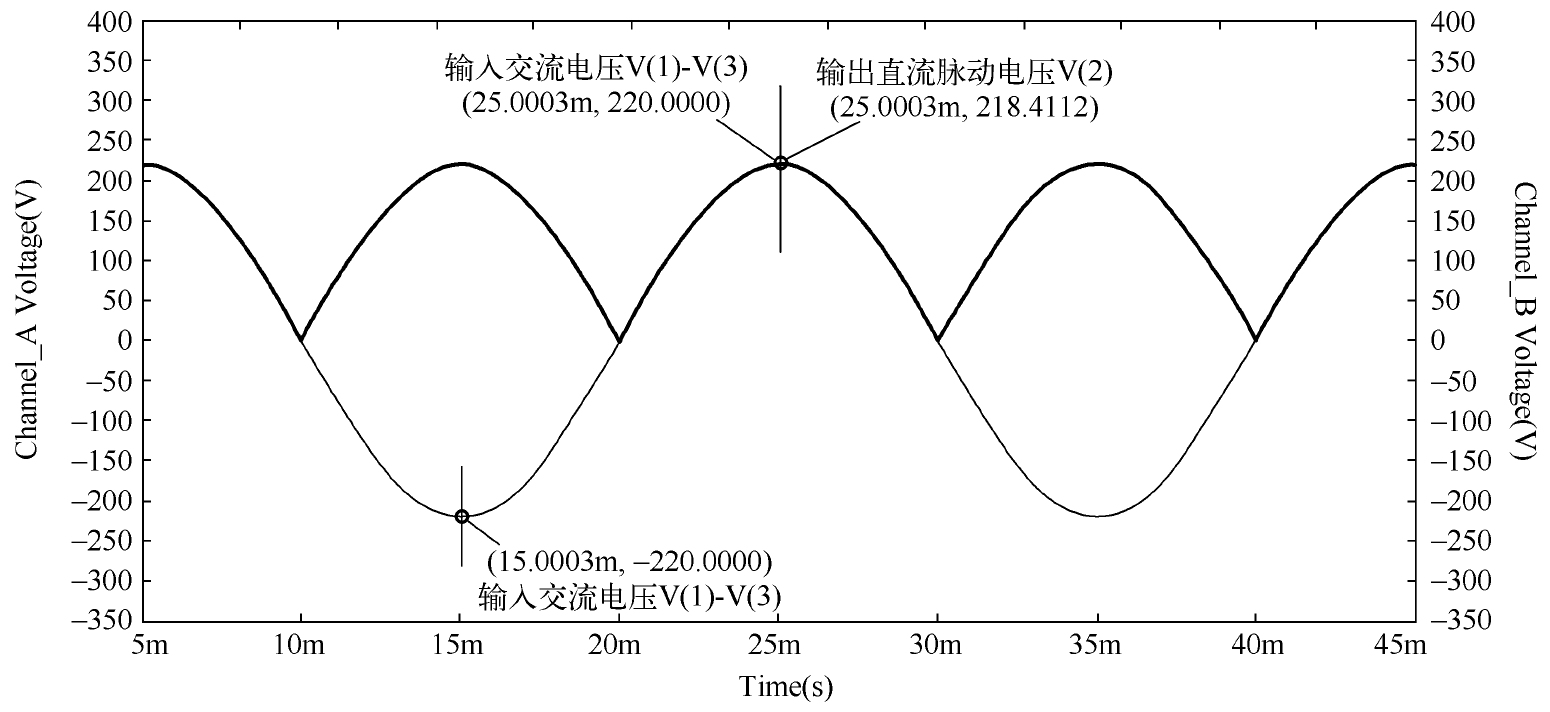
图2.15 全波整流电路的仿真波形
从图2.15中可以看到,输入与输出电压的峰值相差约两个二极管的导通压降(约1.6V),但对于峰值为220V的大电压而言,这点损耗完全可以忽略不计。很明显,全波整流电路的输出效率更高,输出电压的平均值为半波整流电路的两倍。虽然全波整流电路使用了4个二极管,相对于半波整流电路貌似成本高一些,但是现如今二极管的价格已经非常低了,而且全波整流电路对后级滤波电路的要求也低一些,所以额外使用两个二极管还是值得的。
限幅电路与钳位电路也是二极管的经典应用。限幅电路(Limiting Circuit)将输入信号的幅值限制在一定的范围内,以避免因电压过大而损坏某些元器件。我们先看一个简单的限幅仿真电路,如图2.16所示。
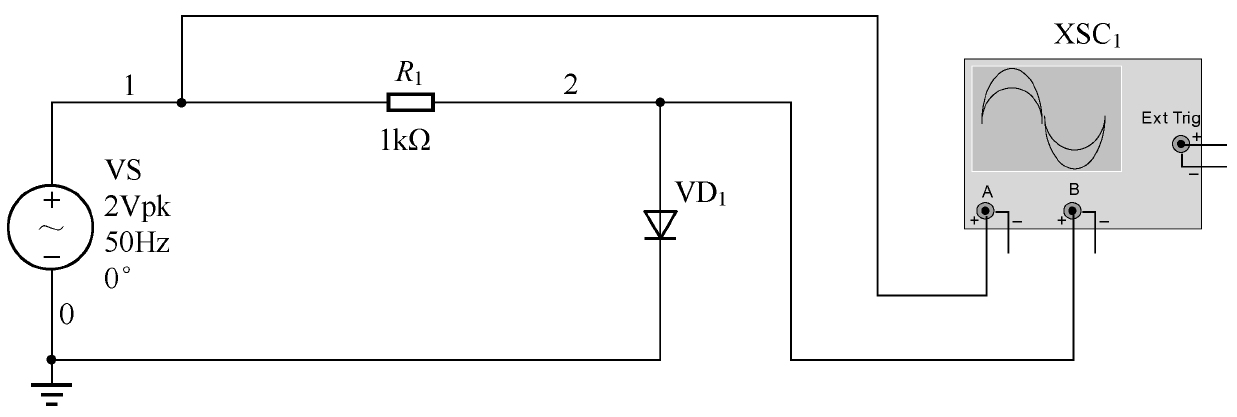
图2.16 限幅仿真电路
当输入信号的电压小于0.5V时,VD 1 截止,此时回路是不导通的,输出信号等于输入信号;当输入信号的电压大于0.5V时,处于导通状态的VD 1 会将输出电压限制为一个二极管正向导通的压降(约为0.6V),如图2.17所示为限幅电路的仿真波形。
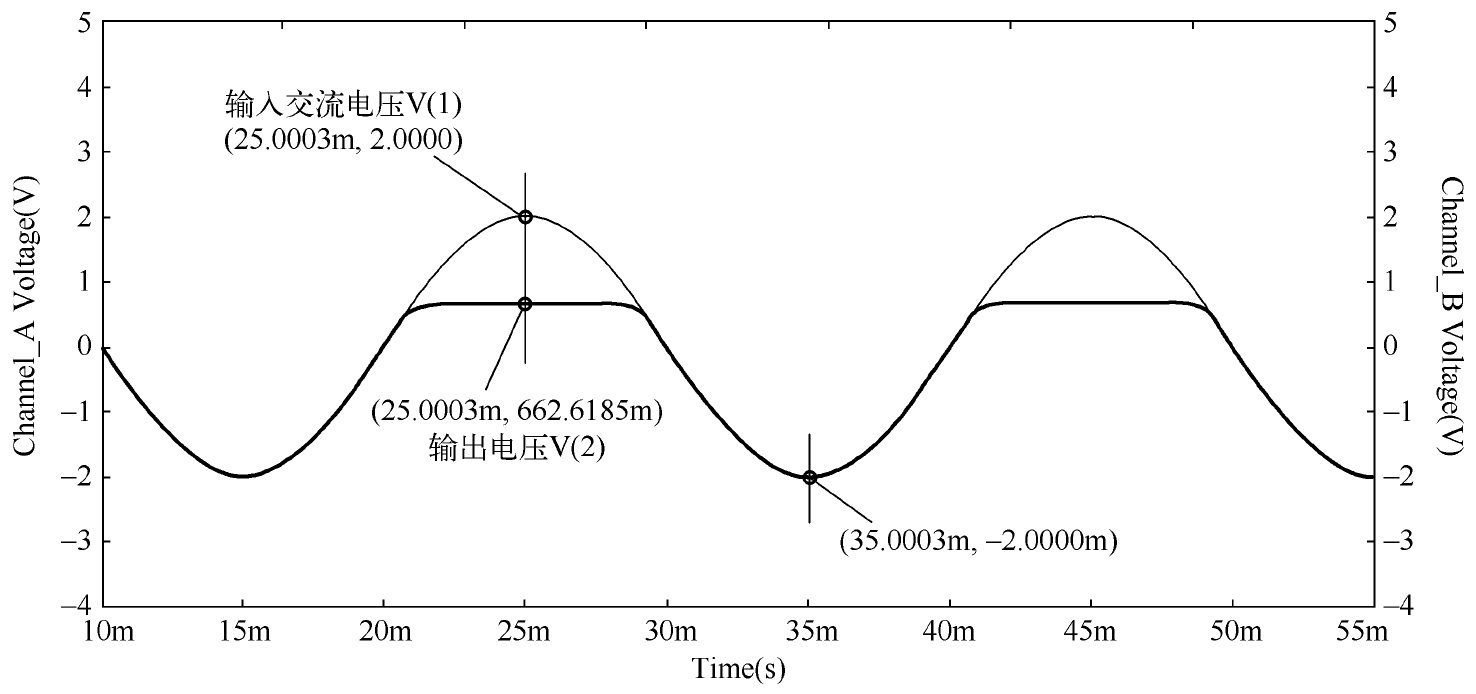
图2.17 限幅电路的仿真波形
当然,限幅电路具体的变化形式有很多,如可以通过串入多个二极管(或直流电源)调节需要限制的信号幅度,也可以将二极管的极性反过来连接来限制负半周的信号幅度,还可以使用反向并联的二极管同时限制正负半周的信号幅度,甚至可以将多种方式混合应用,如图2.18所示为各种不同的限幅电路。
钳位电路(Clamping Circuit)能够将输入电压偏移到另一个不同的电压值上,最简单的钳位仿真电路如图2.19所示。
假设初始状态下的输入电压为-10V,此时VD 1 导通并对电容 C 1 快速充满电(极性为左负右正),而输出电压仅比公共地(0V)低一个二极管压降。当输入电压跳变为+10V时,由于电容两端的电压不能突变,它与输入电压串联形成+20V的输出电压,此时VD 1 是截止的,只要 R L 的阻值不是很小(电容放电的速度很慢),在输入电压再次跳变为-10V之前,我们可以认为电容两端的压降是不变的,最简单的钳位仿真电路的仿真波形如图2.20所示。
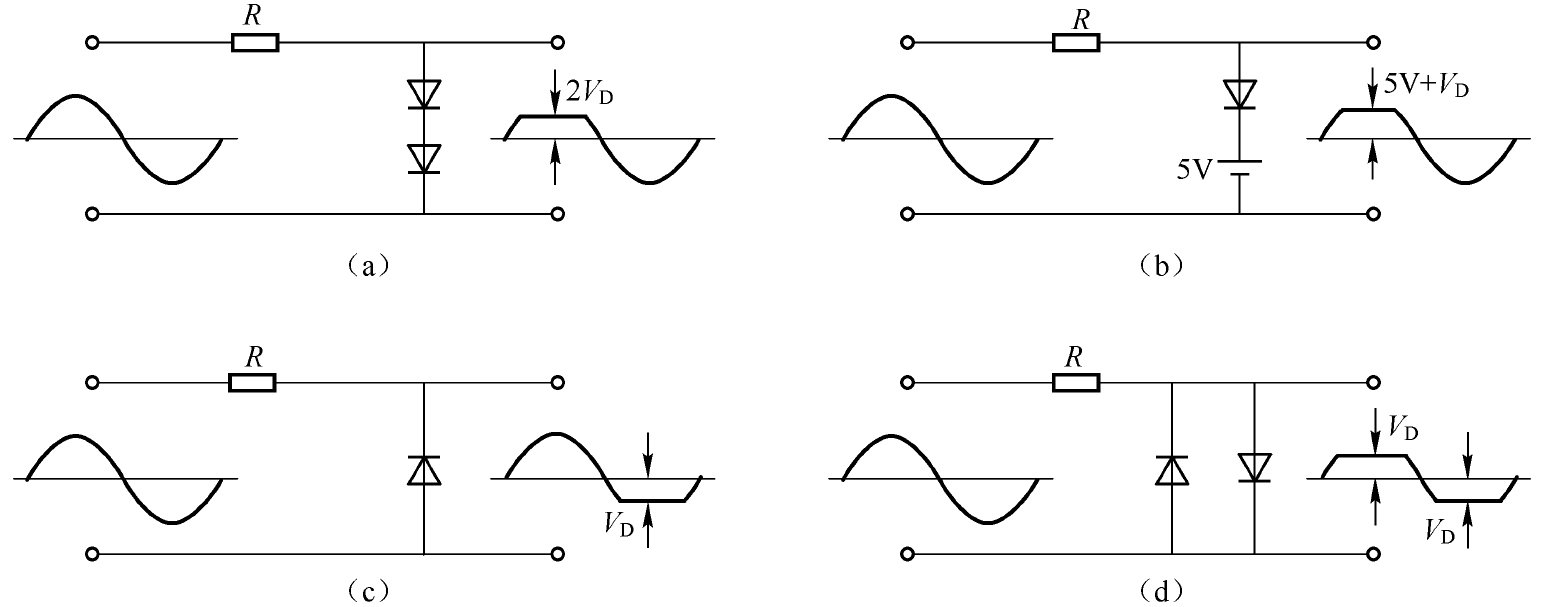
图2.18 各种不同的限幅电路
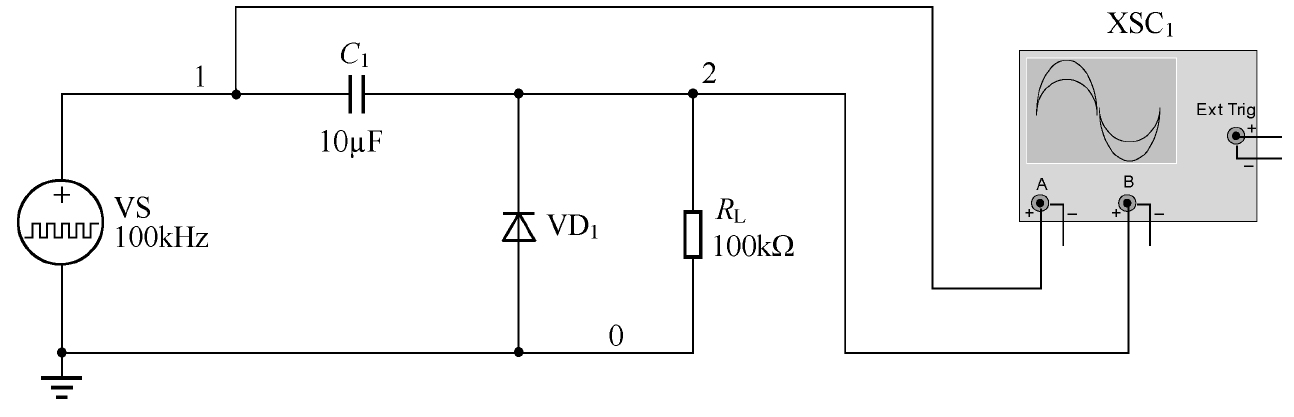
图2.19 最简单的钳位仿真电路
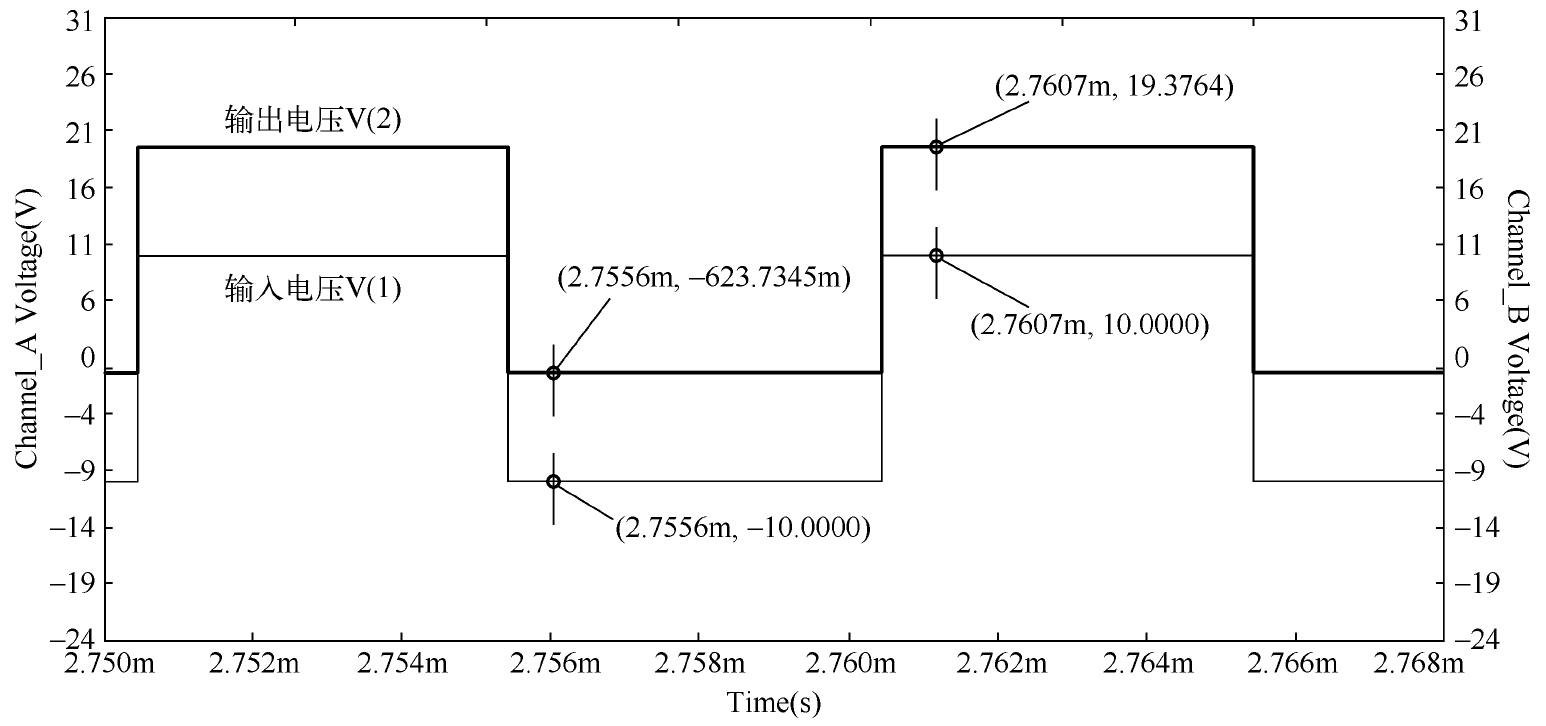
图2.20 最简单的钳位仿真电路的仿真波形
与限幅电路相似,钳位电路也有很多形式,如用二极管串联直流电源来调节波形偏移的程度,本文这里不再赘述。需要指出的是,很多读者容易混淆限幅电路与钳位电路,它们两者的区别是 前者削掉输入信号的一部分而对剩余部分不做任何改变,后者对信号不做改变而仅进行一定数值的偏移。
以上讨论的是普通二极管的应用,它们都是利用其单向导电特性来实现的。实际上还有一些重要的特殊二极管值得我们注意,如稳压二极管(简称“稳压管”)就是其中之一,也称为齐纳二极管(Zener Diode),这是以早期从事该领域的一位科学家的名字命名的,稳压二极管的原理图符号如图2.21所示。
图2.21 稳压二极管的原理图符号
稳压管是一种使用特殊工艺制造的面结合型硅半导体二极管,在实际应用时处于 反向击穿状态 (外加电压的正端与阴极连接,负端与阳极连接),其典型的应用电路如图2.22所示。
稳压管与电阻串联就构成了最简单的稳压电路。需要特别注意的是: 输入电压是反向施加在稳压管两端的。 电阻 R 1 用来限制流过稳压管中的电流(以避免消耗的功率过大导致温度过高而被损坏),所以也称为限流电阻。稳压管之所以能够稳定电压,是因为它在击穿区域具有非常陡峭的伏安特性曲线,如图2.23所示为其击穿区域的伏安特性曲线。
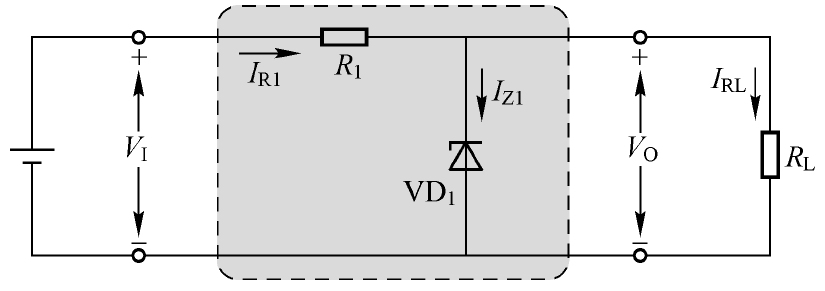
图2.22 稳压管典型的应用电路
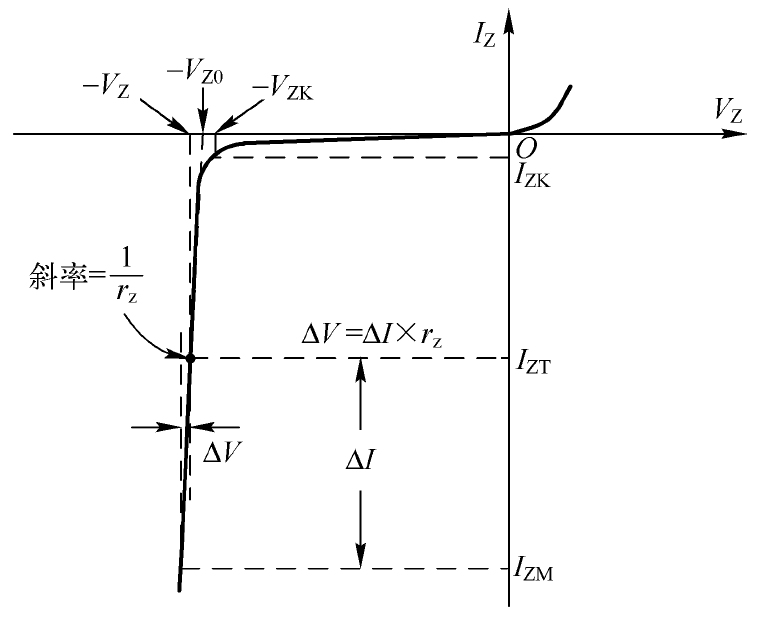
图2.23 稳压管击穿区域的伏安特性曲线
从图2.23中可以看到,只要稳压管两端的压降发生很小的变化(∆ V ),就会使流过的电流发生很大的变化(∆ I ),这个特点可以解释稳压电路的工作原理。当输入电压 V I 上升的时候,理论上输出电压 V O (稳压管两端的压降)也会上升。但是,稳压管两端电压的上升量即便很小,流过其中的电流 I Z1 也会急剧上升。这样,流过 R 1 的电流就会急剧上升,从而使 R 1 两端的压降急剧增加。最终导致的结果是:虽然输入电压上升的变化量比较大,但是 R 1 把大多数电压上升的变化量分担了,而稳压管两端压降的变化量却比较小,从而达到稳定输出电压的目的,这个稳压过程可表示为
V I ↑→ V O ↑→ I Z1 ↑↑→ I R1 ↑↑→ V R1 ↑↑→ V O ↓
当负载 R L 的阻值下降的时候,负载电流 I RL 就会增加,理论上输出电压应该也会下降,但是只要稳压管两端的压降下降一点点,流过其中的电流 I Z1 的下降量反而会更大。由于此时的输入电压是不变的,所以流过 R 1 的电流也基本不变。虽然 I RL 增加了,但是 I Z1 却下降了,输出电压仍然还是稳定的。也就是说, I RL 的上升量来自 I Z1 的下降量,这个稳压过程可表示为
R L ↓→ I RL ↑→ V O ↓→ I Z1 ↓↓( I R1 不变)→ V O ↑
从稳压过程中可以看到,这种稳压电路是利用稳压管电流的自动调节原理来满足负载电流的改变的,然后与限流电阻 R 1 配合,把输入电压的变化转换成 R 1 两端压降的变化,而输出电压却可以几乎保持不变。
在对稳压电路进行设计时,需要特别注意限流电阻的取值范围,从而保证稳压电路在最坏的条件下也能够正常工作。那怎么样才算稳压电路正常工作呢?我们从图2.23中可以看到 I ZK 与 I ZM 两个参数,其中 I ZK 是稳压管能够进入稳压状态的最小电流,称为膝点或拐点电流(Knee Point Current),所以限流电阻不宜过大,否则稳压管将退出反向击穿状态,这样也就不再有稳定电压的能力了。当然,限流电阻也不宜过小,以避免稳压管因流过的电流 I Z1 超过最大稳定电流 I ZM ,导致消耗的功率过大而被损坏,所以使稳压管正常工作的电流 I Z1 的范围为
I ZK <I Z1 <I ZM (2.4)
我们可以根据两种最坏的条件进一步推导出限流电阻的计算公式。第一种情况,当输入电压最大且负载电阻也最大(负载电流 I RL 最小)时,流过稳压管的电流 I Z1 = I R1 - I RL 为最大值,此时要保证 I Z1 <I ZM ,所以有:
I R1 - I RL <I ZM (2.5)
I R1 可由输入电压减去输出电压后再除 R 1 获得, I RL 则为输出电压除负载电阻 R L ,即有:

整理一下,可得到 R 1 最小值的表达式,即

再来看第二种情况,当输入电压最小且负载电阻最小时,流过稳压管中的电流 I Z1 为最小值,此时要保证 I Z1 >I ZK ,同样展开之后再整理一下就可以得到 R 1 最大值的表达式,即

我们举一个简单的电路设计实例: 在图2.22所示的电路中,假设输入电压为12V,当输出电压等于5V时,从表2.1所示的数据手册中选择相应的稳压管,并计算当输入电压的变化范围是±10%,负载电阻 R L 在0.5~1.5kΩ之间变化时,限流电阻 R 1 的取值范围。
表2.1 1N47系列的稳压管的数据手册(部分)
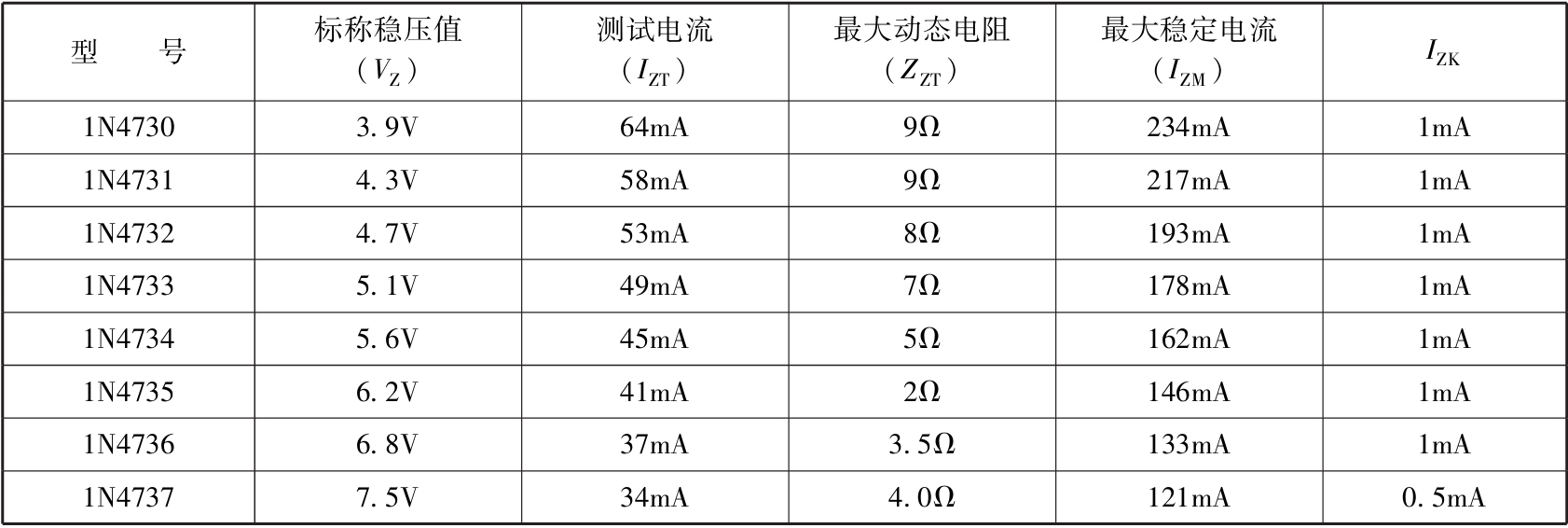
注:如非特别说明, T A =25℃。
顺便提一下, I ZT 是由1/4功率等级时定义的电流,它与稳压管的额定功耗 P Z 有如下关系:
P Z =4 V Z I ZT (2.9)
例如,1N47系列稳压管的标称功耗为1W,当标称稳压值为5.1V时,其相应的 I ZT 如下:
I ZT = P Z /4 V Z =1W/(4×5.1V)≈49mA
实际上,本例也可以使用功耗更小的稳压管(如500mW的1N46系列),但是找了很多数据手册都没有 I ZK 的值,取而代之的是一个比较小的 I ZT 的值(250μA)。此时,在这种情况下,只需要在 I ZT 的基础上留些设计裕量即可确定 I ZK 的值(如1mA)。
言归正传,既然我们需要5V的输出电压,那么理论上应该选择标称值为5V的稳压管,但是数据手册中没有5.0V的稳压管,因为稳压管本身是不能做精密稳压的,它是有一定的偏差的。实际上,数据手册也暗示了此种稳压管的精度,如选择5.1V,那么在实际工作的时候,它可能会是5.0V,也有可能是5.2V,有些数据手册会直接标出在某个测试电流下标称稳压值的最大值与最小值,一般10%和5%的精度是比较常用的。当然,也有2%和1%的精度。
我们可以选择一个略大于5V的稳压管,如5.1V的1N4733,它的最大稳定电流 I ZM =178mA。那这个电流够不够用呢?我们使用标称稳压值除以负载电阻的最小值,估算一下负载电流的最大值,即5.1V/0.5kΩ≈10mA,所以178mA也是足够的。
另外,数据手册中还有一个最大动态电阻 Z ZT (对应图2.23中的 r Z ,其定义为∆ V/ ∆ I ),其值一般在几欧姆到几十欧姆之间。此值越小,表示稳压管的稳压能力相对要好一些。为了阐述动态电阻对稳压能力的影响,我们可以把稳压管看作一个直流电源 V Z0 与动态电阻 Z ZT 的串联,那么将图2.22所示的电路可以等效为如图2.24所示的电路。
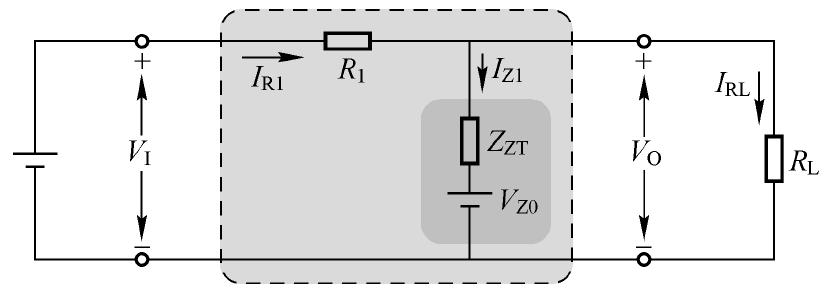
图2.24 硅稳压电路的等效电路
图2.24中, V Z0 是图2.23中斜率为1/ r Z (1/ Z ZT )的直线与横轴电压的相交点。从图2.24所示的等效电路很容易理解动态电阻对稳压能力的影响。很明显, Z ZT 越小,相同的电流变化量引起 Z ZT 两端压降的变化就会越小,输出电压也就越稳定。如果你手中稳压管的种类比较多,则可以选一个动态电阻比较小的稳压管。
接下来确定限流电阻的取值范围。由于负载电阻的变化范围是已知的,所以我们只需要计算一下输入电压的变化范围就可以了,即 V Imin =12V×(1-10%)=10.8V, V Imax =12V×(1+10%)=13.2V。
至此,式(2.7)和式(2.8)中的所有参数都是已知的,即有:
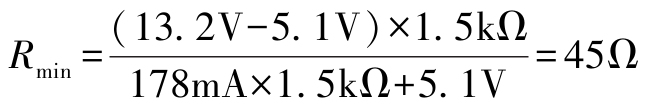
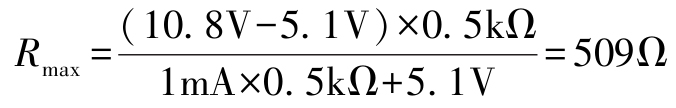
我们取一个中间值(220Ω)就可以了。在允许的范围内可以取一个比较大点的阻值,这样稳压性能也相对更好一些,同时也可以节约一些电能,环保还是要考虑的。
最后还可以计算出限流电阻消耗的功率,即
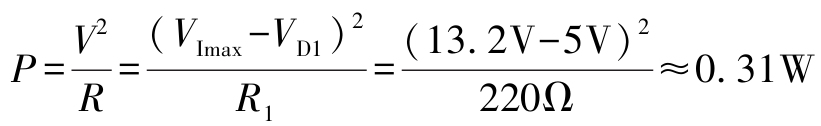
在考虑到设计裕量的情况下,我们可以选择耗散功率为1W的电阻。稳压电路的设计至此大功告成。
当然,并不是所有的二极管都是由两种类型的杂质半导体合并而成的,肖特基二极管就是一例外,其全名为肖特基势垒二极管(Schottky Barrier Diode, SBD),它是通过金属与中度掺杂的N型半导体材料接触而成的,其基本结构与原理图符号如图2.25所示。
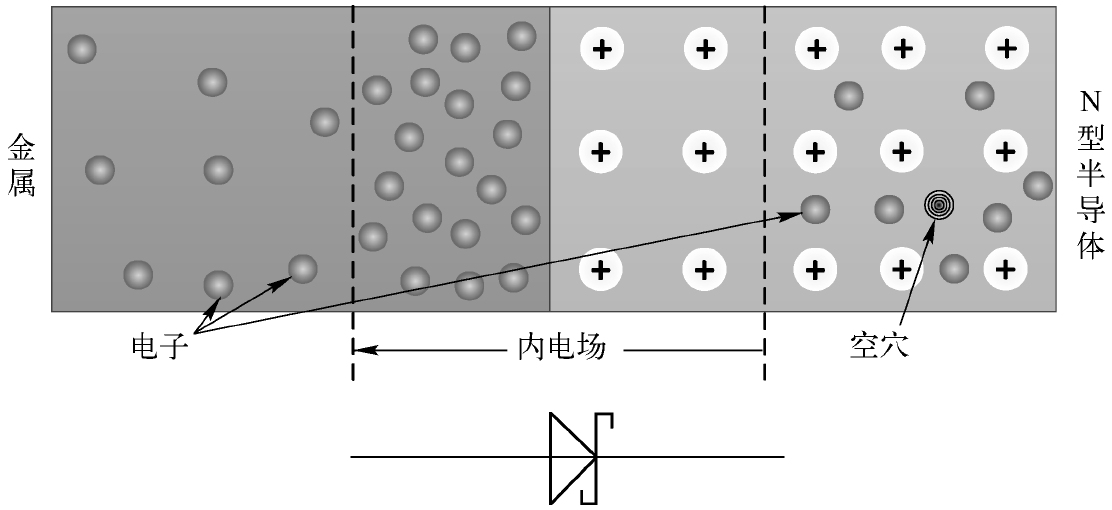
图2.25 肖特基二极管的基本结构与原理图符号
当金属与N型半导体结合时,由于金属的自由电子相对较少,从而存在浓度差,电子将从N型半导体向金属扩散。但是,金属是不存在空穴的,N型半导体得不到空穴补充而带正电,金属多了电子所以带负电,这样就形成了一个从N型半导体指向金属侧的内电场,我们称之为势垒(不能称之为PN结),它也具有单向导电性。
SBD的伏安特性非常类似于PN结二极管的伏安特性,但是相对于后者,SBD有两个非常重要的特点:其一是正向导通压降更低,由硅制成的SBD的正向导通压降一般为0.3V左右;其二是从导通转换为截止(或截止转换为导通)的速度比PN结二极管要快很多。正是这两个特点,使得SBD在某些应用场合具有很大的优势,之后在适当的时候还会对其进行进一步的讨论。
另外,发光二极管、变容二极管和光电二极管等特殊二极管也很常用,这里就不再详细讨论了,有兴趣的读者可以自行参考相关图书。最后给大家留一个小问题:既然二极管的空间电荷区存在内建电位差,那么是不是可以将多个二极管串联起来点亮小灯泡呢(见图2.26)?
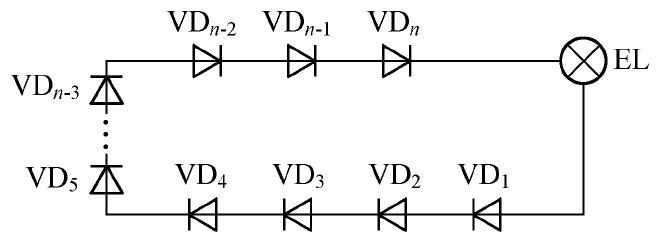
图2.26 灯泡能点亮吗