




增长率是资料分析的必考考点,首先我们需要知道如何快速的判断出一道题目要求增长率.求增长率的题目,一般有几个特征:①出现两个不同的时间相比、两个不同的年份相比、同比增长x%、环比增长x%、增长x%、减少x%、上升、下降、增长率、增速、增幅等关键词.②备选项一般为百分数或倍数(增长率大于100%时通常表示为倍数).看到这些关键词,要注意看是否要求增长率或增长率变化趋势.还要注意看清给出的基期和报告期,是不隔年(今年与去年相比,题目要求2005年,资料给出2006年数据),还是隔年(今年与前年相比,题目要求2004年,资料给出2006年数据)。
增长速度则是反映社会经济现象增长快慢程度的相对指标,它是“报告期增长量”与“基期发展水平”之比.其计算公式为:

(1)常考题型1:直接计算某一年的增长率
【例1】今年进口260亿元,去年进口180亿元,今年比去年增长百分之几?
公式:
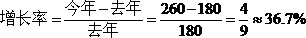
【例2】(2013国考)2006年,全国收缴土地面积1.16万公顷,……2011年,全国收缴土地面积0.38万公顷。
与2006年相比,2011年全国收缴土地面积约减少了:
A.52%
B.110%
C.67%
D.205%
【解析】公式:

故本题答案为C项。
【例3】(2012联考)2006年至2011年全年我国农村居民人均纯收入分别为3587元、4140元、4761元、5153元、5919元、6977元;城镇居民人均可支配收入分别为11759元、13786元、15781元、17175元、19109元、21810元。
2011年我国城镇居民人均可支配收入比2008年大约增加了( )。
A.18%
B.38%
C.58%
D.85%
【解析】公式:

可判定答案为B项。
(2)常考题型2:按照题目规定的标准(x%)判断增长率超过标准(达不到标准)的年份有几个?
【例1】(2015国考)
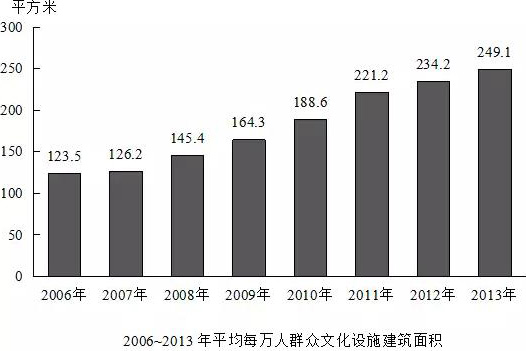
2007~2013年间,平均每万人群众文化设施建筑面积同比增速高于10%的年份有几个?
A.5
B.4
C.3
D.2
【解析】
方法一:题目要求“同比增速高于10%”,就可以将“(基期值+基期值×10%)”与“本期值”比较大小,“本期值>(基期值+基期值×10%)”的年份就符合题意.如:2006年123.5,增长10%正好为123.5+12.35=135+,2007年为126.2,故2007年同比增长率小于10%;2007年126.2,增长10%正好为126.2+12.62=138+,2008年为145.4,故2008年增长率大于10%.各年按照这种方法验证,最终答案为B项。
方法二:用增长率公式计算增长率,看增长率是否大于10%;
2007年增长率:

2008年增长率:

2009年增长率:

2010年增长率:

2011年增长率:

2012年增长率:

2013年增长率:

估算可知2008、2009、2010、2011年符合题意.故本题答案为B项。
(3)常考题型3:估算同比增速(增长率),并比较各年增长率大小,找出增速最快的、最慢的(增长率最大、最小的)
【例1】(2014国考)
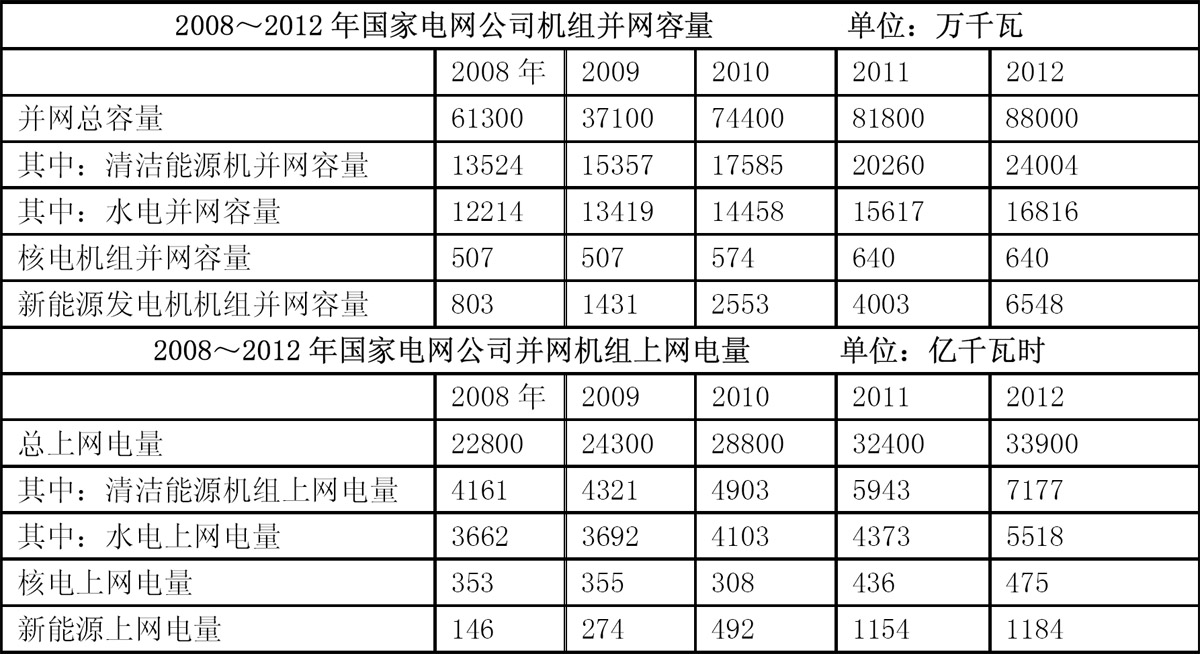
问:下列年份中,国家电网公司并网机组总上网电量同比增速最快的是:
A.2012年
B.2011年
C.2010年
D.2009年
【解析】本题考查估算同比增速并比较大小.各年国家电网公司并网机组总上网电量同比增速如下:
2012年同比增长率=(33900-32400)÷32400=15/324;
2011年同比增长率=(32400-28800)÷28800=36/288;
2010年同比增长率=(28800-24300)÷24300=45/243;
2009年同比增长率=(24300-22800)÷22800=15/228;
使用估算法,两两对比,去小留大,2011大于2012,淘汰A;2010大于2009,淘汰D;
再比较2010和2011,2010的分子大于2011的分子,2010的分母小于2011的分母,明显2010年增长率最大,应选择C.故本题答案选C。
“超计划的X%”的计算公式:
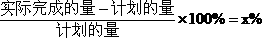
例如:计划出口l60亿元,实际完成出口190亿元,超计划的百分之几?
就是:
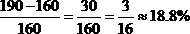
根据上面的增长速度和发展速度的计算公式可推出下面两个公式:
增长速度=发展速度-1
发展速度=增长速度+1
计算结果若是正值,则叫增长速度,也可叫增长率;若是负值,则叫降低速度,也可叫降低率.例如:某地固定资产投资1994年为366亿元,1993年为328亿元,1994年与1993年比,增长速度为(366-328)÷328=0.12,用百分数表示为12%.即1994年比1993年增长了12%或0.12倍。
增长速度由于采用的基期不同,可分为环比增长速度、同比增长速度和定基增长速度.环比增长速度是报告期水平相对上一期水平的增长速度.同比增长速度是报告期水平相对历史同期水平的增长速度.定基增长速度是报告期相对某一个固定的基期的增长速度。
例如,2002年某金融机构的存款余额15000亿元,2001年该金融机构的存款余额12000亿元,1997年该金融机构的存款余额9000亿元。
2002年存款余额的环比增长速度=(15000-12000)÷12000=25%
2002年存款余额相对1997年的定基增长速度=(15000-9000)÷9000=66.67%
我们竭诚为读者提供后续的咨询答疑服务.提供配套视频教程.化龙池公考网.联系扣扣:一八八五六五八二五;微信:一八九七五二五九二九零。
【例1】下表表示某国2006、2007、2008三年GDP变化情况:
某国2008年GDP为1500亿元,比上年增长了20%,增速比上年降低了5个百分点。

请问该国2006年GDP为多少?
【解析】
(1)思路一,分步计算:
2007年的增长率r=20%+5%=25%
2007年的GDP为Y=1500÷(1+20%)=1250
2006年的GDP为X=Y÷(1+r)=1250÷(1+25%)=1000
(2)思路二,一步计算:
求2006年GDP,如果直接列式计算就是:
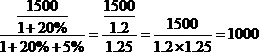
上例演示的这个简单的倒推两年的计算过程就是“三角上溯模型”.这个过程看似简单,但在资料分析中非常实用,希望各位考生对这个计算模型烂熟于心。
【例2】(2008年黑龙江真题)据统计,2007年1~8月份黑龙江省对俄贸易进出口实现69.8亿美元,增长72.3%,高于全国对俄进出口增幅31.1个百分点,占黑龙江省对外贸易进出口总值的63.1%,占全国对俄贸易进出口总值的23.2%.其中对俄出口52.5亿美元,增长95.1%,高于全国对俄出口增速13.9个百分点,占黑龙江省对外贸易出口总值的69%,占全国对俄贸易出口总值的30.9%;对俄进口17.3亿美元,增长27.1%,高于全国对俄进口增速17.4个百分点,占黑龙江省对外贸易进口总值的50%;占全国对俄贸易进口总值的13.3%。
根据统计资料,2006年1~8月份黑龙江对俄出口总值是:
A.13.6亿美元
B.26.9亿美元
C.40.5亿美元
D.52.5亿美元
【解析】
根据“对俄出口52.5亿美元,增长95.1%”可知,2006年1~8月份黑龙江对俄出口总值为
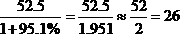 亿美元.因此,选B。
亿美元.因此,选B。
【例3】今年8月,开始于2003年的农村信用社改革第一阶段工作任务基本完成.截至今年6月末,全国农村合作金融机构(含农村信用社、农村合作银行和农村商业银行)各项贷款余额30841亿元,比改革前的2002年末增长121%;各项存款余额43394亿元,比改革前增长118%.今年上半年实现利润219亿元.全国农村合作金融机构四级分类口径的不良贷款2972亿元,不良率9.6%,分别比改革前降低了2175亿元和27.33个百分点。
问题:2002年年末全国农村信用合作金融机构各项存款余额与贷款余额相比较:
A.多12553亿元
B.少12553亿元
C.多5950.3亿元
D.少5950.3亿元
【解析】
思路一,公式计算:
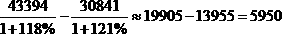 亿元,与C项最接近,因此选择C。
亿元,与C项最接近,因此选择C。
思路二,排除法:查阅资料可知“各项贷款余额30841亿元,比改革前的2002年末增长121%;各项存款余额43394亿元,比改革前增长118%”,因为43394远远大于30841,而121%与118%接近,那么200年年末存款余额一定会大于贷款余额,因此排除B、D两项。
那么A、C之中选哪一项呢?A项恰好是43394-30841=12553,考虑到计算2002年的基期量要除以“1+增长率”,那么答案绝不是12553,因此排除A,答案选C。
【例4】(2014四川)据海关统计,2011年1-9月,某省实现进出口总额293.8亿美元,比上年同期增长59.4%,增速比上年同期提升5.5个百分点,高出全国进出口增速34.8个百分点.其中,出口150.5亿美元,增长28.8%,高出全国出口增速6.1个百分点;进口143.3亿美元,增长1.1倍,高出全国进口增速85.8个百分点。
101.2009年1~9月,该省进出口总额约为多少亿美元?
A.100
B.120
C.150
D.180
【解析】本题运用三角上溯模型列式子再近似估算即可解题.对此模型熟悉了,不必列表,直接列出式子即可进行估算.掌握模型,尽量少记忆公式,减轻备考负担。
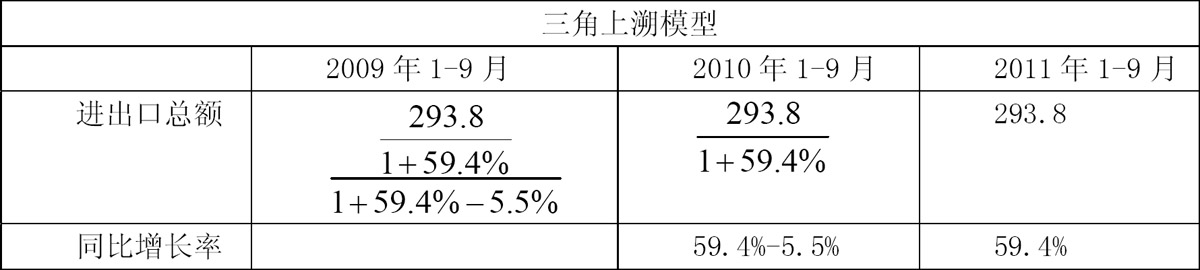
根据三角上溯模型直接列出式子:
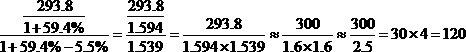
答案选B.120。
【例5】2012年,全国夏粮总产量达到12995万吨,比2011年增加356万吨,增长2.8%,超过1997年12768万吨的历史最好水平,比10年前增长31.6%。
2002年全国夏粮产量约为( )。
A.4107万吨
B.9875万吨
C.12768万吨
D.17102万吨
【解析】
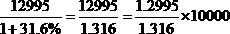 ,因为1.29小于1.32,除出来的得数会略小于1,那么答案略小于10000,因此答案选接近10000的B.答案:B。
,因为1.29小于1.32,除出来的得数会略小于1,那么答案略小于10000,因此答案选接近10000的B.答案:B。
【例6】某市2010年全年实现农业增加值124.3亿元,比上年下降1.6%.粮食播种面积22.3万公顷,比上年减少0.3万公顷;粮食产量115.7万吨,比上年下降7.3%。
该市2009年全年实现农业增加值约多少亿元?( )
A.124
B.126
C.129
D.132
【解析】根据材料中数据,2009年全年实现农业加增加值约为124.3÷(1-1.6%)≈124.3+124.3×1.6%≈124.3+2=126.3亿元.故本题答案为B项.由于本题目中增长率为负数且数值较小,可以考虑化除为乘近似公式。

求2011年相对于2009年的增长率y%?
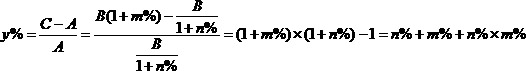

小结:我们用R表示两年混合增长率,r1表示第一年的同比增长率,r2表示第二年的同比增长率,那么: 两年混合增长率R=r1+r2+r1×r2
当r1×r2的数值较小时,忽略r1×r2,答案应当略大于R=r1+r2。
运用上面的公式做下面的题:
【例1】截至2014年12月底,全国实有各类市场主体6932.22万户,比上年增长14.35%,增速较上年同期增加4.02个百分点;注册资本(金)129.23万亿元,比上年末增长27.70%.其中,企业1819.28万户,个体工商户4984.06万户,农民专业合作社128.88万户。
截至2012年12月底,全国实有各类市场主体户数最接近以下哪个数字?
A.6100万
B.5500万
C.5100万
D.4500万
【解析】答案:B。
先利用两年混合增长率公式计算出2014比2012年的混合增长率R=14.35%+(14.35%-4.02%)+14.35%×(14.35%-4.02%)=,再用报告期值6932.22÷(1+R)。
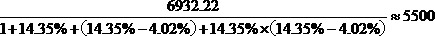
故本题答案为B项。
【例2】据海关统计,2011年1-9月,某省实现进出口总额293.8亿美元,比上年同期增长59.4%,增速比上年同期提升5.5个百分点,高出全国进出口增速34.8个百分点.其中,出口150.5亿美元,增长28.8%,高出全国出口增速6.1个百分点;进口143.3亿美元,增长1.1倍,高出全国进口增速85.8个百分点。
问:2009年1~9月,该省进出口总额约为多少亿美元?
A.100
B.120
C.150
D.180
【解析】
方法一,运用“基期值=报告期值/(1+R)”和“两年混合增长率R=r1+r2+r1×r2求R”列出式子,再估算。
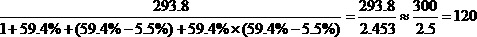
方法二,运用“三角上溯模型”列出式子,再估算。
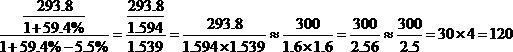
【例3】2011年1-7月,全国粗钢产量31731万吨,同比增长2.9%,增速同比下降6.4个百分点.2009年1-7月,全国粗钢产量约为多少亿吨?
A.2.0
B.2.4
C.2.8
D.3.2
【解析】思路一,根据三角上溯模型直接列式子,观察式子就可以排除A和D。
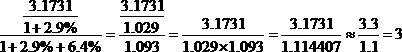
因为估算时把3.1731放大为3.3了,把1.114407缩小为1.1了,那么答案一定会略小于3,故答案选C。
思路二,2009年的增长率为2.9%,同比下降了6.4个百分点,可知2008年的增长率为9.3%,根据下面的公式

直接列式子,观察式子就可以排除A和D。
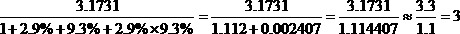
因为估算时把3.1731放大为3.3了,把1.114407缩小为1.1了,那么答案一定会略小于3,故答案选C。
【例4】(2009年北京应届真题)
2007年我国对主要国家和地区进出口额及其增长速度
(单位:亿美元)

2007年我国对韩国货物进出口总额约比上年增长:
A.15.6%
B.19.1%
C.26.1%
D.44.2%
【解析】根据题意,2007年我国对韩国进出口总额为561+1038=1599亿美元,2006年为:
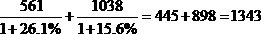
2007年我国对韩国货物进出口总额约比2006年增长
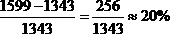 ;答案:B。
;答案:B。
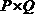 的同比增长率s=p+q+p×q;当p和q的数值很小时,p×q的数值可以忽略,答案略大于p+q;
的同比增长率s=p+q+p×q;当p和q的数值很小时,p×q的数值可以忽略,答案略大于p+q;
【例1】2010年,某省人口达到3978.75万人,同比增长7.04%,人均GDP2.75万元,同比增长8.35%,2010年,该省GDP增长了( )
A.15.49%
B.16.08%
C.16.83%
D.17.39%
【解析】GDP总值=人均GDP×人口数;人均GDP同比增长p=8.35%;
人口数同比增长q=7.04%;GDP总值增长=8.35%+7.04%+8.35%×7.04%
≈15.39%+1/12×7.04%≈16%;答案:B。
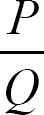 的同比增长率
的同比增长率
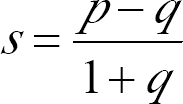
【例1】2014年,新登记注册外商投资企业3.84万户,同比增长5.76%,注册资本1796.39亿美元,同比增长23.87%.2014年,新登记注册外商投资企业户均注册资本约比上年同期增长?
A.17%
B.12%
C.8%
D.4%
【解析】户均注册资本=注册资本/户数;注册资本同比增长p=23.87%;
户数同比增长q=5.76%;户均注册资本增长率=(23.87%-5.76%)/(1+5.76%)
≈18.11/1.05≈17%;答案:A。
3.已知:P和P的同比增长率p,Q和Q的同比增长率q,那么“P+Q”混合成整体O的同比增长率
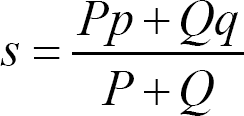 ;
;
(本项,更多解题方法和例题,见本书第3章解题方法,第十项,张氏扯平律)